레딧에서 재미있는 질문이 있었습니다(삭제되었어요). 이 질문은 텅 빈 지구의 물리학에 대해 물었습니다. 질문이 완전히 명확하지는 않았고 중요한 부분이 빠져 있었지만, 저는 답변할 거예요. 사실, 이 질문의 다른 버전을 만들어서 답변할 거에요.

중력과 고체 지구.

좋아요, 텅 빈 지구에 대해 생각해보겠지만 한 가지 중요한 것에 대해 이야기해야 해요. 중력에 대해 이야기할 거예요. 중력을 질량을 가진 물체 사이의 가 attract한 힘으로 모델링하겠어요(시간-공간 곡률로 모델링하지 않을 거예요). 이를 통해 우리는 다른 작은 물체에 의한 단위 질량 당 중력을 계산할 수 있어요. 이것을 중력장이라 하며(Newtons per kilogram 단위를 갖습니다) 벡터 g입니다.

이 작은 작은 물체로 인한 중력장은 물체의 값(m)과 그 물체로부터의 거리(r) 양쪽에 따라 달라집니다. 이것은 그 물체를 향하는 벡터이며 우리는 이를 다음과 같은 식으로 쓸 수 있습니다.

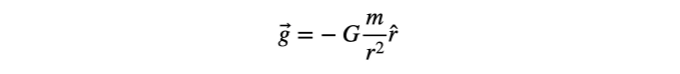
여기서 G는 값이 6.67 x 10^-11 N*m²/kg²인 범용 중력 상수입니다. 또한, r-hat가 포함되어 있음을 주목해 주세요. 만약 r이 물체에서 중력장을 찾으려는 지점까지의 벡터라면, r-hat는 전체 표현을 벡터로 만드는 단위 벡터입니다. 네, 중요합니다.

만약 점 물체가 아닌 물체가 있다면 어떻게 이 경우의 중력장 값을 찾을 수 있을까요? 마침내, 중력은 중첩 원리를 따른다는 사실이 있습니다. 이것은 하나 이상의 작은 점 물체로 인한 중력장은 각 물체의 중력장의 벡터 합이라는 것을 의미합니다. 따라서, 모든 이상한 모양의 물체에 대해 나는 그 물체를 여러 작은 물체들로 나누어 중력장을 계산할 수 있습니다.

실제 지구의 중력장을 모델링하는 데 이 아이디어를 사용해봅시다. 재밌는 건, 지구를 구성하는 1000개의 미세한 물체가 전체 지구를 1/1000만큼의 질량을 가진 것처럼 가정할 수 있다는 것이에요. 물론, 이것은 실제로는 사실이 아니에요. 지구의 밀도는 표면보다 중심에 더 높기 때문에요. 하지만, 괜찮아요 (나를 믿어봐).

우리의 지구를 나타내기 위해 5000개의 물체를 여기에 준비했어요. (네, 이건 Web VPython으로 만들었어요).

지구 표면( x축 상)에서 중력장을 찾기 위해 중첩 원리를 사용하면, g = -10.0, 0.33, -0.73 N/kg를 얻게 돼요. 9.8 N/kg의 예상치와 완전히 일치하지는 않지만, 5000개의 물체만 사용했을 때는 충분히 가까운 값이에요.

만약 지구 전체를 엄청나게 작지만 매우 질량이 많은 하나의 지점으로 대체한다면 어떨까요? 만약 이 작은 지점의 질량이 지구와 같다면, 이는 지구와 동일한 중력장 값을 만들 것입니다. 사실, 구 형태의 균일한 분포 외부의 중력장은 점 질량으로 인한 중력장과 정확히 같습니다. 이는 꽤 유용한 아이디어입니다.

이제 우리는 몇 가지 질문에 준비되었습니다.

만약 지구의 외부 10퍼센트만 남았다면 어떻게 될까요?

심지어 이것도 완벽한 질문은 아니지만 너무 길게 만들고 싶지 않았어요. 그래서, 지구 내부 일부가 마법같이 사라진다고 상상해보세요. 그 후에, 우리는 지름의 10퍼센트인 지구 바깥 부분만 남게 됩니다. 지구의 반지름이 6.37 x 10^6 미터이기 때문에 표면의 두께는 637 킬로미터가 될 것입니다.

이제 지구를 5000개의 작은 질량으로 나누는 방법은 위와 같습니다. 그러나 이러한 질량들은 지구의 외부 부분에만 있을 것입니다. 또한 이러한 모든 질량의 합은 전체 지구의 질량이 아니라 더 적은 값을 가질 것입니다.

표면 근처 물질의 밀도는 대략 3500 킬로그램/미터³입니다. 이 밀도와 남아있는 지구의 부피(남은 부분)를 이용하여 1.03 x 10²⁴ 킬로그램의 질량을 구할 수 있습니다. 네, 이는 전체 지구의 질량보다 약 20% 낮습니다.

이제 5000개의 점 질량을 만들어 봅시다. 확인해보세요.

지구 표면에서 중력장 계산을 다시 실행하니, 값이 딱 1.4 N/kg이 나왔어요. 일반적인 지구의 중력보다 훨씬 낮은 값이 나온 이유는 질량이 줄어들었기 때문이에요.

그런데 기다려봐요! 또 다른 흥미로운 상황이 생겼어요. 만약 지구 안으로 들어간다면 어떻게 될까요? 우리가 계산한 내부의 특정 위치(중심에는 아니고 중심절반 정도로)의 중력장 값은 8.88e-3, -1.46e-3, -0.22 N/kg이에요. 5000개의 질량만 사용했기 때문에 정확히는 아니지만 0에 가까울 거예요.

네, 지구 안에 들어가면 중력장이 0이 돼요. 슈퍼히어로나 붕떨어진 풍선처럼 자유롭게 움직일 수 있을 거에요(단, 공기가 있다는 전제 하에).

만약 내부를 제거하는 대신 그냥 눌러넣는다면요?

다른 방법으로는 지구를 구멍난 형태로 만들 수 있어요. 중심에 있는 물질을 모두 바깥부분으로 쫙 누르면 돼요. 이 방법의 차이점은 총 질량이 변하지 않는다는 거에요. 이 말은 지구 표면에서 중력장이 여전히 9.8 N/kg일 것이라는 거예요. 사실 대부분의 부분에서 구멍난 지구와 단단한 지구의 차이를 구별하기 어려울 거에요.

그럼, 지구가 구멍난 게 아닌 걸 어떻게 알죠?

그거 좋은 질문이에요. 지구에 대해 알아낸 거나 이게 단단한지 아니면 구멍난 것인지를 알아내는 게 참 신기해요. 표면 주변에 서서는 진짜로 알 수가 없죠. 구멍이 있는지 아니면 단단한지 알려면 속을 들여다봐야 할 텐데요 — 하지만 1킬로미터만 파봐도 멀리 못 갈 거예요. 그래서, 지구가 단단하다는 것을 시사하는 흥미로운 실험을 하나 보여드릴게요.

지구를 보기 전에 이해해야 할 중요한 개념이 몇 가지 있어요. 첫 번째로는 만유인력의 개념입니다 (이것을 방금 위에서 사용했죠). 1666년에 이삭 뉴튼은 행성이 원형으로 움직이게 하는 힘이 지구에서 물체들을 떨어뜨리는 힘과 같다고 제안했어요. 그래서 질량을 가진 두 물체는 서로 인력을 발생시켜요. 이 힘은 거리와 두 물체의 값을에 따라 달라져요.

두 번째 아이디어는 지구가 구형이라는 것입니다(그리고 평평하지 않다는 것을 바보가 아닌 사람들은 모두 알고 있었죠). 지구는 구형이며, 지구의 반지름은 에라토스테네스에 의해 결정되었습니다. 그래서 모든 사람들이 지구의 크기를 알고 있었어요.

이제 멋진 실험에 대해 이야기해 보겠습니다. 실험은 줄에 매달린 물체와 큰 산이 관련되어 있습니다. 아이디어는 마름모는 위아래로 매달리지 않고, 오히려 순수 중력장의 방향으로 매달리는 것입니다. 이 마름모를 큰 산 근처에 두면, 산으로부터 오는 중력이 측면으로 당기고 마름모에 편향을 줄 것입니다.

물체에 작용하는 세 가지 힘이 있습니다(저는 두 개만 보여줍니다). 지구로 인한 중력 힘(아래), 산으로 인한 중력 힘(측면)과 줄이 있어요. 만약 마름모의 각도를 알고 있다면, 그것이 지구로부터 오는 힘과의 상대적 중력 힘의 크기를 찾는 것은 어렵지 않습니다.

이 실험은 쉬운 것이 아닌 것 같네요. 아마도 처음으로 마주한 문제는 뭘까요 - 우리가 수직 방향을 결정하는 데 수줄기를 사용하는데, 그것의 반류를 어떻게 찾을까요. 어이쿠. 잘 찾기 힘들죠. 재밌는 점은, 별의 위치를 사용하여 수직 방향을 결정하는 것입니다.

그 다음 큰 문제는 뭘까요 - 산의 질량을 어떻게 찾을까요? 산의 밀도와 부피를 알고 있다면 질량을 찾는 것은 그리 어렵지 않습니다. 하지만 부피를 찾는 것은 정말 어렵죠. 모양이 잘 정돈된 산을 찾고 주변에 다른 산들이 그렇게 가깝지 않은 산을 찾는 것이 좋습니다 (다른 산들이 중력을 발생시킬 수 있어요).

1774년에 스코틀랜드의 산인 셸할리온 산이 선택되었습니다. 신중한 측정 덕분에, 수질기의 반류가 일상보다 작은 것을 발견했습니다. 그들은 산의 밀도가 2500 킬로그램/미터³이라는 가정으로, 지구의 밀도를 4500 kg/ m³로 계산했습니다. 참고로, 지구의 실제 밀도는 더 높습니다 - 5500 kg/m³의 값을 가지고 있어요.

하지만 이 계산을 가지고 지구의 내부에 빈 공간이 없다고 가정하는 것은 매우 어렵습니다. 지하에 있는 물질이 엄청나게 밀도가 높다는 것을 시사합니다. 훨씬 쉬운 설명은 지구가 단단한 것뿐만 아니라 지구 표면의 일반적인 바위가 아니라는 것이죠.

캐벤디시가 중력 상수(G)를 측정한 후 지구의 질량(밀도)에 대한 더 나은 값이 얻어졌지만, 이건 나중 이야기입니다. 이것이 어떻게 달성되었는지에 대한 엿보기가 여기 있습니다.