고급 데이터 과학과 금융 통찰력을 통합하여 전략적 투자 결정을 내리기

소개
본 글에서는 주식 가격을 더 정확하게 예측하기 위해 데이터 과학과 금융 분석을 결합한 방법을 소개합니다. 이번 방법에 대한 간단한 소개입니다:
트렌드 발견하기: 우리는 주식 시세를 부드럽게 만들어 트렌드를 파악하는데, cubic spline interpolation이라는 기술을 사용합니다.
주식 그룹화: 비슷한 주식들은 이러한 트렌드를 기반으로 그룹화되어, 그들을 집단으로 분석하기가 더 쉽습니다.
모델 만들기: 한 그룹을 선택하면, 우리는 미래 주식 수익을 예측하는 모델을 만듭니다.
주요 요인 설명: 우리는 SHAP 값들을 사용하여 예측에 가장 영향을 많이 주는 요인을 이해합니다.
최적 주식 선택: Response Surface Methodology (RSM)을 통해 잠재력이 높은 주식을 식별합니다.
게다가, 이 방법은 핵심 재무 개념에 대한 새로운 통찰력을 제공합니다:
시계열 한계 해결: 이 방법은 효율적 시장 가설을 고려한 안정적이고 신뢰할 수 있는 대안을 제공하여 시계열 분석의 복잡성을 탐색합니다.
샤프 비율 새로이 상상하기: 우리는 수익률 대 위험을 측정하는 방식을 개선하는 샤프 비율의 향상된 버전을 탐구합니다.
제 목표는 깊은 분석과 판단 전략을 결합하여 주식 가격을 예측하는 철저하고 효과적인 시스템을 만드는 것입니다.
데이터 수집 및 초기 정리
우선 Python을 통해 시장 데이터에 직접 액세스하기 위해 yfinance 라이브러리를 설치하세요:
pip install yfinance --upgrade
설치 후 yfinance를 사용하면 선택한 기간 동안 다양한 티커에 대한 일일 주식 가격 및 거래량을 조회할 수 있습니다:
import pandas as pd
import yfinance as yf
def get_data_by_day(ticker_list, start, end):
interval = '1d'
# 루프에서 데이터를 추가하는 것을 피하기 위해 DataFrame을 위한 열들을 미리 정의합니다
columns = ['Date', 'Open', 'High', 'Low', 'Close', 'Volume', 'ticker']
data_list = []
for ticker in ticker_list:
df = yf.download(ticker, start=start, end=end, interval=interval)
if not df.empty:
df['ticker'] = ticker
data_list.append(df)
download_data = pd.concat(data_list).reset_index()
download_data = download_data[columns] # 열 재정렬 및 관련 열 선택
unique_dates = download_data['Date'].drop_duplicates().sort_values(ascending=False).reset_index(drop=True)
date_map = pd.Series(range(1, len(unique_dates) + 1), index=unique_dates)
download_data['dayseq'] = download_data['Date'].map(date_map)
download_data = download_data.sort_values(['ticker', 'Date'], ascending=[False, False])
return download_data
데이터 수집 후: 극히 낮은 가격 또는 거래량을 가진 주식 및 음수 값으로 데이터의 정확성을 보장하기 위해 필터링하여 분석을 왜곡할 수 있는 가능성이 있는 에러를 제거합니다:
# 일관성을 위해 열 이름 조정
df = df[['ticker', 'date_dt', 'Close', 'Volume']].rename(columns={'date_dt': 'date', 'Close': 'price', 'Volume': 'Volume'})
# $1 미만의 주가를 가진 주식 제거
min_prices = df.groupby('ticker')['price'].min().reset_index()
df = df[~df.ticker.isin(min_prices[min_prices.price < 1].ticker)]
# 비양수 거래량을 갖는 주식 제거
min_volumes = df.groupby('ticker')['Volume'].min().reset_index()
df = df[~df.ticker.isin(min_volumes[min_volumes.Volume < 1].ticker)]
분석 작업을 위해 2022년 6월 7일부터 2023년 6월 7일까지 384개의 신중히 선정된 주식에 대한 데이터가 편성되었습니다. 선정 기준은 무작위가 아니며, 다양한 부문, 자산 규모, 가격 대 역까지 다양한 요소를 고려해 종합적인 시장 전체를 포착하려는 것입니다. 이 다양성을 통해 분석 결과가 전체 시장 역학을 반영할 수 있을 것으로 기대합니다.
원활한 데이터 기능을 활용한 분석 강화
분석을 개선하고 보다 정확한 예측 모델을 개발하기 위해 일일 원시 데이터 대신 원활화된 데이터를 선택했습니다. 이 방법론은 여러 가지 장점에 기반해 있습니다:
- 시장 소음 최소화: 금융 시장의 빈번한 가격 흔들림이 분석을 방해할 수 있습니다. 원활화는 이러한 변동성을 완화시켜 더 명확한 그림을 제공합니다.
· 패턴 발견: 주식 가격에 영향을 미치는 기본적인 추세를 발견하고 연구하는 것이 더 간단해집니다.
· 더 나은 군집화: 부드러운 데이터를 사용하면 유사한 가격 추세를 가지는 주식을 더 정확하게 그룹화할 수 있습니다.
· 향상된 모델링: 부드럽게 처리된 특징을 사용하면 예측 모델의 초점이 좀 더 선명해지며 효과를 증대시킬 수 있습니다.
파이썬을 사용하여 금융 데이터에 부드럽게 처리 기술을 적용하는 단계를 요약하면 다음과 같습니다:
-
데이터 분리 및 정렬: 주식 데이터를 분리하고 날짜별로 정렬합니다.
-
X 값 설정: 각 데이터 포인트를 인덱싱하기 위한 정수 시퀀스를 생성합니다.
-
Cubic Spline 적용: 가격 및 거래량 데이터에 3을 사용하여 부드러운 cubic spline interpolation을 적용하여 부드러운 곡선을 생성합니다.
-
주요 지점 선택: 이러한 곡선에서 균일 간격으로 30개의 지점을 선택하여 데이터셋을 간단화합니다.
감사합니다. 아래는 주식 데이터를 스무딩하는 파이썬 코드입니다:
# 부드럽게 정리된 데이터 저장
부드럽게 정리된 데이터를 참조할 수 있는 인덱스 열을 포함한 DataFrame에 저장합니다.
# 데이터 통합
개별 DataFrame을 통합된 데이터 세트로 병합하여 추가 분석을 수행합니다.
최종 데이터 세트는 원래 250개의 일일 데이터 포인트에서 간격이 8개의 거래일을 두고 30개의 가격 노드로 축소되었습니다.
import pandas as pd
import numpy as np
from scipy.interpolate import make_interp_spline
# 'df'이 데이터프레임으로, ['ticker', 'date', 'price', 'Volume'] 열을 가지고 있다고 가정합니다.
result_df = pd.DataFrame()
for ticker in df['ticker'].unique():
df_ticker = df[df['ticker'] == ticker].sort_values(by='date')
# x 값 생성 후 가격과 거래량에 대해 cubic spline interpolation 적용합니다.
x_vals = np.arange(len(df_ticker))
spline_price = make_interp_spline(x_vals, df_ticker['price'], k=3)(np.linspace(x_vals.min(), x_vals.max(), 300))
spline_volume = make_interp_spline(x_vals, df_ticker['Volume'], k=3)(np.linspace(x_vals.min(), x_vals.max(), 300))
# 부드러운 곡선에서 30개의 등간격 포인트를 선택합니다.
indices = np.linspace(0, 299, 30, dtype=int)
# 해당 종목의 부드럽게 처리된 데이터를 위한 DataFrame을 준비합니다.
df_smooth = pd.DataFrame({
'ticker': ticker,
'smooth_price': spline_price[indices],
'smooth_volume': spline_volume[indices],
'seq': np.arange(30, 0, -1) # 30부터 1까지 역순으로 순번을 부여합니다.
})
# 부드럽게 처리된 데이터를 추가합니다.
result_df = pd.concat([result_df, df_smooth], ignore_index=True)
여기에 AAPL을 예시로 한 부드럽게 처리된 데이터가 표시되어 있습니다:
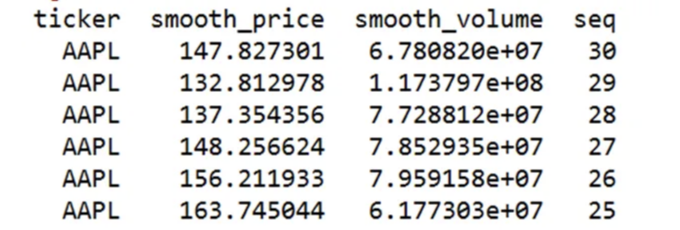
주식 군집을 통해 금융 모델을 향상시킬 수 있습니다.
시계열 모델의 도전:
ARIMA와 같은 모델로 주가를 예측하는 것은 효율적 시장 가설로 인한 도전에 직면합니다. 이 이론은 현재 주가가 모든 기존 정보를 반영하고 있어서, 시장 가격이 새로운 정보에 예측할 수 없이 반응함에 따라 예측이 랜덤 워크를 모방하게 됨을 시사합니다.
다양한 데이터의 한계:
여러 주식을 함께 모델링하는 것은 페어 트레이딩에서 사용되는 것처럼 유용한 상관 관계를 발견할 수 있습니다. 그러나 서로 다른 주식들 간의 독특한 패턴과 추세(예: AAPL 대 TSLA)는 일관된 모델 개발을 방해합니다.
전략적 접근 - 클러스터링:
주식을 행동 또는 추세의 유사성을 기반으로 클러스터로 그룹화하면 더 정확하고 그룹별 모델링이 가능해져 예측의 정확도가 향상됩니다.
KMeans를 사용한 주식 클러스터링:
- 데이터 구조화: 스무딩된 주식 데이터를 중심 가격 30개와 일치시켜야 합니다.
· 정규화: 데이터에 표준화를 적용하여 일관된 KMeans 분할을 실시합니다.
· 클러스터 최적화: KMeans 및 Elbow Method를 사용하여 이상적인 클러스터 수를 결정하고 WCSS에 초점을 맞춥니다.
· 클러스터링 평가: KMeans를 사용하여 주식을 그룹화하고 실루엣 점수를 통해 효과를 평가합니다.
여기에는 파이썬 코드가 포함되어 있습니다:
from sklearn.preprocessing import StandardScaler
from sklearn.cluster import KMeans
import pandas as pd
import matplotlib.pyplot as plt
from sklearn import metrics
# 데이터 피벗
result_df_pivoted = result_df.pivot(index='ticker', columns='seq', values=['smooth_price', 'smooth_volume'])
result_df_pivoted.columns = [f'{val}_{i}' for val, i in result_df_pivoted.columns]
result_df_pivoted.reset_index(inplace=True)
# 데이터 표준화
scaler = StandardScaler()
price_columns = [col for col in result_df_pivoted.columns if 'smooth_price' in col]
result_df_pivoted[price_columns] = scaler.fit_transform(result_df_pivoted[price_columns])
result_df_std = result_df_pivoted[['ticker'] + price_columns]
# 최적 클러스터 수 결정
K = range(1, 10)
sum_of_squared_distances = []
for k in K:
kmeans = KMeans(n_clusters=k).fit(result_df_std.drop('ticker', axis=1))
sum_of_squared_distances.append(kmeans.inertia_)
plt.plot(K, sum_of_squared_distances, 'bx-')
plt.xlabel('K values')
plt.ylabel('Sum of Squared Distances')
plt.title('Elbow Method for Optimal K')
plt.show()
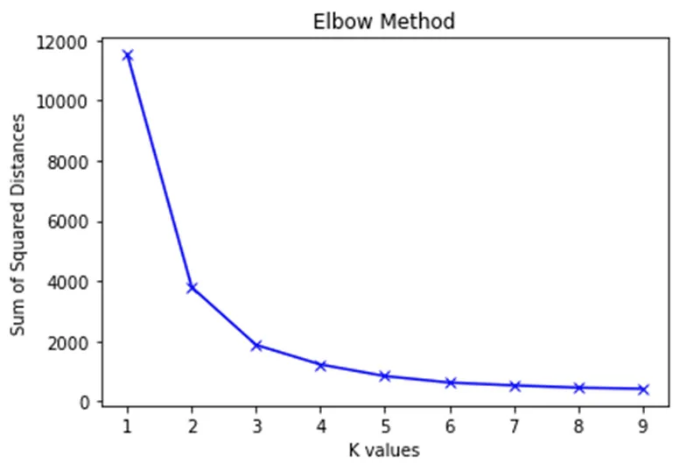
WCSS 곡선 분석 결과, 명확한 팔꿈치 지점으로 4가 최적 클러스터 수로 나타났습니다.
4개 클러스터로 진행하여, 실루엣 지수를 통해 각 클러스터의 품질을 평가합니다.
kmeans = KMeans(n_clusters=4)
result_df_std['cluster'] = kmeans.fit_predict(result_df_std.drop('ticker', axis=1))
# 성능 평가
silhouette_score = metrics.silhouette_score(result_df_std.drop(['ticker', 'cluster'], axis=1), result_df_std['cluster'])
print(f'실루엣 점수: {silhouette_score}')
실루엣 지수가 0.594로, 클러스터링 구조는 상당히 좋은 것으로 보여져 적절하게 구분된 그룹을 나타냅니다.
클러스터 분포를 시각화하기 위해 주성분 분석(PCA)를 적용하여 차원을 축소합니다:
from sklearn.decomposition import PCA
# PCA 초기화 및 X를 두 가지 구성 요소로 축소
pca = PCA(n_components=2)
X_pca = pca.fit_transform(result_df_std[cols])
# 분할별로 색칠된 PCA 변환 기능 표시
plt.figure(figsize=(10, 6))
scatter = plt.scatter(X_pca[:, 0], X_pca[:, 1], c=labels, cmap='viridis', alpha=0.75, s=7)
plt.title('주식 티커의 주성분 분석')
plt.xlabel('첫 번째 주성분')
plt.ylabel('두 번째 주성분')
plt.colorbar(scatter, label='분할')
plt.show()
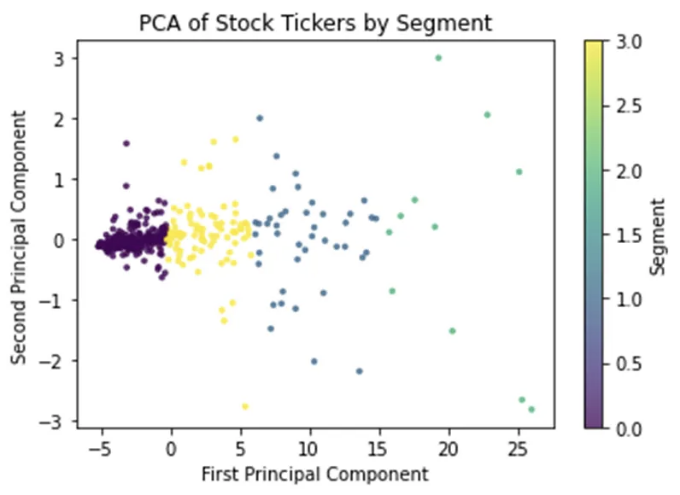
주식 가격의 동일한 행동 양식을 강조하여 주식의 명확한 그룹화를 보여주는 그림입니다.
주식 수익률 예측을 단순화하기 위한 목표 개요
목표는 식별된 클러스터 내 주식 수익률을 예측하는 모델을 개발하는 것입니다. 주요 준비 단계는 다음과 같습니다:
-
피처 선택: 이 프로젝트의 범위 내에서 오버피팅의 약간의 위험을 갖고 있지만, 다수의 피처(smooth_price1 ~ smooth_price30)를 클러스터링에 활용합니다. 더 좁은 피처 세트(smooth_price1 ~ smooth_price20)를 사용하더라도 클러스터 무결성에 큰 영향을 미치지 않습니다.
-
인구 밀집 클러스터에 집중: 모델링 노력을 인구 밀집된 클러스터에 집중하여 관찰된 패턴의 신뢰도와 일관성을 향상시키고 모델의 정밀도를 향상시킵니다.
-
모델 결과 평가: 주요 영향요인 검토와 예측 성능 평가가 포함됩니다.
샤프 지수 통합
리스크-프리 자산에 대한 투자 성과를 평가하는 데 중요한 지표인 샤프 지수는 저희 방법론의 기반이 됩니다:
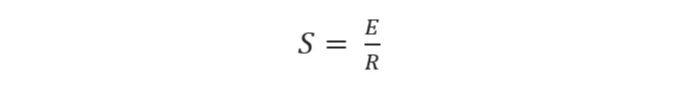
Where:
표 태그를 다음과 같이 마크다운 형식으로 변경하세요.
| S: 샤프 비율 | | E: 기대 자산 수익률과 기준 수익률의 차이 | | R: 자산 초과 수익의 표준 편차 |
선형 회귀 포함: 우리는 샤프 비율 (S)을 선형 회귀 모형에서 계수로 통합하여 주식 성과를 클러스터 내에서 평가합니다. 더 높은 비율은 우수한 결과와 관련되어 있습니다. 응용 프로그램 목적을 위해, 우리는 R로 '위험' (주식 수익의 변동성 또는 수익의 표준 편차)을 대체하고 E로 실제 주식 수익을 대체합니다.
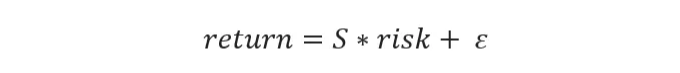
샤프 비율에 관한 맥락에서 중요한 점은 선형 회귀 모델이 예측 모델이 아닌 것을 알아야 합니다. 대신, 이 모델은 주식 수익과 위험 사이의 상관 관계를 동일한 시간 프레임 내에서 반영합니다. 더 나아가, 선형 회귀는 개별 주식의 특성에 속하는 샤프 비율을 유도하기 위해 다양한 주식 그룹에 대해 적용될 수 없습니다.
그러나 이 회귀 접근법을 다양한 주식 클러스터에 적용함으로써, 이러한 클러스터의 성능을 평가하고 차별화하는 비교적인 샤프 비율과 비슷한 특성을 생성할 수 있습니다. 이 방법은 샤프 비율을 과거 지표로 활용하여, 어떻게 투자가 위험 조정 수익 측면에서 진행되었는지를 보여줍니다.
주식 예측을 위한 샤프 비율 사용의 한계
종목 예측에 Sharpe Ratio에 의존하는 주요 과제는 다음과 같습니다:
-
복잡한 상호 작용: Sharpe Ratio와 수익의 관계는 상이할 수 있으며, 일부 주식에 대해 양의 값을 가지는 반면, 다른 주식에 대해서는 음의 값을 가질 수 있어서 단일 관점으로 캡처할 수 없는 다양한 상호 작용을 나타낼 수 있습니다.
-
불완전한 그림: 위험과 수익을 단일 측정 값으로 요약함으로써, 과거 수익 추세와 같은 중요한 요소를 놓치게 됩니다.
-
단순한 관계: 미래 수익과 단일 측정 값 간의 선형 관계를 가정하는 것은 복잡하고 비선형적인 동력을 간과하며, 이는 이차식 관계와 같은 비선형 표현에 대한 모델을 개선하고 최적화하는 것을 어렵게 합니다.
모델 강화 전략
모델을 개선함에 있어 Sharpe Ratio 개념에서 영감을 받아 한계를 극복하기 위해 다음과 같은 전략을 사용합니다:
-
향상된 피처 엔지니어링: 수익 변동성 및 과거 수익의 이차식과 같은 보다 다양한 변수를 포함하여 정밀도를 향상시킵니다.
-
타겟 클러스터 트레이닝: 비슷한 주식 군집의 데이터를 활용하여 맞춤형 모델링을 수행합니다.
-
대상 변환: 미래 수익을 더 잘 예측하기 위해 대상 변수를 수정합니다.
-
GLM 활용: 일반화 선형 모델(GLM) 기법을 사용하여 연속적인 수익 예측에는 선형 회귀를, 범주형 예측에는 로지스틱 회귀를 적용합니다.
-
선택적 특징 통합: 예측 성능을 향상시키기 위해 특징 선택 전략을 사용합니다.
모델 형식은 다음과 같습니다:
아래는 Markdown 형식으로 표현한 내용입니다.
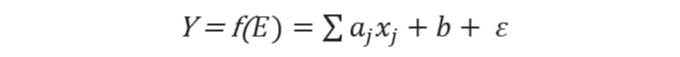
주식 수익률(E)의 링크 함수:
- 모델 1: Y = f(E) = E: 선형 회귀
- 모델 2: Y = f(E) = (E`t) + 0: 이진 분류
예측 기간 및 특성 생성:
가장 최근 시점부터 10번째까지의 수익률을 예측하기 위해 다음과 같이 계산합니다:
train_df['return'] = 100 * (train_df['smooth_price_1'] - train_df['smooth_price_10']) / train_df['smooth_price_10']
포함된 특성은 다음과 같습니다:
수익률의 변동성: 연속된 부드러운 가격 간 백분율 변동의 표준편차입니다.
과거 수익률 특징: "smooth_price11"과 이후 가격 간 수익률 구간을 위한 9개의 새 열(past_return_1에서 past_return_9)입니다.
이차 상호 작용 항목: 특성 선택 이후 선택된 것입니다.
파이썬으로 구현된 특성 엔지니어링:
for i in range(24, 0, -1):
train_df[f'return_{i}'] = (train_df[f'smooth_price_{i}'] - train_df[f'smooth_price_{i+1}']) / train_df[f'smooth_price_{i+1}']
train_df['risk_return'] = train_df[return_columns[0:15]].std(axis=1)
train_df['risk_return_2'] = train_df['risk_return']**2
Generalized Linear Models (GLM)을 사용한 모델링:
특성 선택 후에, 중요한 특성들인 risk_return, 과거_return_2의 이차항, 그리고 이 둘의 상호작용을 사용하여 주식 수익률 예측을 위해 GLM을 적용합니다.
import statsmodels.api as sm
X = sm.add_constant(train_df_clus0[['risk_return', 'past_return_2_squared', 'risk_past_interaction']])
y = np.log(train_df_clus0['return'] + 1) # 안정성을 위한 로그 변환
model = sm.OLS(y, X).fit()
print(model.summary())
이 모델은 이 예제에서 다루지 않은 특징 선택 과정을 거친 후 선택된 특징을 사용합니다:
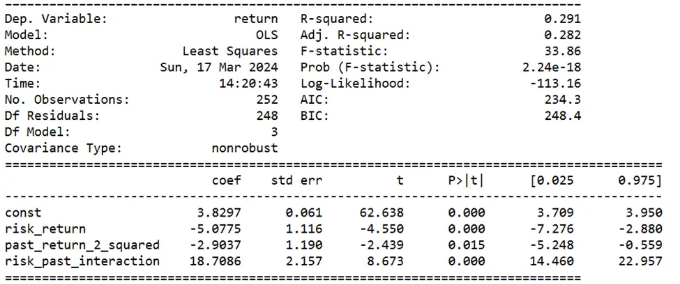
모델의 수정된 R-제곱은 약 29%로, 주식 시장에서 정확한 수익률 예측에는 제한이 있음을 나타냅니다. 그러나 주식 선택에 대한 유용성은 주목할만 합니다. 중요한 예측 변수에는 risk_return, past_return_2의 이차항 및 risk_return과 past_return_2의 상호 작용 항이 포함되어 있으며, 이들이 분석에서의 관련성을 보여줍니다.
이진 분류를 위한 로지스틱 회귀:
특정 수익 임계값을 넘을지 예측하는 데 적합한 경우, 로지스틱 회귀 모델을 구축하였습니다:
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import roc_auc_score, roc_curve
logist_model = LogisticRegression().fit(X_train, y_train)
pred_probs = logist_model.predict_proba(X_test)[:, 1]
auc = roc_auc_score(y_test, pred_probs)
print(f'AUC: {auc}, KS 통계량: {ks}')
AUC가 82%이고 KS 통계량이 61%인 경우, 로지스틱 모델은 테스트 데이터에서 주식 선택을 검증하는 데 강력한 성능을 보여줍니다. 이러한 메트릭은 해당 수익 임계값을 초과할 것으로 예상되는 주식을 구분하는 모델의 능력을 강조합니다.
SHAP 값을 사용하여 주식 성과를 분석합니다.
SHAP 값은 개별 주식 영향을 깊이 이해하게 도와주며, 정확한 전략 개발을 가능케 합니다. 'std'와 같은 특정 원인을 강조함으로써, SHAP 값은 변동성이 수익 잠재력에 미치는 영향을 나타내며, 전반적인 특성 분석을 보완하면서 모델 정확도를 직접적으로 평가하지 않아도 됩니다.
먼저 shap_values를 사용하여 모델의 모든 핵심 원인에 대한 전역 영향을 보여주는 막대 그래프를 생성합니다:
model = sm.OLS(y, X[cols]).fit()
# 모델의 p-값을 얻기 위해 모델 요약을 출력합니다
explainer = shap.Explainer(model.predict, X[cols])
# SHAP 값을 계산합니다
shap_values = explainer(X[cols])
shap.plots.bar(shap_values)
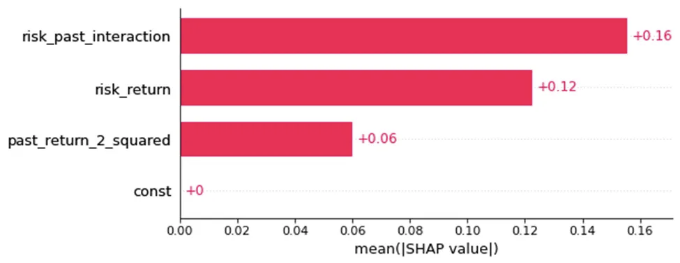
과거 위험_수익 및 과거 수익과 상호 작용 항목이 중요하게 나타나는 것을 보여주며, 막대 플롯은 전체 효과를 시각화합니다.
자세한 영향 분포를 보려면 bee swarm plot을 사용할 수 있습니다:
shap.plots.beeswarm(shap_values)
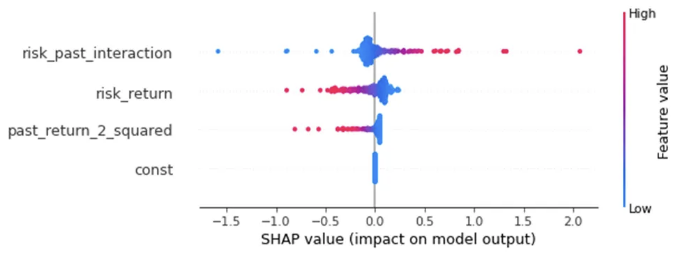
상호 작용 변수 risk_past_interaction에는 값에 따라 다양한 기여도가 있음을 보여줍니다.
'ORCL'과 같은 개별 주식에 중요한 주요 요인의 영향을 조사하려면 로컬 막대 플롯이 유용합니다:
ORCL_index = X[X['ticker'] == 'ORCL'].index
ORCL_shap_values = shap_values[ORCL_index[0]]
shap.plots.bar(ORCL_shap_values)
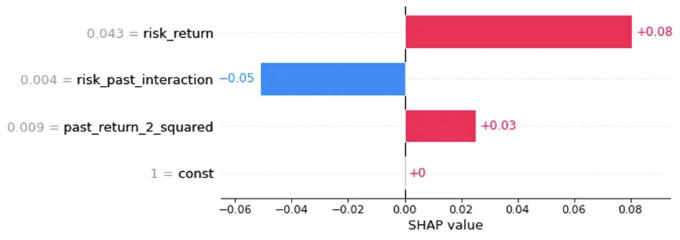
클러스터 내 각 주식에 대한 주요 영향을 미치는 기능을 수집하는 것은 효과적인 거래 전략을 만드는 데 중요합니다. 아래는 이러한 주요 요인을 정확하게 파악하고 정리하기 위해 설계된 Python 코드입니다:
import pandas as pd
import numpy as np
# 'tickers'를 'X'의 관측치와 맞춘다고 가정
tickers = train_df_clus0['ticker'].values
# 데이터를 수집하기 위한 딕셔너리 준비
data = {
'ticker': [],
'top_feature1': [], 'top_feature2': [], 'top_feature3': [],
'importance1': [], 'importance2': [], 'importance3': []}
# 각 주식에 대해 상위 3개의 주요 영향 요소를 추출하기 위해 SHAP 값 순서대로 반복
for i, ticker in enumerate(tickers):
sorted_indices = np.argsort(-np.abs(shap_values.values[i]))[:3]
data['ticker'].append(ticker)
data['top_feature1'].append(cols[sorted_indices[0]])
data['top_feature2'].append(cols[sorted_indices[1]])
data['top_feature3'].append(cols[sorted_indices[2]])
data['importance1'].append(shap_values.values[i][sorted_indices[0]])
data['importance2'].append(shap_values.values[i][sorted_indices[1]])
data['importance3'].append(shap_values.values[i][sorted_indices[2]])
# 수집한 데이터를 쉽게 분석하기 위해 DataFrame으로 변환
df_key_drivers = pd.DataFrame(data)
여기에는 각 주식의 상위 2개 기능 및 그 중요성을 보유한 결과 데이터 프레임이 있으며, 목표 주식 선택을 돕습니다.
주식 선정 최적화를 위한 응답 표면 방법론 (RSM)
이 프로젝트는 RSM을 사용하여 주식 선택을 최적화하며, 과거 변동성과 성과 사이의 이차 관계를 활용하여 미래 수익을 예측합니다. 우리는 리스크_리턴(수익률 변동성)과 과거 수익을 포함하는 회귀 모델을 사용하여 재무 데이터의 비선형 경향과 변동성을 고려합니다.
우리는 RSM을 적용하여 두 가지 주요 목표를 가지고 있습니다:
- 과거 가격, 변동성 및 미래 수익 사이의 관계 모델링.
- 예측된 미래 수익을 극대화하는 최적 조건을 찾기.
다음은 응답 표면을 시각화하는 Python 코드입니다:
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# 모델 적합 및 응답 표면 데이터 생성
X = sm.add_constant(train_df_clus0[['risk_return', 'past_return_2_squared', 'risk_past_interaction']])
model = sm.OLS(y, X).fit()
x_range = np.linspace(DF['past_return'].min(), DF['past_return'].max(), 100)
y_range = np.linspace(DF['risk_return'].min(), DF['risk_return'].max(), 100)
x_grid, y_grid = np.meshgrid(x_range, y_range)
z_grid = model.params[0] + \
model.params[1]*y_grid + model.params[2]*x_grid**2 + \
model.params[3]*x_grid*y_grid
# 응답 표면 플로팅
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(x_grid, y_grid, z_grid, cmap='viridis')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
plt.show()
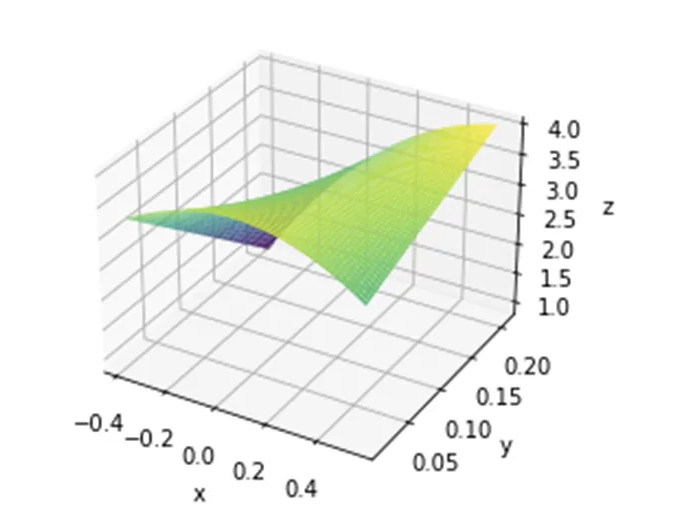
표면의 곡선은 이차 관계를 통합하는 모델의 용량을 확인합니다.
최고 주식을 정확하게 찾기 위해 각 주식의 위치를 이상적인 지점과 비교하여, 거리 측정 기준에 따라 가장 가까운 다섯 개를 선택합니다:
# 최적 지점까지의 거리 계산
DF['distance'] = np.sqrt((DF['past_return'] - optimal_x)**2 + (DF['risk_return'] - optimal_y)**2)
# 'distance' 열을 기준으로 DataFrame 정렬
DF_sorted = DF.sort_values('distance')
# 최적 지점에 가장 가까운 상위 10개의 주식 선택
top_10_stocks = DF_sorted.head(10)
print("최적 지점에 가장 가까운 상위 10개 주식:")
print(top_10_stocks[['ticker', 'past_return', 'risk_return', 'distance']])
여기에 선택된 상위 10개 주식이 있습니다:
아래는 Markdown 형식으로 변경한 표입니다.
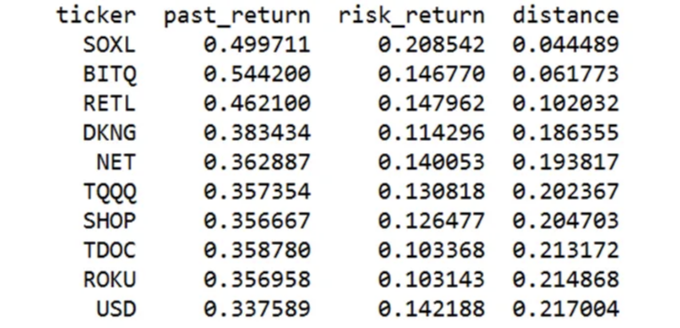
우리는 최적 지점에 독점적으로 의존하지는 않지만, 그것은 이상적인 주식 조건에 대한 기준을 제공합니다. 이를 찾기 위해:
# 미래 수익을 극대화하기 위한 최적 지점 찾기
optimal_idx = np.argmax(z_grid)
optimal_x = x_range[optimal_idx // 100]
optimal_y = y_range[optimal_idx % 100]
optimal_z = z_grid.flatten()[optimal_idx]
print(f"최적 지점: 과거 수익 = {optimal_x}, 위험 수익 = {optimal_y}, 미래 수익 = {optimal_z}")
최적 지점: 과거 수익 = 0.544199942617375, 위험 수익 = 0.2085424594952841, 미래 수익 = 4.13061405635688
RSM을 활용하여 유망한 주식 선정을 신호하는 시장 조건을 전략적으로 식별할 수 있습니다.
결론
이 분석에서는 주식 가격 예측과 투자 전략 수립을 향상시키기 위해 데이터 과학 기술과 금융 통찰력을 결합했습니다. 추세 식별을 위한 데이터 평활화, 주식 분류를 통한 집중 조사, 예측 모델의 배치를 통해 주식 시장 흐름의 복잡성을 탐색했습니다.
이 연구는 특정 시간대의 데이터를 기반으로 하고 있다는 점을 인지하는 것이 중요합니다. 시장 흐름(bull/bear phase), 이자율, 세계 경제 풍향, 산업 특정 트렌드를 포함한 다양한 변수에 민감한 금융 시장을 고려할 때, 우리 모델의 적용 가능성은 서로 다른 기간에 따라 다를 수 있습니다.
이러한 한계에도 불구하고, 본 연구는 페어 트레이딩이나 예측 응답을 기반으로 한 선택적 주식 투자와 같은 실행 가능한 전략을 제시하여 전략적 사고를 강화하고자 합니다. 이러한 데이터 과학과 전통적인 금융 분석의 결합은 빠르고 예측할 수 없는 변화에 취약한 시장에서 투자자가 결정을 내리는 데 도움이 되는 도구를 제공하기 위한 것입니다.