선형 회귀는 머신 러닝 세계에서 가장 기본적인 알고리즘 중 하나이며, 분석의 ABC와 같습니다.

하늘의 별무리를 통해 가장 적합한 선을 만든다고 생각해보세요. 여기서 각 별은 데이터 점을 나타냅니다.

오늘은 선형 의존성의 클래식 예시 중 하나인 키와 몸무게를 활용해 실제 세계 머신 러닝에 대해 알아보겠습니다 👇🏻

기본 원리 이해하기

간단한 선형 회귀는 가장 기본적인 머신러닝 알고리즘입니다. 데이터 모델링에 대한 여정을 시작하는 대부분의 경우입니다.

신장과 몸무게를 그래프로 그려보면, 신장이 증가함에 따라 몸무게도 증가하는 선이 대략적으로 나타날 것입니다.

그것이 선형 회귀의 핵심입니다.

그러니까 이 작업을 어떻게 수행할 수 있는지 살펴보겠습니다...

#1. 데이터 탐색 - 뛰기 전에 훔쳐보기

분석에 들어가기 전에 데이터와 친해지는 것부터 시작해봐요.

세 개의 열이 있는 테이블을 상상해보세요: 성별, 키, 몸무게.

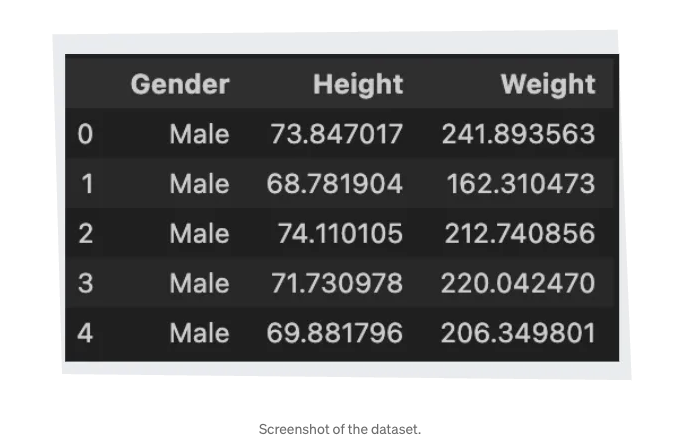
파이썬의 df.info()로 간단히 살펴보면 수천 개의 항목이 있고 중요한 것은 결측값이 없다는 것입니다.

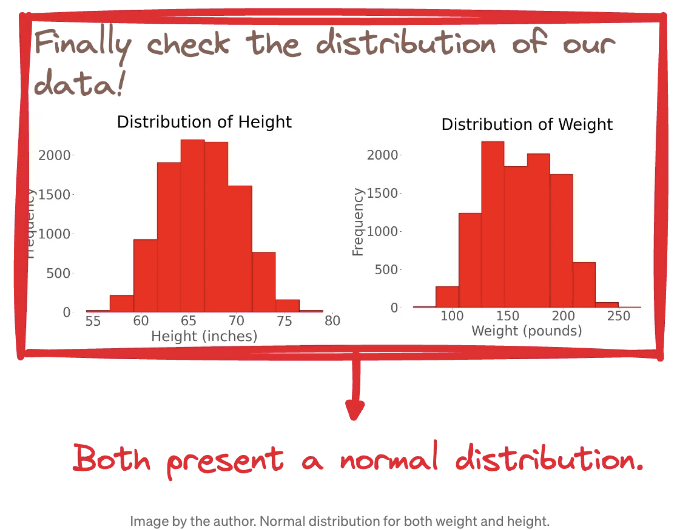
그리고 데이터의 분포는 어떤가요?

키에 대한 종모양 곡선 하나와 몸무게에 대한 종모양 곡선 하나를 생각해보세요. 두 곡선 모두 나비 날개만큼 대칭적인데요 — 바로 여기가 우리의 정규 분포입니다.

#2. 최적 선을 찾는 방법

우리의 최적 선을 얻기 위해서는 여러 가지 방법이 있습니다. 오늘날 대다수의 사람들은 scikit-learn을 활용하여 미리 빌드된 선형 회귀 알고리즘을 적용할 것입니다.

그러나 이번에는 최초로 세 가지 다른 방법을 시도해 봅시다:

• 2 DIY — 모두 스스로 알고리즘 생성.
• 1 최종 방법은 scikit-learn 활용하는 것.

접근 방법 #1: 최소 제곱법 (OLS)

최소 제곱법(OLS)의 목적은 예측 오차의 제곱을 최소화하여 최적의 계수 A와 B를 결정하는 것입니다 — 이것이 바로 선형 회귀의 비용 함수인 MSE입니다.

미적분을 활용하여 비용 함수의 최소값을 찾기 위해 편미분의 성질을 이용합니다. 그리고 이러한 편미분이 0이 되는 지점이 최소값에 해당합니다.

위 수학 문제를 해결하여 A와 B에 대한 정확한 닫힌 수학 공식을 얻게 되면, 가장 정확한 선형 모델로 향하는 직접적인 경로를 얻을 수 있습니다.

이것은 이러한 수학적인 닫힌 해결책을 찾기 위해 몇 줄의 코드를 정의하는 것으로 번역됩니다. 그래서 매우 직관적입니다.

방법 #2: 경사하강법 — 산에서의 하이킹

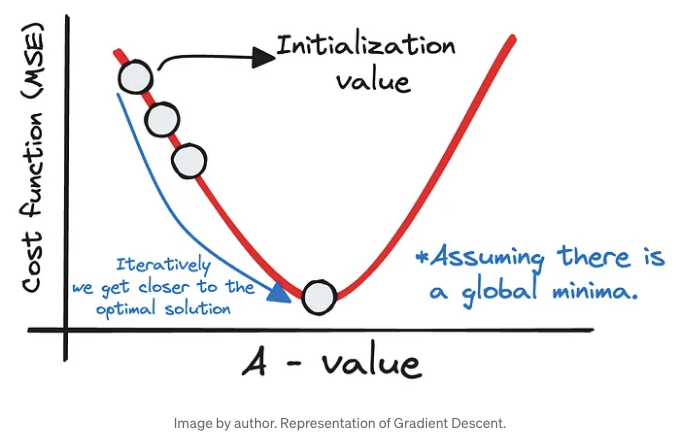
경사 하강은 비용 함수를 최소화하는 데 사용되는 중요한 최적화 알고리즘으로, 예측 모델의 가장 정확한 가중치 값을 찾는 데 도움을 줍니다.

언덕 꼭대기에 서 있는 것으로 상상해보세요. 여러분의 목표는 아래의 계곡에 있습니다. 이것은 비용 함수의 최솟값을 나타냅니다.

이를 달성하기 위해 가중치 A와 B에 대한 초기 추정치로 시작하여 이 추정치를 반복적으로 개선합니다.

이 과정은 언덕을 내려가는 것과 유사합니다. 각각의 단계에서 우리는 주변 환경을 평가하고, 각각의 다음 단계가 계곡 바닥에 더 가까워지도록 우리의 궤적을 조정합니다.

이러한 단계는 학습 속도에 의해 안내됩니다 — 방정식에서 lr로 상징되는 중요한 하이퍼파라미터입니다. 이 학습 속도는 매개변수 A와 B에 대한 조정이나 단계의 크기를 제어하여 최소값을 초과하지 않도록 합니다.

각 단계에서 비용 함수의 A 및 B에 대한 편도함수인 dA와 dB를 계산합니다. 이 도함수는 우리에게 비용 함수가 가장 빨리 감소하는 방향을 가리키는데, 이것은 비유적인 언덕에서 가장 가파른 하강 경로를 찾는 것과 유사합니다.

각 반복에서 A와 B에 대한 업데이트된 방정식은 다음과 같습니다.

지침대로 테이블 태그를 마크다운 형식으로 변경하겠습니다.

This meticulous process is repeated until we reach a point where the cost function’s decrease is negligible, suggesting we’ve arrived at or near the global minimum — our destination where the predictive error is minimized, and our model’s accuracy is maximized.

This translates into defining two main functions:

• The function to compute MSE

• A 및 B를 업데이트하는 기능

우리는 코드를 다음과 같이 초기화합니다:

• A = 0
• B = 0
• 학습률 0.0001(학습률은 알고리즘이 더 빠르게 또는 더 느리게 학습할 수 있도록 합니다).
• 최대 반복 횟수

그래서 최종 코드는 다음과 같습니다:

접근 방법 #3: Sci-Kit Learn — 파이썬의 강력한 무브

파이썬을 좋아하는 사람들을 위해, Sci-Kit Learn은 머신 러닝을 위한 스위스 아미 나이프입니다. 회귀, 분류, 클러스터링 등을 위한 다양한 도구로 가득합니다.

우리가 해야 할 일은 LinearRegression 라이브러리를 가져와서 객체를 만들고, 데이터로 훈련시키는 것뿐입니다.

몇 줄의 코드로 이를 구현할 수 있습니다:

왔어요!

우리의 모델이 준비되었습니다.

3. 최종 결과

우리의 기술을 적용한 후, 공식이 생성되었습니다:

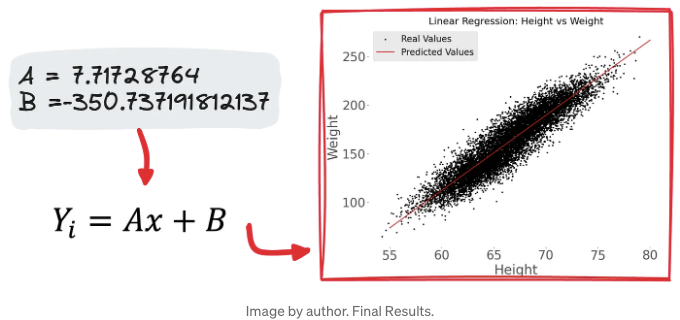
With the data we crunched, A turned out to be around 7.17, and B was approximately -350.73.

What does this mean?

For every inch of height, the weight increases by about 7.17 units, minus our intercept value.

가정 게임

어떤 모델도 완벽하지 않으며, 선형 회귀는 특정 가정에 의존합니다:

• 선형성: 우리의 데이터는 선이 되어야 합니다. 기억해주세요. 이미 간단한 산점도로 이 선형 패턴을 첫 번째 분석에서 확인했습니다.
• 독립성: 입력 변수는 서로 독립적이어야 합니다.
• 잔차의 정규 분포: 관측값과 예측값의 차이는 종 모양의 곡선을 형성해야 합니다.

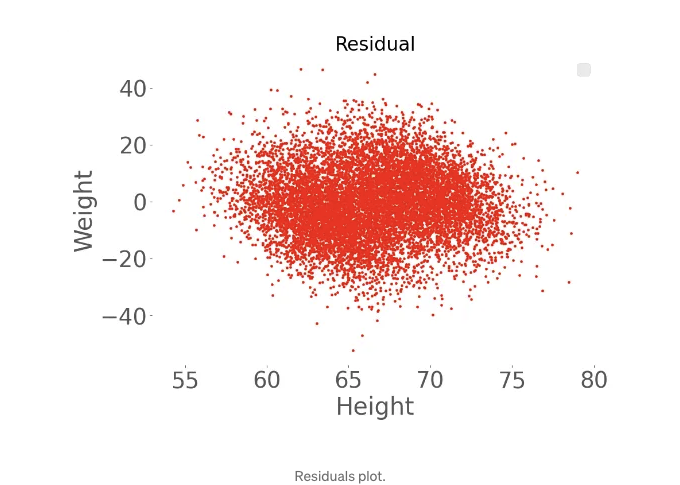
• 잔차의 등분산성: 오차의 퍼짐은 독립 변수의 모든 값에서 일관되어야 합니다.

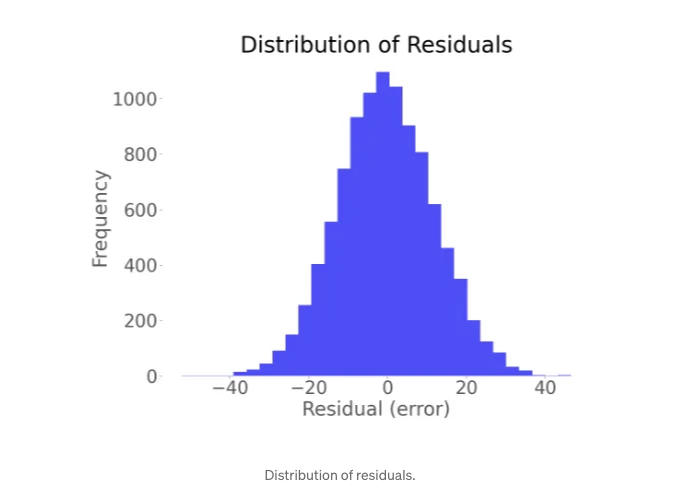
마무리의 생각

선형 회귀는 간단한 것처럼 보일 수 있지만, 데이터 과학 무기함에 속한 강력한 도구입니다.

데이터 분석의 매력은 그 간단함에 있습니다.

복잡한 모델을 사용하는 것이 중요한 게 아니라, 올바른 모델을 올바른 상황에 사용하는 것이 중요한 거죠.

이 개념을 소화하면, 당신은 데이터 속에 숨겨진 이야기를 발견하는 길에 여러분이 잘 나아가고 있습니다.

호기심을 가져라, 데이터 우주를 계속 탐험해 보세요! 🤓

다음의 GitHub 저장소에서 코드를 확인할 수 있어요.

ForCode’Sake를 팔로우하면 이와 유사한 기사를 더 많이 볼 수 있어요! ✨

MLBasics 이슈가 마음에 드셨나요? 그렇다면 DataBites 뉴스레터에 가입하여 최신 내용을 이메일로 받아보세요!

유니크한 콘텐츠를 약속합니다!

아래 Markdown 형식의 표를 확인하세요.

데이터 과학자 또는 데이터 엔지니어가 되기 위한 훌륭한 데이터 과학 로드맵을 확인해보세요! 🤓

또한 ML, SQL, Python 및 DataViz에 관한 매일 게시하는 치트 시트를 확인할 수 있는 X, Threads 및 LinkedIn에서 저를 만날 수도 있습니다.