
최단 경로 찾기는 컴퓨터 과학에서 기본적인 문제로, 네트워크 라우팅 프로토콜부터 그래프 분석까지 다양한 알고리즘과 응용프로그램의 기초를 형성합니다. 현실에서는 물류 및 통신 네트워크에서 효율적인 경로를 찾고 여행 시간을 최소화하는 데 핵심적인 문제입니다.
이 문제가 이렇게 중요하기 때문에 많은 사람들이 이를 해결하는 방법에 대해 고민했습니다. 이는 다양한 가정과 실행 시간을 가진 다양한 알고리즘의 동물원으로 이어졌습니다. 이 글에서는 벨만-포드 알고리즘의 작동 방식과 Python 및 Rust에서의 구현 방법을 보여 드리고자 합니다.
(Shimbel-)벨만-포드(-무어) 알고리즘
알고리즘의 이름부터 헷갈릴 수 있어요. 문헌에서는 벨만-포드 알고리즘으로 알려져 있지만 많은 사람들이 관여했습니다. Alexander Schrijver의 논문 "조합 최적화의 역사에 대하여"에 따르면, Alfonso Shimbel은 1955년에 동등한 알고리즘을 개발했고, Richard Bellman과 Lester Ford Jr.은 각각 1958년과 1956년에 이 알고리즘을 설명했습니다. 이후 Edward F. Moore가 1959년에 알고리즘의 변형을 발표했어요. 하지만 걱정하지 마세요, 이 알고리즘 자체는 그 역사보다 이해하기 쉬워요.
이들의 알고리즘은 여러분이 주어진 그래프의 고정된 노드에서 시작하여 다른 각 노드까지의 최단 경로 문제를 해결해요. 다음과 같은 그래프를 예시로 삼아볼게요:
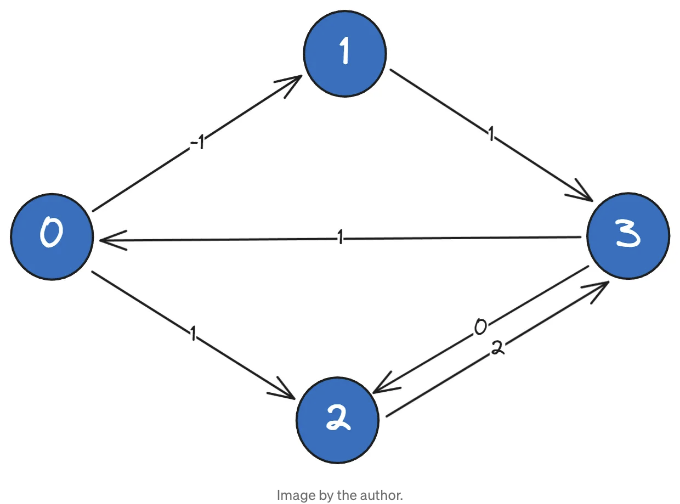
총 6개의 방향성이 있는 에지로 연결된 네 개의 노드를 볼 수 있어요. 각 에지는 가중치가 있습니다. 예를 들어, 3에서 0으로 가는 에지의 가중치는 1이에요. 노드 0에서 노드 2로의 최단 경로는 직접적인 0-2가 아닌 총 비용이 (-1)+1+0 = 0인 0-1-3-2일 수 있어요. 이제 이러한 경로를 알고리즘적으로 찾는 고수준 아이디어에 대해 이야기해볼게요.
아이디어
알고리즘은 시작 노드로부터 i개 이하의 엣지를 사용하여 다른 모든 노드까지의 최단 경로의 길이를 배열 형태로 유지하는 간단한 아이디어를 중심으로 돌아갑니다.
이 배열을 i = 0, 1, ...부터 순차적으로 계산합니다. 각 반복에서 i에 대한 정보는 이전 반복 i-1의 배열과 그래프의 엣지를 사용합니다.
예시
자 그럼 이제 작은 예제를 사용해보자. 노드 0에서 다른 모든 노드로 가는 최단 경로 길이를 찾고 싶다고 가정해보자. 나중 단계에서 실제 경로도 재구성할 것이지만, 일단은 일 노드 간의 경로 길이에만 관심을 갖자.
거리 배열을 [0, ∞, ∞, ∞]로 시작한다. 즉, 우리는 최대 edge 0을 사용하여 0 노드에서 0 노드로 총 길이 0만큼 도달할 수 있다는 것이다. 이것은 우리가 정한 정의다. 두 번째 항목은 0 노드에서 1 노드로 최대 edge 0을 사용하여 ∞ 길이로 도달할 수 있음을 의미하는데, 즉 해당 노드에 도달할 수 없다는 것이다. 동일한 이유로 0 노드에서 2와 3으로 가는 것도 동일하다.
거리를 해당 노드 옆에 써보자:
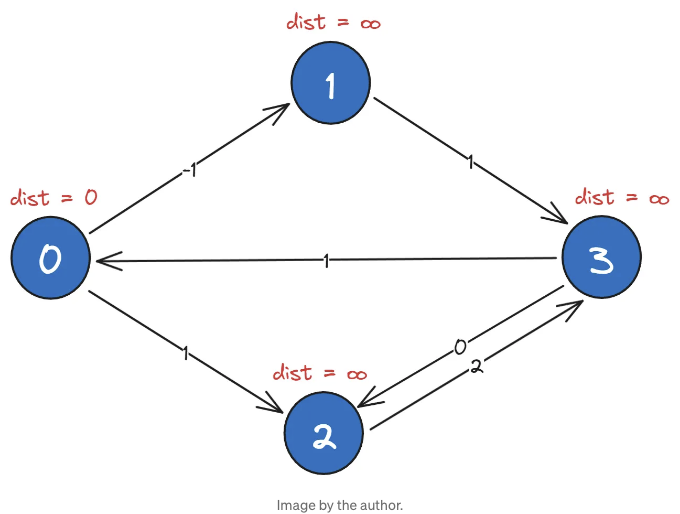
다음 반복에서는 최소경로 길이를 포함하는 다른 배열 [a, b, c, d]를 채우려고 합니다. 이 배열은 노드 0에서 최대 한 개의 엣지를 사용하여 다른 모든 노드까지의 최단 경로 길이를 포함합니다. 이전 배열을 사용하여 이를 어떻게 계산하는지 살펴봅시다. 예를 들어, 노드 0에서 1까지의 최단 경로 길이를 알고 싶다면 두 가지 가능성이 있습니다:
-
0에서 1까지 엣지를 사용하지 않고 이동하거나
-
0에서 1까지 추가 엣지를 사용하여 이동합니다.
옵션 1은 이전 배열 [0, ∞, ∞, ∞]에서 볼 수 있듯이 길이가 ∞입니다. 두 번째 옵션의 길이는 -1이며 그래프를 통해 노드 0에서 노드 1로 -1의 비용으로 이동할 수 있습니다. 분명히 이전에 보았던 ∞보다 -1이 더 작으므로 배열에 이를 넣어 보겠습니다. 다른 노드에 대해 동일한 작업을 수행하면 업데이트된 배열 [0, -1, 1, ∞]이 됩니다. 이제 이 반복이 완료되었습니다.
그래픽적으로表시하면:
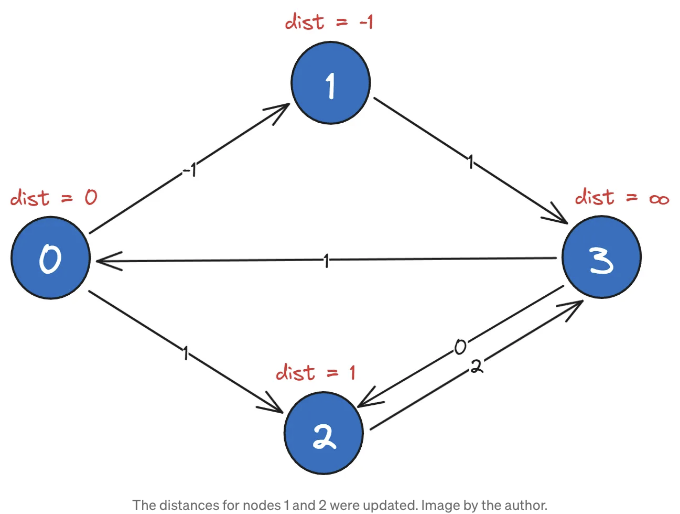
다음 이터레이션에서는 같은 게임을 다시 합니다. 노드 0에서 다른 모든 노드로 가는 최단 경로 길이가 최대 두 개의 변을 사용하여 [a, b, c, d]를 채우고 싶습니다. 예를 들어, 노드 0에서 노드 3까지의 최단 경로 길이를 계산해 봅시다. 노드 0에서 노드 3으로 가는 여러 옵션이 있습니다:
- 단일 변을 사용하여 0에서 3으로 이동: 길이는 이전 이터레이션의 배열에서 볼 수있는대로 ∞입니다.
- 먼저 노드 1로 이동한 다음 1에서 3으로 가는 변을 사용할 수 있습니다. 하나의 변만 사용하여 노드 1로 가는 데 드는 비용은 배열에서 확인할 수 있는대로 -1입니다. 노드 1에서 노드 3으로 한 단계 더 가는 데 드는 비용은 그래프에서 확인할 수 있는대로 1입니다. 따라서 이미 이전 옵션보다 작은 비용인 0으로 노드 0에서 노드 3에 도달할 수 있습니다.
- 먼저 노드 2로 이동한 다음 2에서 3으로 가는 변을 사용할 수 있습니다. 따라서 노드 0에서 노드 3으로 2 단계로 도달하여 비용은 1 + 2 = 3입니다.
다른 옵션이 없으므로 두 번째 옵션에서 최단 경로 길이는 0입니다. 다른 노드에 대해도 수행하면 배열 [0, -1, 1, 0]을 얻을 수 있습니다.
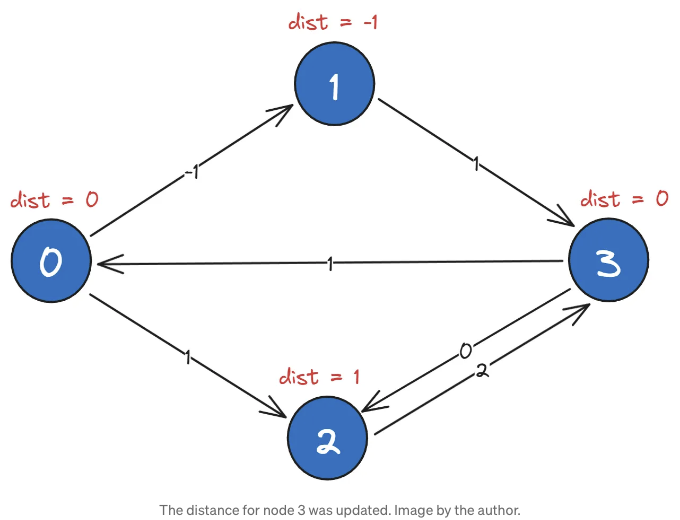
이전 배열 [0, -1, 1, 0]에서 시작하는 한 번 더의 반복 작업을 합니다. 이번 반복에서는 노드 0에서 노드 2로의 최단 경로 길이가 변하는 것 외에는 큰 변화가 없습니다. 이전 배열에서 볼 수 있듯이, 최대 두 개의 엣지를 사용하여 길이가 1인 것을 알 수 있습니다. 그러나 처음에 우리는 실제로 길이가 (-1) + 1 + 0 = 0인 0–1–3–2의 최단 경로를 보았습니다. 우리는 현재 반복에서 이 경로 길이를 찾을 것이며, 그러면 알고리즘이 종료됩니다. 이것은 네 개의 노드를 가지면 최단 경로가 최대 세 개의 엣지만을 포함해야 하거나 일반적으로 N 노드를 가지면 N— 1개의 엣지를 포함해야 하기 때문입니다.
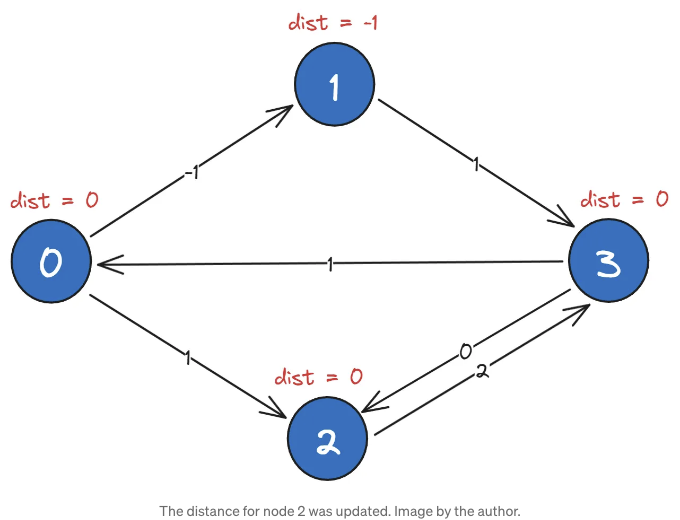
음수 순환이란
마지막 문장에서 조금 거짓말을 한 것 같아요. 음의 순환이 존재할 수 있다는 건데요, 예를 들어 노드 u에서 자신으로 돌아와 경로의 총 길이가 0보다 작은 것입니다. 이 경우 순환을 돌 때마다 경로의 길이를 줄일 수 있기 때문에 최단한 경로가 없는 것이죠. 음의 순환을 찾으려면 N개의 노드가 있을 때 N번째 반복을 실행해야 합니다. 음의 순환하지 않는다면 이 반복에서 우리 배열이 변하지 않아야 합니다. 이것이 여전히 변경된다면, 어딘가에 음의 순환이 있다는 것을 알 수 있습니다. 이를 복원할 수도 있지만, 여기서는 그렇게 하지 않겠습니다.
구현
작은 코드량에 대한 많은 글입니다. 두 가지 다른 프로그래밍 언어인 Python과 Rust로 어떻게 하는지 살펴봅시다.
Python
여기 있습니다. 제가 경로 길이 뿐만 아니라 가장 짧은 경로를 재구성할 수 있는 다른 배열 prev도 계산합니다.
N = 4
graph = {0: {1: -1, 2: 1}, 1: {3: 1}, 2: {3: 2}, 3: {0: 1, 2: 0}}
start = 0
dists = [float("inf") for i in range(N)]
prev = [None for i in range(N)]
dists[start] = 0
prev[start] = start
for _i in range(N):
for node, edges in graph.items(): # 모두에 대해 반복
for next_node, weight in edges.items(): # `node`에서 시작하는 모든 간선에 대해 반복
candidate_length = dists[node] + weight
if candidate_length < dists[next_node]:
dists[next_node] = candidate_length
prev[next_node] = node # `node`에서 `next_node`로 이동하는 것이 이전 경로보다 나은 것
for node, edges in graph.items():
for next_node, weight in edges.items():
if dists[node] + weight < dists[next_node]:
print("음의 사이클이 감지되었습니다!")
print(dists)
print(prev)
출력은 다음과 같습니다.
[0, -1, 0, 0]
[0, 0, 3, 1]
첫 번째 배열은 노드 0부터 노드 0, 1, 2 및 3으로 가는 가장 짧은 경로가 각각 0, -1, 0 및 0임을 나타냅니다.
노드 0에서 노드 2로 길이가 0인 경로를 어떻게 얻을 수 있을까요? 두 번째 배열 prev를 살펴봅시다. 거기서 prev[2] == 3 이므로 노드 3에서 노드 2로 이동합니다. 따라서 경로는 3–2로 끝납니다. 또한 노드 3에서 노드 1로 이동한다는 것을 알 수 있습니다. 따라서 경로는 1–3–2로 끝납니다. 그리고 노드 1에서 노드 0으로 이동한다는 것을 알 수 있습니다. 따라서 전체 경로는 0–1–3–2 입니다.
좋아요, Rust에서 같은 작업을 해봅시다!
Rust
한 줄 씩 번역해 보았습니다. Rust에 관심이 있는 분들에게 도움이 될 수도 있을 것 같아요.
use std::collections::HashMap;
fn main() {
const N: usize = 4;
let graph: HashMap<usize, HashMap<usize, f32>> = HashMap::from([
(0, HashMap::from([(1, -1.), (2, 1.)])),
(1, HashMap::from([(3, 1.)])),
(2, HashMap::from([(3, 2.)])),
(3, HashMap::from([(0, 1.), (2, 0.)])),
]);
let start: usize = 0;
let mut dists = [f32::INFINITY; N];
let mut prev = [None::<usize>; N];
dists[start] = 0.0;
prev[start] = Some(start);
for _i in 0..N - 1 {
for (node, edges) in graph.iter() {
for (next_node, weight) in edges.iter() {
let candidate_length = dists[*node] + *weight;
if candidate_length < dists[*next_node] {
dists[*next_node] = candidate_length;
prev[*next_node] = Some(*node);
}
}
}
}
for (node, edges) in graph.iter() {
for (next_node, weight) in edges.iter() {
if dists[*node] + *weight < dists[*next_node] {
println!("Negative cycle detected!");
}
}
}
println!("{:?}", dists);
println!("{:?}", prev);
}
실행 시간과 메모리
이 알고리즘은 그래프의 노드 수를 의미하는 N과 그래프의 간선 수를 의미하는 E에 대해 O(N · E) 시간에 실행된다는 것을 확인할 수 있어요. 이는 모든 N 노드를 순회하는 루프와 모든 E 간선을 순회하는 내부 루프가 중첩되어 있기 때문에 나타나는 직접적인 결과입니다.
메모리 사용량 측면에서는 추가로 크기가 N인 두 개의 배열과 몇 개의 상수만 저장하면 되므로 추가 메모리 복잡도는 O(N)이 됩니다.
프로그래밍 언어의 성능 측정가들을 위해: 내 Python 버전은 평균적으로 노드당 10개의 이웃을 갖는 랜덤 1000개 노드 그래프에서 3초가 걸렸지만, Rust 버전은 동일한 그래프에서 0.5초가 걸렸습니다.
결론
이 글에서는 한 노드로부터 모든 노드까지의 최단 경로 길이와 최단 경로를 찾는 방법을 배웠습니다. 이를 위해 우리는 벨만-포드 알고리즘을 선택했습니다. 이 알고리즘은 빠르고 간단하며 효율적으로 구현할 수 있으며 추가 메모리를 많이 사용하지 않는 편리한 알고리즘입니다.
더 빠른 알고리즘인 다익스트라 알고리즘을 사용할 수는 없지만, 우리 예시에는 사용할 수 없습니다. 다익스트라 알고리즘은 양의 간선 가중치를 전제로 하기 때문이죠. 그래서 약간의 음의 간선 가중치를 더해 다른 알고리즘을 사용해야 했어요. 😉
그래서 최단 경로 알고리즘을 구현하거나 이를 대신 처리해주는 라이브러리를 사용해야 할 때, 그 알고리즘이 어떻게 작동하는지 이해하게 되었으면 합니다.
오늘 새롭고 흥미로운 가치있는 것을 배우셨기를 바랍니다. 읽어주셔서 감사합니다!