자동 모델 선택 및 다단계 예측

ARIMA (AutoRegressive Integrated Moving Average)은 시계열 예측 및 분석에 사용되는 통계 모델입니다. ARIMA의 기원은 1900년대 초반으로 거슬러 올라가며 자기회귀(AR) 모델과 이동평균 (MA) 모델이 별도로 발전됐습니다. 두 모델 모두 현실 시계열 데이터의 복잡한 역학을 포착하기에는 충분하지 않은 것으로 나타납니다. 1960년대에 세 통계학자인 조지 E. P. 박스, 그윌림 M. 젠킨스, 그리고 그레고리 C. 레인절이 "시계열 분석: 예측과 제어"라는 책에서 AR과 MA 모델을 공식적으로 통합하여 ARIMA를 만들었습니다.
ARIMA는 아마도 가장 잘 알려진 패러다임이지만, 왜 이 "현대적인" 시계열 서적에 포함시키는 걸까요? 주된 이유는 AR과 MA가 현대적인 시계열 기술에서 많은 흔적을 남겨주었기 때문입니다. ARIMA에 대한 기본 이해는 다른 복잡한 모델에 걸쳐 활용할 수 있게 해줍니다. 예를 들어, NeuralProphet의 4장에서 AR 모듈을 보았고, 12장과 13장에서는 AR 항목을 감독 학습 모델에서 특징으로 볼 것입니다. 이 책에 ARIMA를 포함한 두 번째 이유는 최근의 코드 개발로 자동 모델 선택과 다단계 예측이 가능해졌기 때문입니다.
- 챕터 4: "튜토리얼 II: 트렌드 + 계절성 + 휴일 및 이벤트 + 자기 회귀(AR) + 지연 회귀자 + 미래 회귀자."
- 챕터 12: "트리 기반 시계열 예측에 대한 튜토리얼"
- 챕터 13: "다단계 시계열 예측에 대한 튜토리얼."
오늘날의 코드 라이브러리를 사용하면 최적의 ARIMA 모델을 선택할 수 있습니다. 표준 ARIMA 학파에서 교육을 받은 경우, 최적의 AR 및 MA 순서를 선택하기위한 규정화된 지침을 외우고 있는 사람도 있을 것입니다. 모델 사양을 결정하기 위해 자동 상관 함수(ACF) 및 부분 자동 상관 함수(PACF)를 사용해야 합니다. 그러나 나는 그런 규정화된 지침을 잊어버리고 그냥 여러 순서의 후보 모델을 만들어 최적의 모델을 선택합니다. 왜 최상의 모델을 선택하기 위해 많은 모델을 생성하지 않을까요? 이러한 이유로, Python의 "pmdarima"와 같은 편리한 라이브러리가 있어 최적 사양을 자동화하는 데 도움이 됩니다. 이 장을 "자동 ARIMA"라고 제목 지어 이 이점을 강조하고자 합니다. 그래도 이 챕터에서는 차이, ACF 및 PACF의 개념을 다룰 것입니다.
"statsmodels"와 "pmdarima"와 같은 현대의 코드 라이브러리는 단기 예측이 아닌 다단계 예측을 가능하게 합니다. 이를 수행하기 위해 모델을 재귀적으로 적용하여 예측을 생성하는 방법에 대해 배우게 될 것입니다. 일반적으로 다단계 예측을 생성하는 두 가지 기본 전략이 있습니다: 재귀적 방법과 직접 방법. 우리는 챕터 13 "다단계 시계열 예측에 대한 튜토리얼"에서 이를 배울 것입니다. 두 전략은 ARIMA와 lightGBM 또는 XGB와 같은 트리 기반 모델에 채택되어 다단계 예측을 생성합니다.
마지막으로, 많은 사용 사례에서 우리는 점 추정치에 만족하지 않고 예측 구간을 필요로 합니다. 잠재적 불확실성을 평가하기 위해 가능한 값의 범위가 필요합니다. "pmdarima"와 "statsmodels"는 신뢰 구간을 반환합니다. 반면에, Part II "확률적 예측을 얻기"의 5부터 8 챕터에서 예측 구간을 위한 더 많은 기술을 배웠습니다.
- 제 5장: 시계열 확률 예측을 위한 몬테카를로 시뮬레이션
- 제 6장: 시계열 확률 예측을 위한 분위 회귀
- 제 7장: 시계열 확률 예측을 위한 형식 예측
- 제 8장: 시계열 확률 예측을 위한 형식화된 분위 회귀
이 글에서는 이론과 실무를 포괄적으로 설명하겠습니다. 실제 데이터를 사용하여 모델 구축과 예측을 안내할 예정이에요. 이미 알고 계신 부분은 건너뛰셔도 괜찮아요. Python 노트북은 여기서 다운로드할 수 있어요. 다룰 주제들은 다음과 같아요:
- ARIMA 모델
- 차분
- ACF 사용하여 MA의 차수 제안
- PACF 사용하여 AR의 차수 제안
- pmdarima 라이브러리 사용하여 최적 모델 자동 탐색
- 다단계 예측
- statsmodels 사용하여 모델을 반복적으로 업데이트
- SARIMA 모델
먼저 데이터를 불러오겠습니다.
데이터 전처리
카글의 아보카도 판매 데이터를 사용할 것입니다.
%matplotlib inline
from matplotlib import pyplot as plt
import pandas as pd
import numpy as np
from google.colab import drive
drive.mount('/content/gdrive')
path = '/content/gdrive/My Drive/data/time_series'
data = pd.read_csv(path + '/avocado_monthly.csv', index_col='Date')
data.sort_values(by='Total Volume', ascending=False)
(A) 그림은 이 데이터셋의 일부를 보여줍니다.
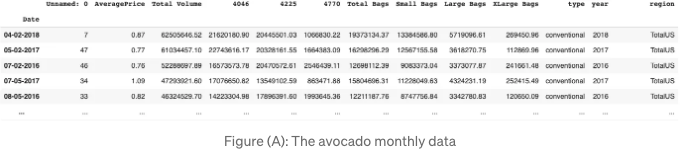
이 데이터 세트에서는 하나의 일변량 시계열만 사용할 것입니다.
# '유기농' 및 'TotalUS' 지역인 하나의 시계열만 사용합니다.
df = data[(data['type']=='organic') & (data['region']=='TotalUS')].copy()
df = df['Total Volume']
df.columns = ['y']
df = df[pd.to_datetime(df.index)<=pd.to_datetime('2018-02-01')]
# 일변량 시계열 그래프 그리기
plt.figure(figsize=(10,4))
plt.plot(df)
plt.xlabel("날짜")
plt.ylabel("볼륨")
plt.show()
그림 (B)는 일변량 시계열 그래프를 보여줍니다.
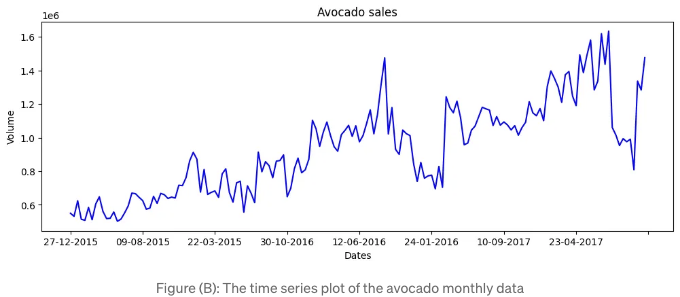
이후에는 80%를 인-타임 훈련 데이터로 사용하고 나머지 20%는 아웃-오브-타임 테스트 데이터로 사용합니다.
# Train-test-split
train_len = int(df.shape[0] * 0.8)
test_len = df.shape[0] - train_len
train, test = df[:train_len], df[train_len:]
print(f"{train_len}개의 훈련 샘플")
print(f"{df.shape[0] - train_len}개의 테스트 샘플")
좋아요. 이제 우리는 정의부터 시작합시다.
ARIMA 모델들
ARIMA는 단변량 시계열 데이터를 사용하여 미래 값을 예측하는 모델 클래스입니다. 이 모델들은 시계열 데이터의 과거 또는 이전 값, 즉 자기 회귀(AR) 항목과 이동 평균(MA) 항목인 이동 예측 오차의 지연된 값들을 사용하여 미래 값을 예측합니다. ARIMA이란 "자기 회귀-통합-이동 평균"의 약자로, "AR", "I", "MA"로 구성됩니다. 여기서 ARIMA의 "I"는 "통합(integrated)"을 의미하며, 이는 시계열 데이터가 안정성을 달성하기 위해 차분된 것을 나타냅니다. 안정적인 시계열 데이터는 시간이 지나도 평균, 분산 및 자기 상관이 일정하므로 모델링하기 쉽습니다. ARIMA(p,d,q) 모델로 수학적으로 표현하면 다음과 같습니다:
Markdown 형식으로 테이블 태그를 변경하십시오.
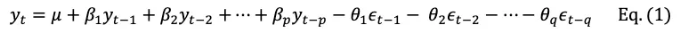
ARIMA 표기법에 친숙해지기 위해 위 식을 적용해 봅시다.
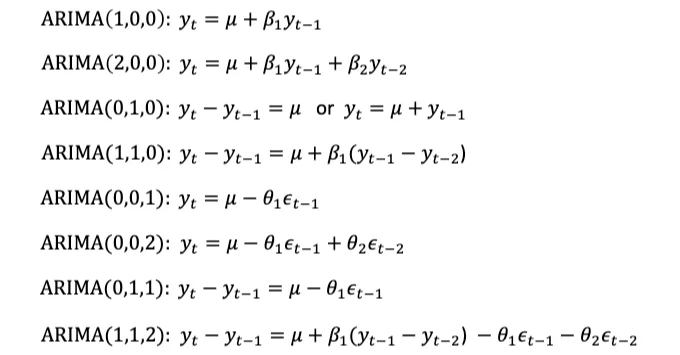
일반적으로 AR만 또는 MA만, 또는 p와 q가 모두 4 미만이기 때문에 우변에 많은 항이 없습니다.
차이화
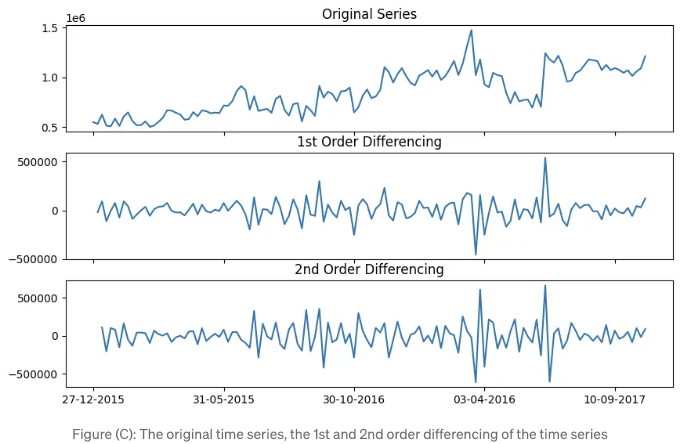
차이화의 목표는 시계열을 안정적으로 만드는 것입니다. 시계열에서 안정성이란 값의 평균이 시간에 따라 일정하다는 것을 의미합니다. 다시 말해, 안정적인 시계열은 일정한 평균을 갖습니다. 이전 코드는 원래 시계열, 1차 차이화(한 번 차이화), 그리고 2차 차이화(두 번 차이화)를 플롯합니다.
import numpy as np, pandas as pd
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
from statsmodels.tsa.stattools import adfuller
import matplotlib.pyplot as plt
plt.rcParams.update({'figure.figsize':(10,6), 'figure.dpi':100})
lag_len = 15
fig, axes = plt.subplots(3, 1, sharex=True)
# Original Series
axes[0].plot(train.values); axes[0].set_title('Original Series')
# 1st Differencing
axes[1].plot(train.diff()); axes[1].set_title('1st Order Differencing')
# 2nd Differencing
axes[2].plot(train.diff().diff()); axes[2].set_title('2nd Order Differencing')
axes[0].xaxis.set_major_locator(MultipleLocator(30))
plt.show()
도 (C)는 학습 데이터의 원래 시계열, 1차 차이화, 그리고 2차 차이화에 대한 플롯을 보여줍니다. 1차 및 2차 차이화된 시계열은 안정적입니다. 즉, 모델은 최소한 한 번은 차이화되어야 합니다. 일반적으로 1차 차이화만으로 충분합니다. 안정적인 시계열에 대한 차이화는 여전히 안정적일 것입니다. 1차 차이화가 이미 안정적이라면 2차 차이화를 얻기 위해 과도하게 차이화할 필요가 없습니다.
이제 ACF를 사용하여 MA(order)를 얻는 방법에 대해 이해해 봅시다.
ACF를 사용하여 MA(order)를 제안합니다.
이미 두 변수 간의 상관 계수에 익숙하실 것입니다. 이는 그들의 관계를 측정합니다. -1과 1 사이의 값을 갖습니다. 양의/음의 상관 계수는 두 변수 간에 양의/음의 관계가 있음을 의미합니다. 상관 계수가 1일 경우 완벽한 양의 선형 관계를, 0.0일 경우 변수 간의 선형 관계가 없음을 나타냅니다.
ACF는 자기상관함수(Autocorrelation Function)의 약자입니다. 이것은 시계열과 그 지연된 버전 간의 상관관계를 측정합니다. ACF는 시계열의 시간 t와 시간 t-k에서의 값들 간의 상관관계로 계산됩니다. 여기서 k는 래그(지연) 번호를 나타냅니다. ACF(k)는 래그 k에서의 자기상관을 나타냅니다. 자기상관을 시각화해봅시다.
from statsmodels.graphics.tsaplots import plot_acf
plt.rcParams.update({'figure.figsize':(10,6), 'figure.dpi':100})
lag_len = 15
fig, axes = plt.subplots(3, 1, sharex=True)
# 원 데이터
plot_acf(train.values[0:lag_len], ax=axes[0], title = 'ACF - 원 데이터')
# 1차 차분
plot_acf(train.diff().dropna()[0:lag_len], ax=axes[1], title = 'ACF - 1차 차분')
# 2차 차분
plot_acf(train.diff().diff().dropna()[0:lag_len], ax=axes[2], title = 'ACF - 2차 차분')
plt.show()
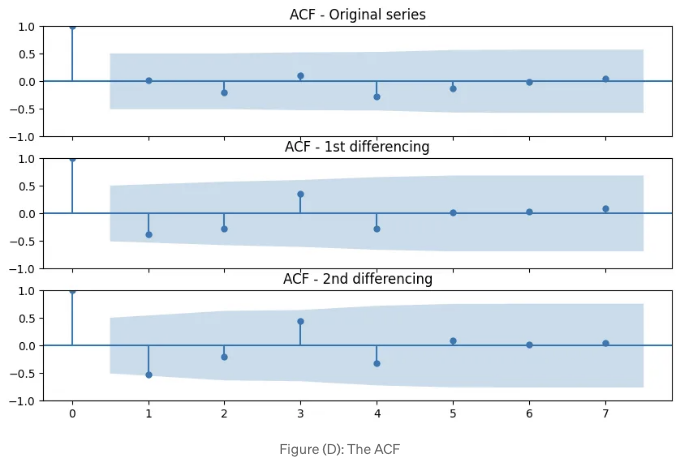
(D) 그림은 자기상관을 보여줍니다. 첫 번째 막대의 상관 계수는 1.0인데, 이는 y_t와 그 자신의 상관관계를 나타냅니다. 파란 영역은 유의수준을 의미합니다. 유의수준을 넘는 막대는 통계적으로 유의미하다는 것을 의미합니다. 보시다시피, 1차 차분 라인에서의 래그 1은 유의미합니다. 이는 모델이 래그 1 항을 포함하고 있으며 1차 차분이 있다는 것을 의미합니다.
이제 PACF를 배워 봅시다.
PACF를 사용하여 AR의 순서를 제안하세요.
ACF는 시계열과 그 이전 시간 단계의 관련성을 측정합니다. 현재 시계열 값이 과거 값들과 얼마나 연관이 있는지를 알려줍니다. 반면 PACF는 시계열과 그 이전 시간 단계의 부분 상관 관계를 측정하며, 해당 시간 단계 이전의 모든 이전 시간 단계 값을 고려한 후의 영향을 고려합니다. 이는 현재 시계열 값과 특정 시간 지연 값 사이의 직접적인 관계가 있는지 여부를 결정하는 데 도움이 됩니다. 특히 (E) 그림에서 PACF 지연 1이 중요하다고 합니다. 이는 유의 수준을 넘어섰기 때문입니다. 지연 2도 중요하다고 판명되었는데, 약간의 노력으로 유의 선을 넘었습니다(파란색 영역).
from statsmodels.graphics.tsaplots import plot_pacf
plt.rcParams.update({'figure.figsize':(10,6), 'figure.dpi':100})
lag_len = 15
fig, axes = plt.subplots(3, 1, sharex=True)
# Original Series
plot_pacf(train.values[0:lag_len], ax=axes[0], title = 'PACF - Original series')
# 1st Differencing
plot_pacf(train.diff().dropna()[0:lag_len], ax=axes[1], title = 'PACF - 1st differencing')
# 2nd Differencing
plot_pacf(train.diff().diff().dropna()[0:lag_len], ax=axes[2], title = 'PACF - 2nd differencing')
plt.show()
(E) 그림은 PACF 플롯을 보여줍니다.
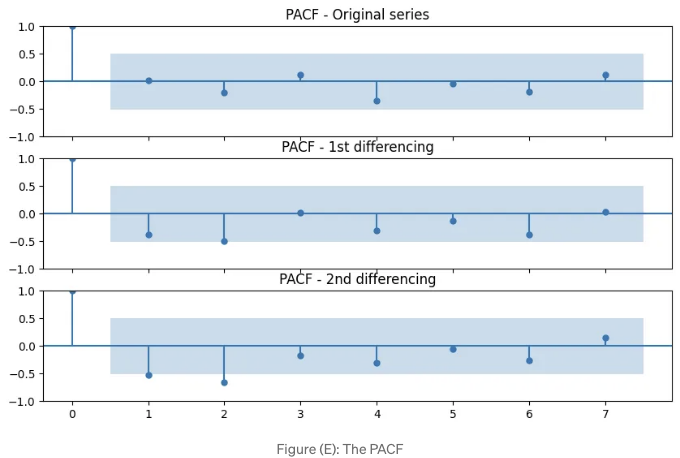
그림 (C), (D), (E)의 차이, ACF 및 PACF는 ARIMA(1, 1, 1)을 제안합니다. 만약 이 진단을 알지 못한다고 가정하더라도, 여전히 auto_ARIMA()를 사용하여 모델 사양의 범위를 찾을 수 있습니다.
auto_ARIMA() 사용하여 최적 모델을 자동으로 탐색하는 방법
import pmdarima as pm
model = pm.auto_arima(train,
d=None,
seasonal=False,
stepwise=True,
suppress_warnings=True,
error_action="ignore",
max_p=None,
max_order=None,
trace=True)
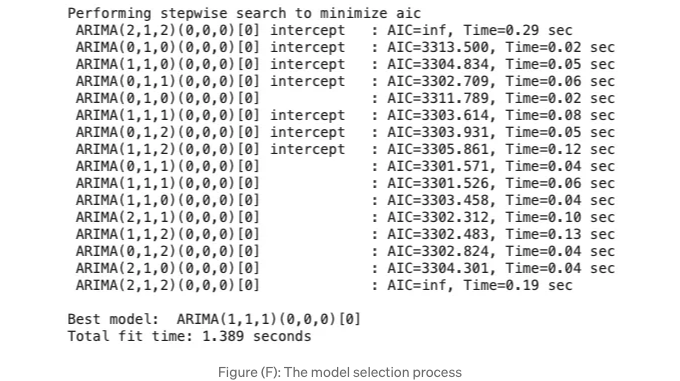
아카이케 정보 기준(Akaike Information Criterion, AIC) 값은 모델 성능 지표입니다. 이 값은 2 * 모델 파라미터 수 - 2 * 최대 우도(L)입니다. 값이 작을수록 모델이 더 잘 맞는 것을 나타냅니다.
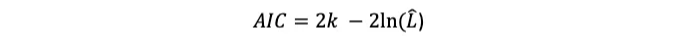
Figure(F)에서 가장 낮은 AIC 값은 3,301.526입니다. ARIMA(1, 1, 1)(0, 0, 0)입니다. 계절성 구성요소는 (0, 0, 0)입니다. 계절 차분이 없기 때문에 "seasonal=False"로 하이퍼파라미터를 끔 처리했습니다. 나중에 ARIMA에서 다시 활성화할 것입니다.
다중 기간 예측
"pmdarima"의 "predict" 함수를 사용하면 미래 시점의 기간 수를 지정할 수 있습니다. 미래 시점을 테스트 데이터의 길이로 설정합니다. 그리고 "return_conf_int = True"와 "alpha = 0.05"로 설정하여 95% 신뢰 수준의 신뢰 구간을 반환합니다.
# test_len의 길이에 대한 다중 기간 예측 생성
fcast = model.predict(n_periods=test_len, return_conf_int=True, alpha=0.05)
forecasts = fcast[0]
confidence_intervals = fcast[1]
모델의 성능을 평가해 봅시다.
from sklearn.metrics import mean_squared_error, mean_absolute_percentage_error
print(f"MAPE: {mean_absolute_percentage_error(test, forecasts)}")
평균 절대 백분율 오차는 0.1490595592393948 또는 14.9% 입니다. 다음으로 실제 값과 예측값을 그래프로 그려보겠습니다.
def plot_it():
fig, ax = plt.subplots(figsize=(12,4))
# 실제 vs. 예측
ax.plot(train, color='blue', label='Training data')
ax.plot(test.index, forecasts, color='red', marker='o',
label='Predicted')
ax.plot(test.index, test, color='green', label='Test data')
ax.set_title('아보카도 판매량')
ax.set_xlabel('날짜')
ax.set_ylabel('양')
conf_int = np.asarray(confidence_intervals)
# 신뢰 구간
ax.fill_between(test.index,
conf_int[:, 0], conf_int[:, 1],
alpha=0.9, color='orange',
label="신뢰 구간")
# 주요 눈금이 20의 배수인 플롯 생성
ax.legend()
ax.xaxis.set_major_locator(MultipleLocator(20))
plt.show()
plot_it()
표 (G)는 학습, 테스트 데이터, 예측값 및 신뢰 구간의 시계열을 제공합니다.
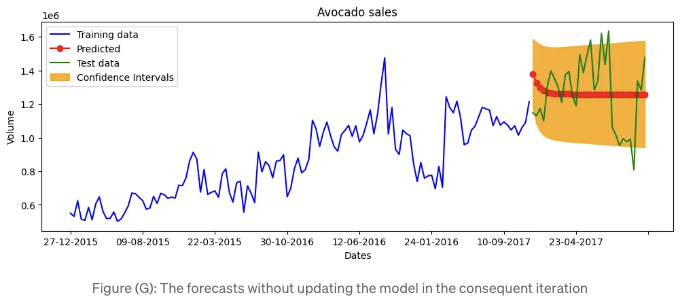
표 (G)의 예측 값은 일정 기간 이후에 고정값에 수렴하며 예측 가능성이 있습니다. 인상적으로 보이지 않습니다. 각 반복에서 모델을 업데이트하여 개선할 수 있습니다.
각 반복에서 모델을 업데이트해보세요.
각 예측은 예측 시계열에 새로운 관측치를 추가합니다. 모델이 정적인 경우, 예측된 시계열은 최종적으로 직선이 되어 그래프(G)에 표시됩니다. 각 반복에서 추가된 관측치로 모델을 업데이트할 수 있습니다.
우리는 시간 외 시험 기간의 각 반복에서 한 기간을 예측한 후, 새로운 예측을 모델을 업데이트하는 데 사용할 것입니다. "return_conf_int = True" 및 "alpha= 5%"를 지정하여 95% 신뢰 수준의 예측 구간을 추가할 수 있습니다.
# https://alkaline-ml.com/pmdarima/modules/generated/pmdarima.arima.ARIMA.html#pmdarima.arima.ARIMA.update
def one_period_forecast():
fcast = model.predict(n_periods=1, return_conf_int=True, alpha=0.05)
# fcast는 두 개의 리스트로 구성됩니다.
# 첫 번째 리스트는 예측입니다.
forecasts = fcast[0].tolist()
# 두 번째 리스트는 신뢰 구간입니다.
confidence_intervals = fcast[1]
return ( forecasts,
np.asarray(confidence_intervals).tolist()[0])
forecasts = []
confidence_intervals = []
for add_obs in test:
fc, conf = one_period_forecast()
forecasts.append(fc)
confidence_intervals.append(conf)
# 기존 모델 업데이트
model.update(add_obs)
plot_it()
그림 (H)은 예측값이 테스트 값과 더 잘 일치함을 보여줍니다.
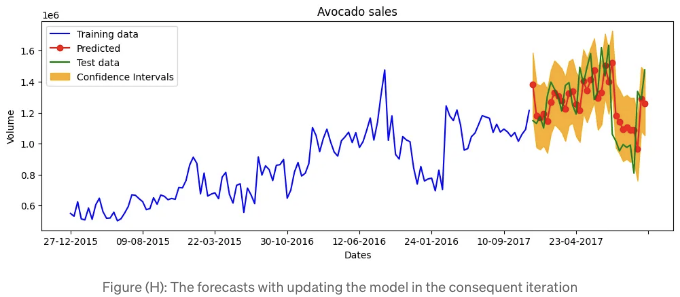
모델 성능은 어떤가요?
print(f"MAPE: {mean_absolute_percentage_error(test, forecasts)}")
MAPE는 0.11766234388644323으로, 약 11.7%보다 약간 향상되었습니다.
우리 연구를 위한 데이터는 여러 해에 걸친 시계열 데이터이기 때문에 강력한 계절성을 갖고 있다고 의심됩니다. 우리는 Seasonal ARIMA를 사용하여 모델을 완화할 것입니다.
SARIMA 모델
SARIMA 모델은 계절적 시계열 데이터를 다루는 데 특히 설계되었습니다. ARIMA 모델의 비계절적 구성요소 (AR, I 및 MA)에 추가로 SARIMA 모델에는 데이터의 계절적 패턴을 포착하는 계절적 구성요소 (SAR, SI 및 SMA)가 포함되어 있습니다. SARIMA 모델의 SAR 구성요소는 ARIMA 모델의 AR 구성요소와 유사하지만 시계열의 계절적 지연된 값에 작용합니다. SI 구성요소는 ARIMA 모델의 I 구성요소와 유사하지만 시계열의 계절적 차이에 적용됩니다. 마지막으로, SMA 구성요소는 ARIMA 모델의 MA 구성요소와 유사하지만 시계열의 계절적 지연된 오차에 작용합니다.
요약하자면, SARIMA는 단순히 계절 급변을 적용합니다. 계절적 급변은 일반적인 급변과 유사합니다. 연이은 용어를 빼는 대신, 계절적 급변은 이전 계절의 값에서 값을 뺍니다. SARIMA 모델은 일반적으로 SARIMA(p,d,q)(P,D,Q)[S]로 표기됩니다.
- p은 계절적 자기회귀항의 차수를 나타냅니다.
- q는 계절적 이동평균항의 차수를 나타냅니다.
- Q는 계절적 차분의 차수를 나타냅니다.
- S는 12개월과 같은 계절 사이클을 나타냅니다.
계절 ARIMA 모델은 데이터의 계절 패턴을 포착하기 위해 추가 매개변수를 통합합니다. 다음 구성 요소를 추가합니다:
- 계절적 AR 항: 이러한 항목은 현재 관측치와 계절 간격의 특정 차이 관측치 사이의 관계를 나타냅니다. 데이터의 계절적 패턴을 캡처합니다.
- 계절적 MA 항: 이러한 항목은 현재 관측치와 계절 간격의 특정 기간의 선행 예측 오류 사이의 관계를 나타냅니다. 데이터의 계절적 변동성을 캡처합니다.
SARIMA 모델링은 매우 쉽습니다. 해야 할 일은 하이퍼파라미터 "seasonal"을 "True"로 변경하는 것뿐입니다.
import pmdarima as pm
model = pm.auto_arima(train,
# You just need to turn the seasonal to "True"
seasonal=True,
start_P=1,
start_q=1,
max_p=None,
max_q=None,
m=12,
d=1,
D=1,
trace=True,
error_action='ignore',
suppress_warnings=True,
stepwise=True)
model.summary()
한 가지 모델을 만들었어요. 그림 (I)은 최적의 모델이 ARIMA(0,1,1)(0,1,1)[12]임을 보여줍니다.

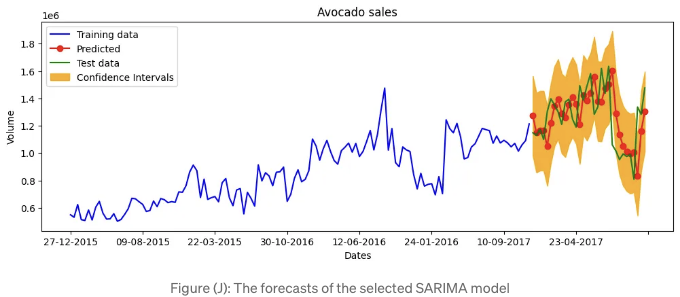
결과를 그래픽으로 표시하고 각 반복마다 모델 업데이트를 활성화해봅시다. 그림 (J)에 플롯이 표시됩니다.
forecasts = []
confidence_intervals = []
for add_obs in test:
fc, conf = one_period_forecast()
forecasts.append(fc)
confidence_intervals.append(conf)
# Updates the existing model
model.update(add_obs)
# Plot the results
plot_it()
# Calculate MAPE
print(f"MAPE: {mean_absolute_percentage_error(test, forecasts)}")
MAPE는 0.11918293096560012 또는 11.9%입니다. 이것은 위의 ARIMA 모델에 비해 뚜렷한 개선이 없어 보입니다. 모델의 간결성 원칙에 따라, 우리는 SARIMA 대신 ARIMA 모델을 사용할 것입니다.
결론
이 게시물에서는 고전적인 ARIMA 및 SARIMA 모델 사양을 검토했습니다. 최적 모델을 자동으로 검색하기 위해 pmdarima 라이브러리의 사용법을 배웠습니다. 또한 ARIMA 및 SARIMA에 대한 다기간 예측 생성 방법을 배웠습니다.
우리는 복잡성이 증가하는 시계열 데이터를 모델링할 것입니다. 여러 Python 라이브러리가 복잡한 데이터 구조에 대한 해결책을 제공합니다. 우리는 이러한 데이터 솔루션을 10장에서 배울 것입니다: 시계열 데이터 형식 변환의 비밀.
참고문헌
- [1] Box, G. E. P., Jenkins, G. M., and Reinsel, G. C. (2015). 시계열 분석: 예측 및 제어 (5판). John Wiley & Sons.
샘플 eBook 챕터(무료): 여기
- 아름다운 형식으로 책을 재현하고 즐거운 독서 경험을 제공하기 위해 The Innovation Press, LLC 직원 여러분께 감사드립니다. 우리는 Teachable 플랫폼을 선택하여 전 세계 독자들에게 번거로운 과부하 없이 eBook을 유통합니다. 신용 카드 거래는 Teachable.com이 안전하고 기밀리에 처리합니다.
Teachable.com의 eBook: $22.50 여기
Amazon.com에서 인쇄판: $65 링크
- 프린트 버전은 윤광 처리 커버, 컬러 인쇄, 아름다운 스프링어 글꼴 및 레이아웃을 채택하여 즐거운 독서 경험을 제공합니다. 7.5 x 9.25인치의 품격 높은 크기는 서재에 있는 대부분의 책과 어울립니다.
- "이 책은 Kuo의 시계열 분석에 대한 깊은 이해와 예측 분석 및 이상 탐지에 대한 응용을 증명하는 것입니다. 이 책은 독자들이 실제 세계의 문제에 대처하기 위한 필수적인 기술을 제공합니다. 데이터 과학 분야로의 직업 전환을 고려하는 사람들에게 특히 가치 있는 자료입니다. Kuo는 전통적인 기술 뿐만 아니라 최신 기술에 대해 자세히 탐구합니다. Kuo는 신경망 및 다른 고급 알고리즘에 대한 논의를 통합하여, 분야의 최신 동향과 발전을 반영합니다. 이는 독자가 확립된 방법뿐만 아니라 데이터 과학 분야에서 가장 현재이고 혁신적인 기술을 다루는 데 대비할 수 있도록 보장합니다. Kuo의 생생한 글쓰기 스타일로 책의 명료함과 접근성은 높아졌습니다. 그는 복잡한 수학 및 통계 개념을 신비롭지 않게 만들면서도 엄격성을 희생하지 않았습니다."
현대적인 시계열 예측: 예측 분석 및 이상 탐지를 위한
제로 장: 서문
1장: 소개
장 2: 비즈니스 예측을 위한 선지자
장 3: 튜토리얼 I: 트렌드 + 계절성 + 휴일 및 이벤트
장 4: 튜토리얼 II: 트렌드 + 계절성 + 휴일 및 이벤트 + 자기회귀(AR) + 지연 회귀자 + 미래 회귀자
장 5: 시계열 데이터의 변화점 탐지
Chapter 6: 시계열 확률 예측을 위한 몬테카를로 시뮬레이션
Chapter 7: 시계열 확률 예측을 위한 분위 회귀
Chapter 8: 시계열 확률 예측을 위한 일치 예측
Chapter 9: 시계열 확률 예측을 위한 일치화된 분위 회귀
제 10장: 자동 ARIMA!
제 11장: 시계열 데이터 형식 쉽게 만들기
제 12장: 다기간 확률 예측을 위한 선형 회귀
제 13장: 트리 기반 시계열 모델을 위한 피처 엔지니어링
14장: 다기간 시계열 예측을 위한 두 가지 기본 전략
15장: 다기간 시계열 확률적 예측을 위한 Tree 기반 XGB, LightGBM 및 CatBoost 모델
16장: 시계열 모델링 기술의 진화
17장: 시계열 확률적 예측을 위한 Deep Learning 기반 DeepAR
Chapter 18: 주가에 대한 확률적 예측을 위한 응용
Chapter 19: RNN부터 Transformer 기반 시계열 모델까지
Chapter 20: 해석 가능한 시계열 예측을 위한 Temporal Fusion Transformer
Chapter 21: 시계열 예측을 위한 오픈소스 Lag-Llama 튜토리얼