백만 달러의 방정식: 옵션 가격에 대한 블랙-숄즈 모델입니다. 금융 분야에서 일하거나 공부한 적이 있다면, 아마도 이 이름을 듣거나 귀띔해 본 적이 있을 것입니다. 전문화 수준에 따라 옵션의 가격을 근사하거나, 투자 결정을 내리는 데 직접 사용했을 수도 있습니다. 다음과 같은 방정식 중에서 가장 익숙한 것은 다음과 같을 것입니다:
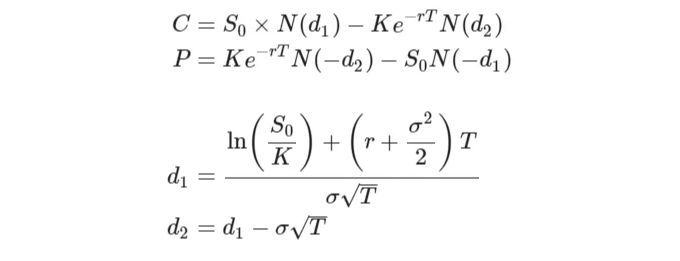

비록 다소 복잡한 방정식으로 보일 수 있지만, 원칙적으로는 실제로 사용하기 굉장히 간단합니다: 플러그 앤 플레이 방식이죠. 매개변수를 알고 있거나 추정할 수 있다면, 방정식에 그 값들을 넣어서 콜옵션이나 풋옵션의 해당 가격을 얻을 수 있습니다. 그리고 이 정보를 활용해서 시장 가격과 비교하거나, 다양한 매개변수로 다양한 투자 시나리오를 시뮬레이션하고, 떠오르는 모든 아이디어들을 실행할 수 있습니다.
그렇지만 만약 저처럼 좀 호기심 많은 사람이거나, 양자 분야에 관심이 있거나, 양자 세계에 진출하고 싶다면 한 가지 의문을 품고 계셨을 것입니다: 이 방정식은 어째서 나왔는 걸까요?
본 문서에서는 양자의 시각에서 블랙-숄즈 모델에 대한 깊은 탐구를 할 것입니다. 주의: 앞으로 많은 수학이 나옵니다! 만약 실용적인 투자 기술을 찾고 있다면, 유감스럽지만 이 글은 아닙니다. 그러나 양자 인터뷰를 준비하고 있거나, 양자금융에 관심이 있으며 주제에 대한 깊은 이해를 원한다면 당신을 위한 이야기가 될 것입니다. 확률 미적분 및 금융 수학에 대한 일정 수준의 지식이 필요합니다. 함께 시작해봐요!
블랙-숄즈 SDE
옵션 가격 측정에 들어가기 전에, Black-Scholes 모델에서 가정된 기초 자산 가격 프로세스의 확률적 동역학을 먼저 살펴봅시다:
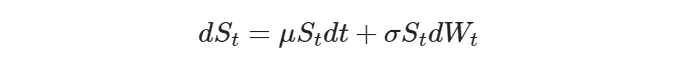

이 확률적 미분 방정식(SDE)을 이해하는 방법은 다음과 같습니다: 기초 자산 S의 가격(LHS)의 연속적인 변화는 결정적 시간 구성요소(드리프트)와 확률적 구성 요소(확산)에 의존합니다. 이 가격 모델은 기하 브라운 운동(GBM)으로도 알려져 있습니다. 비교적 간단하지만 올바르게 사용할 때 시장에서 관측되는 가격과 유사한 확률 과정을 근사화해줍니다.
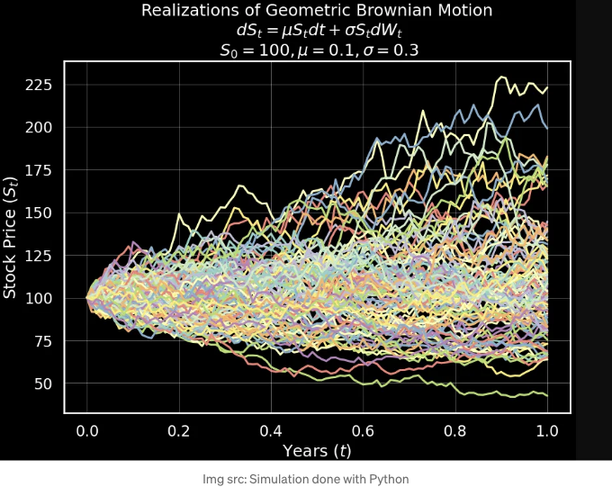
특정 시간 t에서의 가격에 대한 명시적 공식을 유도할 수 있다는 사실을 알 수 있습니다:
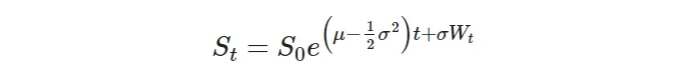
이 형태에서 브라운 운동의 특성을 기반으로 분포를 추론할 수 있습니다. 그러나 이 공식을 어떻게 얻을 수 있을까요? 여기서 우리의 친구인 확률 미적분학의 이토 레마가 도움이 됩니다.
Black-Scholes SDE 해결하기
SDE를 해결하기 위해서 가장 사용하기 좋은 도구는 보통 이토의 렘마입니다. 이토 프로세스를 고려해 봅시다:
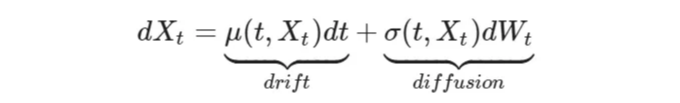
이전과 매우 유사한 가격 역학을 보여주지 않나요? 이토의 렘마는 다음과 같이 규정합니다:
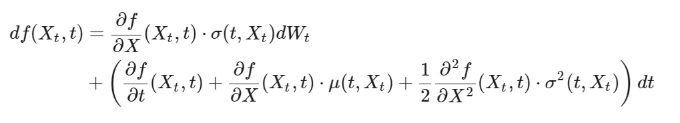
따라서 우리가 연속적이고 두 번 미분 가능한 함수 f의 올바른 선택을 찾을 수 있다면 S_t에 대한 식을 구할 수 있습니다. 이전의 SDE를 한 번 더 살펴봅시다:
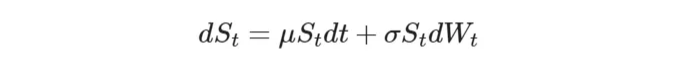
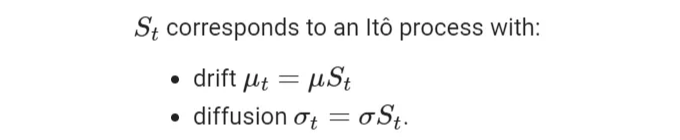
Ito의 보조정리를 적용하면 f(s) = ln(s)일 때,
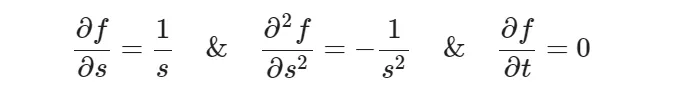
에서 우리가 사용해야 하는 도함수들이 있습니다. 이를 공식에 대입하고 간소화하면 다음과 같은 해답이 도출됩니다:
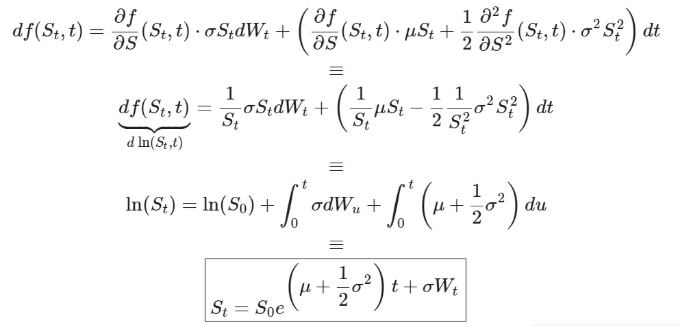
이곳에서 하는 일은 모든 용어를 매칭하고 미분을 대체하는 것입니다. 세 번째 줄에서는 어디에나 적분을 한 다음 남은 적분을 해결합니다. 브라운 운동에 대한 적분은 W_u에 의존하지 않습니다. 따라서 그 자체로 B.M.이 됩니다. 확률적 적분 및 미분에 익숙하지 않다면 Quantstart의 멋진 글을 읽어보세요.
결과적인 가격의 중요한 특성 중 하나는 로그-정규 분포를 따른다는 것이며, S_t의 로그가 정규 분포를 따른다는 것으로 나타낼 수 있습니다:
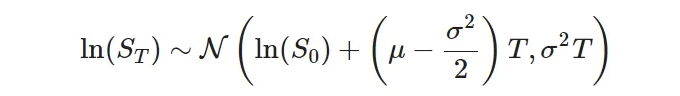
추신으로, 로그 수익도 정규 분포를 따릅니다:
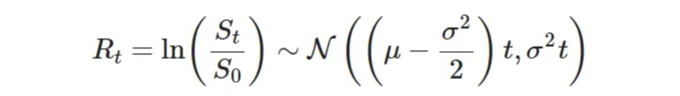
Although I won’t go through the derivations here, this will be important in deriving the actual Black-Scholes pricing formulas that we saw at the beginning.
Risk-Neutral Stochastic Dynamics
When pricing derivatives, financial mathematics and stochastic calculus tell us that we can assume that all assets grow and can be discounted at the risk-free rate, giving a “fair price”. To understand how this works from a practical point of view, I recommend reading this article. From a theoretical perspective, this corresponds to the The First Fundamental Theorem of Asset Pricing. Thus, in order to price anything, we need to transform our price model to the risk-neutral world.
두 가지 주요 개념을 기억해 봅시다: Radon-Nykodym 도함수 과정과 Girsanov의 정리.

Measure 변경 정리는 위의 속성을 가진 확률 변수가 존재하여 실제 확률 측도 P를 기반으로 한 확률 측도 Q("리스크 중립" 측도)를 구성할 수 있다는 것을 말해줍니다. 그러나 이것을 일반적인 확률 과정에 확장하는 방법은 어떻게 될까요? 다음 정리는 Radon-Nykodym 도함수를 기반으로 한 과정의 존재를 알려줍니다:

본 정의는 각 시간 단계 t에서 Radon-Nykodym 도함수가 적용되며, 더 나아가 이 도함수는 항상 마팅게일입니다.
그래서 이제 위험 중립적 측도로 전환하기 위해 이러한 확률과정이 존재한다는 걸 알게 되었는데, 정확히 어떻게 이 변화를 수행해야 할까요? Girsanov의 정리는 이 구성을 제공하고 결과적인 과정이 여전히 유효한 마틴게일임을 보장합니다. 이는 금융 수학 분야의 여러 응용프로그램에 필수적인 조건으로, 특히 이 연구와 같은 위험 중립 파생상품 가격 산출에 적용됩니다.

이제 우리의 문제에 이를 어떻게 적용하는지 살펴봅시다. 원래의 실세계 측도 P 하에서의 원래 동역학을 상기해보세요:
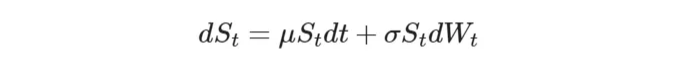
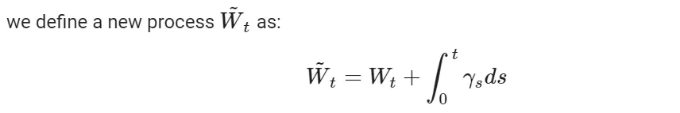

To achieve this, we set
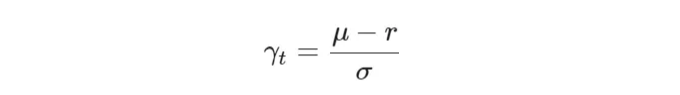
By plugging this into the measure and with some simple manipulations, the dynamics of S_t under the risk-neutral measure Q become:
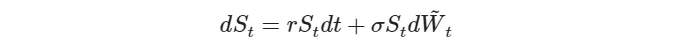
Also, we have by Girsanov’s that

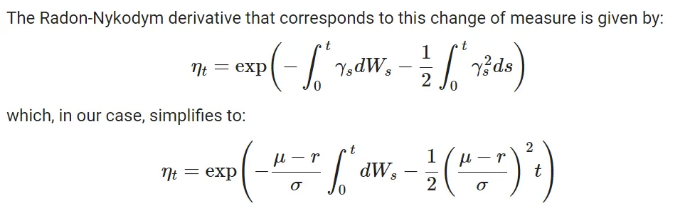
따라서, Girsanov의 정리는 위험 중립 측도 Q 하에서 할인된 프로세스가 Martingale임을 보장합니다. 이로부터 금융 수학의 여러 정리와 결과를 통해 위험 중립 동역학 하에서 파생상품을 가격 지정할 때 "공정 가격"을 찾을 수 있다.
옵션 프로세스의 블랙-숄즈 모델 도출
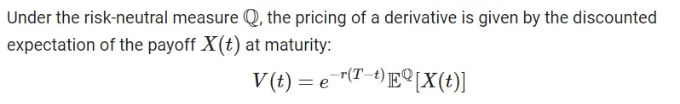
The idea is pretty clear: if we want to price a derivative say, at inception (t=0) it’s value should be the potential (expected) payoff we should get from it at maturity, adjusted via the risk-free rate today.
Thus, for an European Call and Put option at time t from inception respectively is given by:
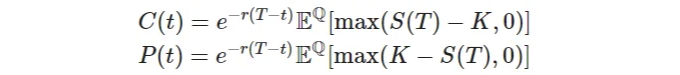
위의 표를 다음과 같이 마크다운 형식으로 변경해주세요.
Notice that the expectation is taken under the risk-neutral measure. In order to solve this expectation, let’s revisit the stochastic dynamics and distribution for S(T):
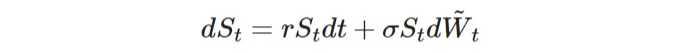
which implies that
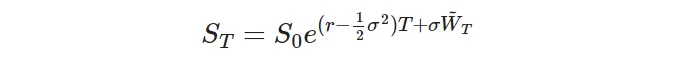
위에서 W_T에 물결표시(~)가 있는 경우, 그것은 위험중립 측도 아래의 브라운 운동입니다.
이제 위험중립 측도 아래 콜 옵션의 페이오프의 기대값은 다음과 같습니다:
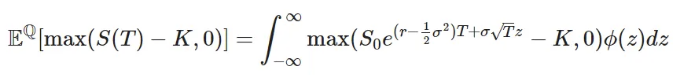
여기서 함수 phi(z)는 표준 정규 분포의 확률밀도함수입니다.
이제 호출 옵션이 가치를 가지는 경우는 있음을 주목해 주세요.
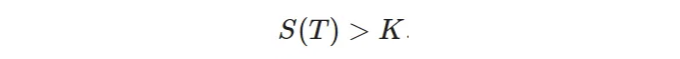
이 조건은 다음과 같이 번역됩니다.
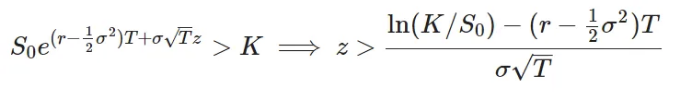
따라서, 적분에서 값의 오른쪽 위 부분만 0이 아닙니다:
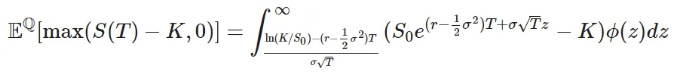
다음으로, 적분을 두 부분으로 나눌 수 있다는 것에 유의하세요:

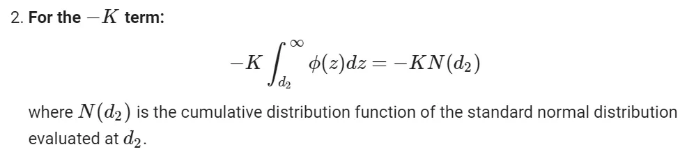
Combining the both parts and applying the discount factor we obtain:
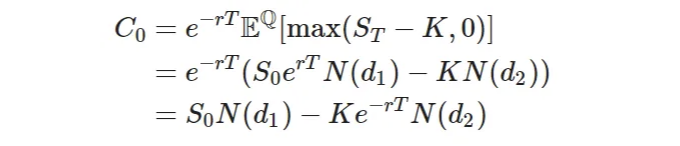
, where
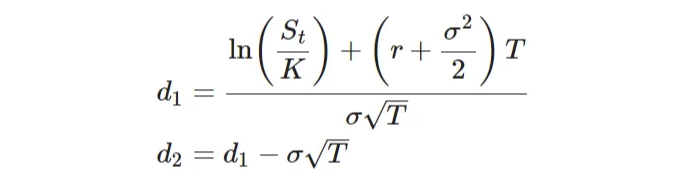
, 이것은 잘 알려진 Black-Scholes 공식입니다. Put에 대한 유도는 유사하지만, Put-Call Parity가 항상 성립한다는 것을 기억하세요, 즉:
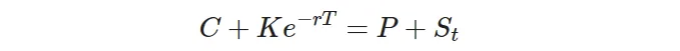
Black-Scholes PDE
우리가 블랙-숄즈 모델에 대한 수학적 분석을 완료한 것은 아직이에요. 위키백과의 글을 확인하면 다음과 같은 방정식을 만나게 될 거에요:
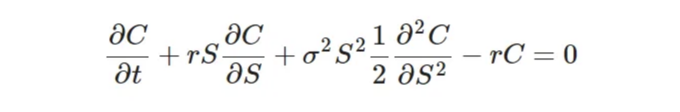
이 방정식이 의미하는 바를 이해하고 해석하는 방법을 이해하려면, 재무 해석을 통해 확률 해석을 통한 유도를 살펴보는 게 좋아요:

아래와 같이 도함수(derivatives)가 제공됩니다:
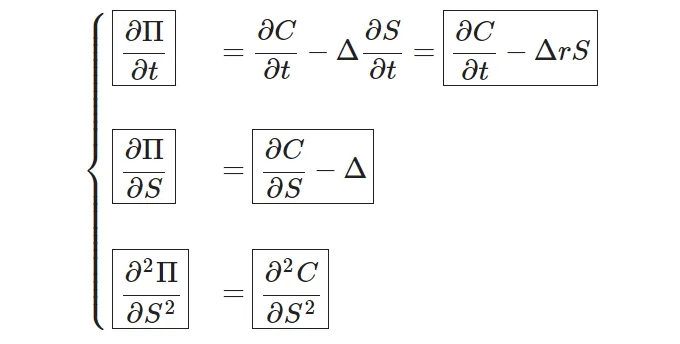
따라서:
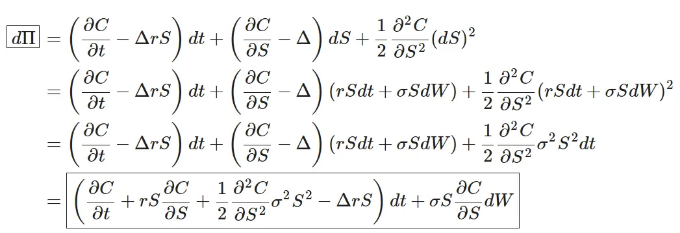
, 세 번째 단계는 다음 사실에서 나온다.
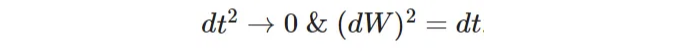
포트폴리오가 자율자금화되어 있으며(즉, 초기 자본 외에는 자본을 투입하지 않는다) 무위험이어야 하므로(어떠한 황폐도도 없음), 포트폴리오 가치의 변화는 무위험 이자율에 초기 포트폴리오 가치를 곱한 것이어야 한다:
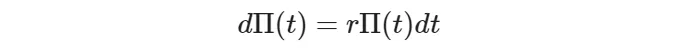
이제, 기억하시나요?
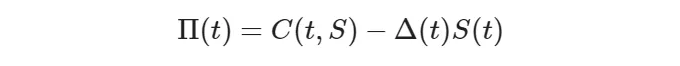
이전 방정식에 대체하면,

아래는 블랙-숄즈 PDE의 정확한 수식입니다. 따라서, 우리는 우리가 가정한 확률 동역학과 무위험 및 위험 중립 원칙에서 완전히 유도된 이 방정식을 명확히 볼 수 있습니다.
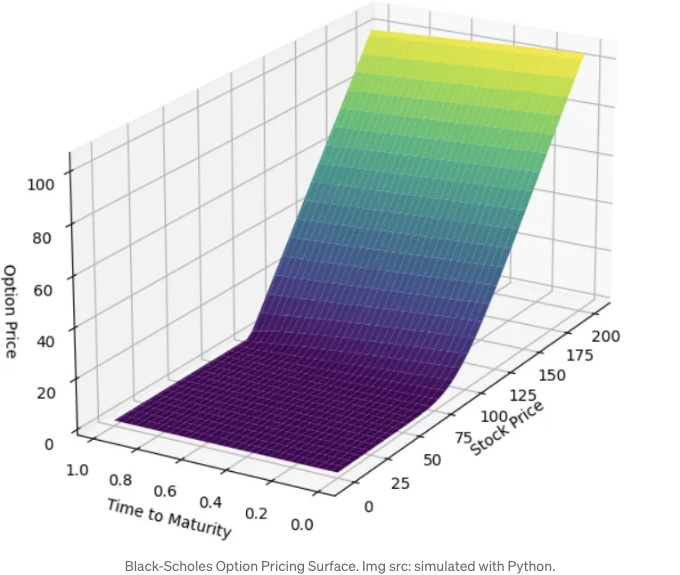
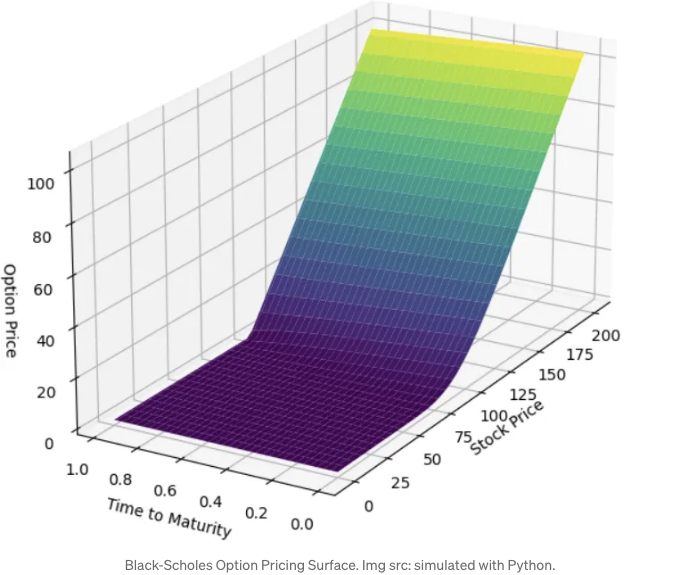
블랙-숄즈 가격 표면
보너스로 블랙-숄즈 가격 결정 표면을 시각화할 수 있습니다. 이것은 글의 시작 부분에서 보았던 것입니다. 아래는 그림을 생성하는 코드입니다:
그리스
블랙-숄즈 편미분 방정식에서 중요한 파생 변수 몇 가지를 분석할 수 있습니다. 이는 일반적으로 그리스(Greeks)라고 알려진 것들입니다. 그리스는 블랙-숄즈 방정식에서 직접 취할 수 있거나 유래된 구성 요소들로, 옵션 가격 공식의 도함수는 옵션 가격 및 다른 것들이 다른 매개변수가 변할 때(나머지는 일정한 상태에서) 어떻게 변하는지 알려줍니다. 이것은 별도의 주제이므로, 오늘은 델타, 감마, 세타 및 베가에 대한 개요, 그리고 옵션 포트폴리오에서 처음 두 가지를 헷징하는 방법에 대해서만 다룰 것입니다.
아래 내용을 따를 때 Black-Scholes 옵션 가격 산식을 상기해 봅시다:
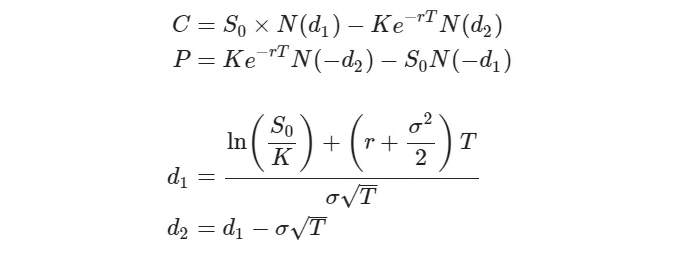

옵션의 델타는 옵션 가격이 기초 자산 가격의 변화에 대해 변하는 속도를 측정합니다. 수학적으로, 다음과 같이 쉽게 볼 수 있습니다:
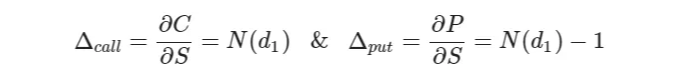
As a side note, for a portfolio of options, the delta of the portfolio is simply the aggregated deltas in that porfolio:
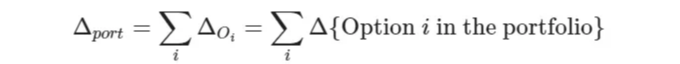
The question is: what do we do with this information?
델타 헷지

이제 이에 대한 구체적인 예시를 살펴보겠습니다:

헷지를 적용하면 포트폴리오 가치가 대부분 일정하게 유지되는 것을 확인할 수 있어요! 헷지 없이는, 옵션의 변동폭이 0.04달러가 아닌 0.56달러가 될 거예요!
파이썬 예제로 설명해볼게요:
시나리오 1 (S_new = 50):
델타 헷지 없이 포트폴리오 가치: 2.769931697559578
델타 헷지를 취한 포트폴리오 가치: 5.377939867417446
시나리오 2 (S_new = 52):
델타 헷지 없이 포트폴리오 가치: 9.230279902656218
델타 헷지를 취한 포트폴리오 가치: 17.05430441222985

Γ는 Δ가 기초 자산 가격 S의 변동에 민감하게 반응하는 정도를 측정하는 지표입니다. 수학적으로는:
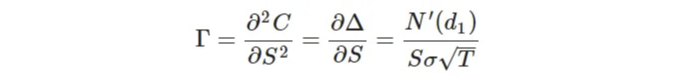
여기서
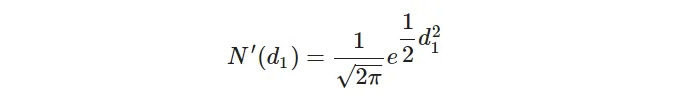
일부 특성:

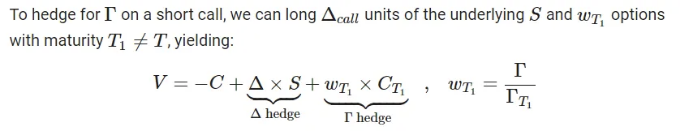
포트폴리오의 전체 감마가 제로가 되도록 가중치 w_'T_1'를 선택합니다 (이를 연습으로 확인할 수 있습니다). 그러나 결과적인 포트폴리오가 델타-중립성을 유지하는 것은 아닐 수도 있습니다. 추가된 요소로 델타 중립성이 해칠 수 있습니다! 다행히도 이를 상대적으로 간단하게 해결할 수 있습니다. 추기하는 방법으로 델타 중립성의 불일치를 다시 조정함으로써.
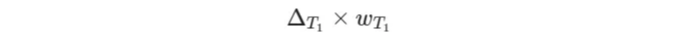
units of the underlying, that is:
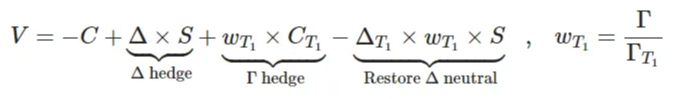
Let’s see a worked out example for illustration:



Just as before, let’s illustrate this with a Python example:
초기 값:
콜 옵션 가격 (C): 2.4004610869656666
델타 (Δ): 0.5216016339715761
감마 (Γ): 0.06554537725247868
헷지용 콜 옵션 가격 (C1): 2.87445202228551
헷지용 감마 (Γ1): 0.05725608663849005
헷지 가중치 (w_T1): 1.1447757103332348
주식 가격 변화: 1
헷지가 없는 포트폴리오 가치: -0.5539863395119156
델타-감마 헷지 적용 후 포트폴리오 가치: -0.0642348870027587
이 예시를 통해 델타와 감마의 변화로 인한 큰 손실을 피하도록 도와준 델타-감마 헷지로 인해 손실을 줄일 수 있음을 확인할 수 있습니다.

세타는 다른 요인들이 일정한 상황에서 만기가 줄어들 때 옵션 가치가 얼마나 줄어드는지를 나타냅니다. 이는 종종 옵션의 "시간 감소"로 불리며 수학적으로 다음과 같이 표현됩니다:
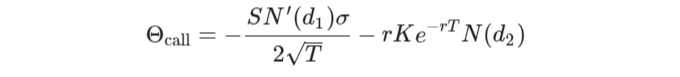
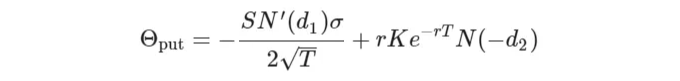
일부 특성:
- 장기 포지션의 경우 세타는 보통 음수입니다. 다른 모든 요인이 일정하다면 시간이 흐름에 따라 옵션의 가치가 감소하기 때문입니다.
- 단기 포지션의 경우 세타는 양수이며, 시간이 지남에 따라 가치가 증가함을 반영합니다.
- 세타는 대체로 ATM(행사가격과 현재 주가가 동일한) 옵션에 대해 높으며, ITM(행사가격보다 주가가 높은) 및 OTM(행사가격보다 주가가 낮은) 옵션에 대해 감소합니다.
- 만기가 다가올수록 ATM 옵션의 경우 세타가 증가하여 시간 가치의 가속화된 감쇠를 반영합니다.
예시를 살펴봅시다. 다음과 같은 매개변수를 갖는 유러피언 콜 옵션이 있다고 가정해봅시다:

이 예는 시간이 중요한 전략인 캘린더 스프레드 또는 시간 퇴조 전략과 같이 Theta가 유용한 정보를 제공하는 방식을 보여줍니다.

이 기사에서 제시된 중요한 그리스 중 마지막으로 소개된 것은 Vega입니다. Vega는 기초 자산의 내재 변동성이 1% 변할 때 옵션 가격이 얼마나 변화하는지를 정량화하여, 다른 모든 요소가 일정하다고 가정합니다. 수학적으로:
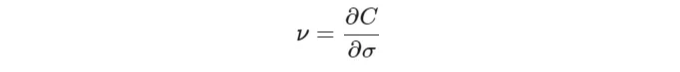
For both call and put options, Vega can be expressed using the Black-Scholes formula as:
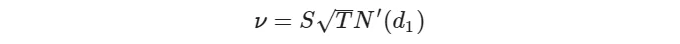
Some characteristics:
- 베가는 항상 양수입니다. 변동성이 증가하면 콜 옵션과 풋 옵션의 가치가 모두 증가합니다.
- 베가는 동일가격에서 가장 높으며, 이후 옵션이 더 많이 더 옵션으로 변화될수록 감소합니다.
- 만기일이 다가감에 따라 베가도 증가하며, 장기적인 옵션에 대한 변동성의 영향이 더 크게 나타납니다.
이와 유사하게, 예시를 살펴봅시다:

콜 옵션의 베가는 대략 6.825이며, 기초 자산의 변동성이 1% 증가한다면 (30%에서 31%로), 모든 조건이 동일한 상태에서 콜 옵션의 가격이 대략 $6.825 증가할 것으로 예상됩니다.
결론
블랙-숄즈 모델은 실제로는 상당히 간단한 근사치이지만, 해당 모델의 연구를 통해 옵션 가격 측정의 여러 동역학과 함의를 수학적으로 이해할 수 있으며, 이러한 것들이 어떻게 유용하고 통찰력 있는 특성들과 관련이 있는지 알 수 있습니다. 이 글에서는 블랙-숄즈 모델에서 가정된 위험 자산의 기초 가격 모델을 다루었으며, 확률적 미적분학과 금융 수학을 사용하여 블랙-숄즈 SDE 및 PDE의 유도를 연구했으며, 가장 중요한 그리스 부분을 다루고 이러한 부분들이 SDE 및 PDE 방정식과 어떻게 관련되는지 살펴보았습니다. 여기서 다루지 않은 많은 내용 (다른 그리스 부분, 내재 변동성 등)이 있지만, 이 글이 해당 모델에 대한 여러 관점을 하나의 글에서 소개할 것이라고 기대합니다.
즐거운 학습되시길 바랍니다!