
지금은 벌써 늦은 밤입니다. 비디오 게임을 즐기고 있고 몇 시간 동안 보석을 모으고 있습니다 🎮 (경험치 또는 아이템을 얻기 위해 동일한 적과 반복적으로 싸우는 것). 갑자기, 당신이 몇 일째 찾고 있던 방어구를 떨어뜨린 적이 나타납니다. 하지만 이미 인벤토리가 꽉 차 있어서 넣을 수가 없습니다. 재배열을 시도해봐도 맞추기 힘듭니다. 이제 무엇을 유지하고 무엇을 버릴지 결정해야 합니다. 다차원 배낭 문제의 흥미로운 세계로 환영합니다. 이 기사에서는 이 문제에 대한 수학적 프로그래밍 모델을 만드는 방법을 보여주고, 파이썬과 Gurobi를 사용하여 문제를 해결하며, 이를 해결하기 위해 적용할 수 있는 일부 휴리스틱 절차를 간단히 논의하겠습니다.
문제와 관련된 수학에 대해 자세히 들어가기 전에, 비디오 게임에서 이 문제가 어떻게 나타나는지와 다른 맥락에서 이를 어떻게 만날 수 있는지에 대해 시간을 할애하고 싶습니다. 오늘날 인벤토리 관리 시스템은 거의 모든 비디오 게임에서 만나볼 수 있습니다. 특히 액션 RPG(역할 재생 게임) 장르인 Diablo 시리즈 및 MMO(대규모 다중 참여 온라인 게임)인 World of Warcraft 또는 Final Fantasy XIV와 같은 게임에서. 이 시스템의 기원은 중세 및 드래곤 게임(Dungeons & Dragons)과 같은 펜 앤지 RPG에 거름될 수 있으며, 이것은 운반 용량 및 부담을 고려한 객체의 무게를 고려했습니다. 그러나 처음으로 이 인벤토리 메커니즘을 통합한 비디오 게임은 1977년 Atari의 클래식 Colossal Cave Adventure였습니다. 그 이후로 많은 비디오 게임이 이 메커니즘의 어떤 버전을 채택했습니다. Pokémon, Dragon Quest, Final Fantasy와 같은 게임은 플레이어가 특정한 수(일반적으로 99)의 항목을 운반할 수 있는 수를 제한한 99 규칙을 적용한 1차원 인벤토리 시스템을 사용했습니다.
게임이 발전함에 따라 이 1차원 시스템은 희소성을 포함하고 게임 경험을 향상시키기 위해 보다 정교해졌습니다. 예를 들어, 저는 현재 Paper Mario: The Thousand-Year Door를 다시 살펴보고 있는데, 아직 간단하고 1차원인데도 더 복잡한 인벤토리 시스템을 갖췄습니다. 이 게임은 플레이어의 인벤토리가 언제든지 15개의 항목을 초과할 수 없도록 하는 규정을 부여했습니다. 플레이어가 무엇을 유지하거나 버릴지를 결정해야 하는 것을 강요하여 모든 항목이 인벤토리에 들어가지 않는다는 사실에 직면하게 합니다. 내게 소모품을 수집하고 세계 곳곳에 흩어진 모든 항목을 모으고 발견하고 싶은 자연스런 수집가로서, 이제 무엇을 유지하거나 버릴지 결정할 때 어떤 기준을 사용해야 하는지 결정해야 합니다. 내 경우엔 항목의 판매 가격을 사용하는 편입니다. Paper Mario에서 해결하려는 문제는 정확히 제한된 항목 수를 초과하지 않고 인벤토리의 총 판매 가격을 최대화하는 것입니다. 이 정확한 문제는 0-1 배낭 문제 또는 1차원 이진 배낭 문제로 알려져 있으며, 다음 섹션에서 공식적으로 설명하겠습니다. 하지만 그 전에, 다른 게임이 보다 정교한 인벤토리 시스템을 개발한 방식을 살펴보겠습니다.
일부 다른 게임, 특히 RPG 판타지 장르의 게임들은 다른 방향을 선택하여 유명한 격자 인벤토리 메카닉 시스템을 구축했습니다. 최초로 이러한 시스템을 시사한 것 중 하나는 The Legend of Zelda (1986)였지만, Baldur's Gate와 Diablo (1997)와 같은 시리즈는 실제로 격자 인벤토리 시스템을 경험의 핵심 부분으로 확립했습니다. 이 시스템에서 플레이어는 고정 크기의 인벤토리 화면을 가지며 각 아이템은 일정한 공간을 필요로 합니다. 이러한 인벤토리 시스템의 예시가 그림 1에 나와 있습니다. 이 메카닉은 플레이어가 인벤토리를 구성하고 아이템의 위치를 최적화하여 독특한 게임 메카닉 경험을 만들 수 있게 합니다. 플레이어는 무엇을 남길지 버릴지 결정하는 것 뿐만 아니라 인벤토리에 아이템을 맞추기 위해 어떻게 배열할지도 결정해야 합니다.
격자 인벤토리 시스템은 많은 유명한 RPG들에서 널리 사용되어 왔지만 놀랍게도, 이 메카닉을 가장 복잡한 형태로 만들어낸 게임은 RPG가 아니라 액션 호러 게임인 Resident Evil 4 (RE4)였습니다. 이 게임에서는 플레이어의 인벤토리가 주인공 레온 S. 케네디의 서류가방으로 제시됩니다. 이전의 격자 인벤토리 시스템과 마찬가지로, 플레이어는 인벤토리 내에서 아이템의 위치를 변경하여 공간을 최적화할 수 있습니다. 그러나 RE4은 플레이어가 아이템을 회전하여 최적의 위치를 달성할 수 있는 추가 자유도를 제공하는 혁신을 도입했습니다. 이 기능을 통해 RE4는 본 게임 안에 "테트리스"와 유사한 미니 게임을 효과적으로 도입했습니다. (그림 2 참조)
이것은 이러한 메커니즘이 구현된 유일한 게임이 아닙니다. 예를 들어, 유명한 어려운 첫인상의 일인칭 슈팅 게임 "타르코프 탈출"도 이 시스템의 변형을 갖추고 있습니다. 게다가, 이 문제의 유사한 버전을 아느 쾌적한 농업 게임에서 찾을 수 있습니다. 스타듀 밸리나 명문화된 문에 같은 문제를 겪습니다. 이 게임에서는 땅을 갖고 있고 그 수익에 따라 심을 작물을 결정해야 합니다. 이어티만 일정량의 시간과 에너지를 소비하는 제약 조건이 있습니다.
더 중요한 것은, 이러한 이차원 배낭 문제에는 비디오 게임 이상의 여러 응용 분야가 있습니다. 물류, 시설 설계, 생산 프로세스 및 기타 다양한 분야 [2-4]에서 이러한 문제를 만납니다. 이 기사의 다음 섹션에서는 학술 논문에서 제시되는 문제를 공식적으로 연구할 것입니다. 수학적 프로그래밍 공식 및 파이썬에서 Gurobi를 사용하여 문제를 해결하는 방법을 살펴볼 것입니다. 마지막으로, 이러한 문제를 해결하는 데 사용할 수 있는 휴리스틱 절차를 간단히 논의할 것입니다.
이제 Gurobi를 사용한 적이 없는 경우, 특히 이 기사에서 사용할 Google Colab(이 기사에서 사용할 IDE)으로부터 Gurobi를 설정하는 방법에 대해 설명한 이전 기사 중 하나를 읽어보시기를 권장합니다. 아래에 기사 링크를 찾을 수 있습니다:
만약 선형 프로그래밍(LP) 또는 정수 프로그래밍(IP) 기술에 대한 자습서와 자세한 정보가 필요하다면, Bruno Scalia C. F. Leite가 작성한 훌륭한 기사를 꼭 확인하시기 바랍니다. 아래에 링크가 있습니다. 또 다른 좋은 소스로는 William의 수학 프로그래밍에 대한 책도 있습니다.
기사 목차:
- 라이브러리 설치 및 Colab 환경 설정
- 0-1 낱개 문제
- 2차원 낱개 문제
- 입력 데이터 및 전처리
- Gurobipy로 문제 해결
- 휴리스틱 접근 방식
- 결론
- 참고 문헌
라이브러리 설치 및 Colab 환경 설정
Google Colab에서 Gurobi를 사용하려면 다음 코드를 사용하여 먼저 설치해야 합니다:
!pip install gurobipy
설치가 완료되면이 프로젝트에 필요한 라이브러리를 가져와서 사용할 수 있습니다.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.patches import Rectangle
from itertools import chain, combinations, permutations, product
import gurobipy as gp
from gurobipy import GRB
from copy import deepcopy
또한 gurobi 세션을 초기화해야 하므로 gurobi 라이센스의 모든 관련 정보를 params 딕셔너리로 만들어야 합니다.
WLSACCESSID = '<여기에 WLSACCESSID를 복사하세요>'
WLSSECRET = '<여기에 WLSSECRET를 복사하세요>'
LICENSEID = '<여기에 LICENSEID를 복사하세요>'
params = {
"WLSACCESSID": WLSACCESSID,
"WLSSECRET": WLSSECRET,
"LICENSEID": LICENSEID,
}
env = gp.Env(params=params) # 이 줄은 gurobi 환경을 초기화합니다.
나머지 가방 문제
나머지 가방 문제는 조합 최적화의 고전적인 문제이며, 더 넓은 절단 및 패킹 (Cutting and Packing, C&P) 문제 클래스의 일부입니다. 나머지 가방 문제에서는 값과 크기가 있는 엔터티 세트가 주어집니다. 목표는 선택된 엔터티들의 값의 합이 최대화되는 동안 크기의 합이 주어진 한계를 초과하지 않도록 한 개 이상의 엔터티를 선택하는 것입니다(가방의 크기). 이것은 Paper Mario에서 설명된 문제와 유사합니다. 비디오 게임에서 바로 적용되는 것 외에도, 나머지 가방 문제는 화물 적재, 프로젝트 선택, 예산 통제, 자본예산편성, 도서관에서 저널 선택 등 산업 환경에서 다양한 응용 분야가 있습니다.
표 태그를 Markdown 형식으로 변경하십시오.
만약 이 섹션을 계속 읽기로 결정했다면, 우리는 내 문제 해결을 통한 Paper Mario: The Thousand-Year Door 인벤토리 문제를 예시로 삼아 진행할 것입니다. 목표는 마리오의 인벤토리 아이템의 판매 가격을 최대화하는 것인데, 전체 15개의 아이템이 필요하다는 것을 고려합니다. 🌶️ Spice things up을 위해, knapsack 형식의 다양성을 보여주기 위해 추가적인 제약 조건을 소개할 것입니다. 마리오의 인벤토리에는 최소한 25의 치유 능력, 적어도 25의 FP 능력, 최소 1개의 상태 복구 아이템, 그리고 적어도 2개의 공격 아이템을 제공하는 조합의 아이템이 포함되어야 합니다. 게다가 각 아이템은 구매 가격이 있으므로, 인벤토리의 총 비용이 200코인을 초과하지 않도록 할 것입니다. 게임에서 동일한 아이템을 여러 번 구매할 수 있기 때문에, 이진 변수 대신 정수 변수를 사용할 것입니다. 문제를 구성하고 해결하는 데 필요한 모든 정보가 아래 표 1에 제시되어 있습니다. 나는 Paper Mario 위키 페이지에서 정보를 추출했습니다. 이 링크에서 CSV 형식의 데이터를 다운로드할 수 있습니다.
이 문제를 gurobipy에서 구성하고 해결하려면, 아래의 코드 스니펫을 따라 하면 됩니다:
paper_mario = pd.read_csv('https://raw.githubusercontent.com/ceche1212/Youtube_optimization/main/paper_mario_items_knapsack.csv')
I = range(len(paper_mario)) # 아이템 I의 세트
model = gp.Model("paper_mario_knp", env=env)
# 변수 생성
x = model.addVars(I, vtype=GRB.INTEGER, name='x')
# 목적 함수
model.setObjective(gp.quicksum(x[i]*paper_mario['판매 가격'][i] for i in I), GRB.MAXIMIZE);
# 제약 조건
model.addConstr(gp.quicksum(x[i] for i in I) == 15) # 15개 미만의 아이템
model.addConstr(gp.quicksum(x[i]*paper_mario['구매 가격'][i] for i in I) <= 200) # 200 이하의 예산
model.addConstr(gp.quicksum(x[i]*paper_mario['치유 능력'][i] for i in I) >= 25) # 최소 25의 치유 능력
model.addConstr(gp.quicksum(x[i]*paper_mario['FP 능력'][i] for i in I) >= 25) # 최소 25의 FP 능력 아이템
model.addConstr(gp.quicksum(x[i]*paper_mario['상태 플레이어'][i] for i in I) >= 1) # 최소 1개의 플레이어 상태 아이템
model.addConstr(gp.quicksum(x[i]*paper_mario['공격'][i] for i in I) >= 3) # 최소 2개의 공격 아이템
# params 설정
tl = 120
mipgap = 0.0
model.setParam('TimeLimit', tl)
model.setParam('MIPGap', mipgap)
# 문제 해결
model.optimize()
모든 것이 계획대로 진행된다면, 총 knapsack 가치는 69가 되어야 하며, 아래 Figure 4와 같은 출력을 볼 수 있어야 합니다.
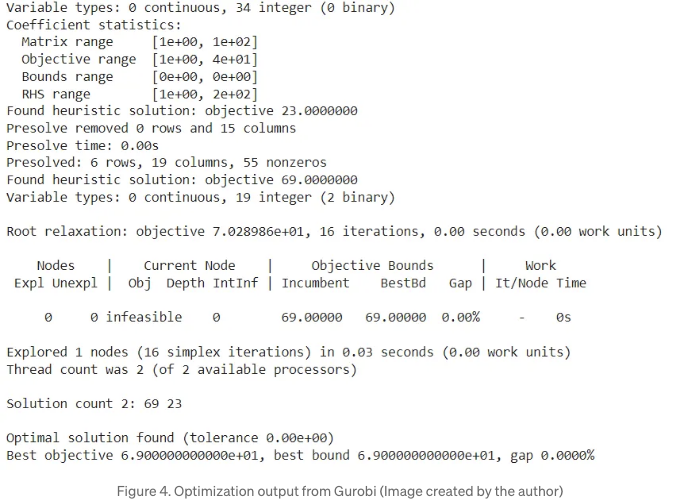
문제를 해결한 후에는 아래 코드 스니펫을 사용하여 솔루션을 쉽게 추출할 수 있습니다:
print("아이템:")
for item in x.keys():
if x[item].x >= 0.99:
print("- ",paper_mario['Item'][item],"QTY:", x[item].x)
print("인벤토리의 총 가치:",model.ObjVal)

2차원 배낭 문제
이제 당신은 배낭 문제의 간단한 버전에 익숙해졌으니, 좀 더 어려운 버전에 도전할 준비가 되었습니다. 물건의 기하학적 형태와 방향을 고려하면, 재고 목록의 각 항목마다 결정해야 할 것이 세 가지로 늘어났습니다: 해당 물건을 인벤토리(배낭)에 넣을지 여부, 포함된 경우 어디에 놓을지, 그리고 사용할 방향(수직 또는 수평) [8]. 간단함을 위해, 모든 항목이 직사각형 또는 정사각형이라고 가정할 것입니다. 그러나 불규칙한 모양을 고려하는 이 문제의 변형도 있다는 점에 유의해야 합니다 [5], 이는 더 복잡한 문제 해결을 필요로 합니다.
이 문제는 비디오 게임 캐릭터의 인벤토리 정리를 넘어서 다양한 응용 분야가 있습니다. 물류 및 운송 분야뿐만 아니라 제품의 생산 및 제조에도 자주 사용됩니다. 형식적으로, 우리의 문제는 주어진 동일한 크기 또는 다른 크기의 직사각형 집합을 선택하고 배치하여, 고정된 크기의 직사각형 내에서 중첩되지 않게, 선택된 항목들의 총 가치를 최대화하는 것으로 정의됩니다. 이전 섹션의 예와 유사하게, 필요시 추가적인 제약 조건을 포함하여 문제를 쉽게 조정할 수 있습니다.
이 문제에는 다음과 같은 변수가 필요합니다:

- 변수 z_i는 재고에 항목 i를 포함할지 여부에 대한 결정에 해당합니다.
- 변수 x_i 및 y_i는 문제의 각 자산을 나타내는 “사각형”의 (x, y) 좌표에 해당합니다. 우리의 문제에는 모든 자산 또는 사각형으로 구성된 I라는 집합이 있습니다.
- 변수 b_i_j_k는 모델에서 "OR" 조건을 설정하는 데 필요한 보조 이진 변수로, 그 사용법은 나중에 자세히 설명됩니다.
- 마지막으로 각 사각형 i는 자산 i가 회전되는지 여부를 결정하는 데 사용될 변수 r_i를 가지게 됩니다.
또한 문제는 다음과 같은 입력 매개변수를 필요로 합니다:

위에서 설명한 변수와 입력 매개변수를 사용하여 문제를 수학적으로 모델링하면 다음과 같은 공식을 사용할 수 있습니다:
The formulation above might look daunting at first sight, but it is actually quite simple. The objective function above is exactly the same as in the “vanilla” 🍦 0–1 Knapsack problem. It is just the sum of the values v_i of the items that are placed inside the inventory (for these items z_i is going to be equal to 1).
Constraint (1) ensures that the the x-coordinate plus the width of each item does not exceeds the Width W of the inventory (considering that the item could be rotated). Similarly, constraint (2) ensures that the the y-coordinate plus the height of each item does not exceeds the Height H of the inventory (considering that the item could be rotated).
위의 공식은 처음 보면 복잡해 보일 수 있지만 실제로는 매우 간단합니다. 위의 목적 함수는 "일반적인" 🍦 0-1 배낭 문제와 정확히 동일합니다. 인벤토리 안에 배치된 항목의 값을 나타내는 v_i의 합일 뿐입니다. (이러한 항목에 대해 z_i가 1이 됩니다.)
제약 조건(1)은 각 항목의 x 좌표 및 너비를 합한 값이 인벤토리의 너비 W를 초과하지 않도록 보장합니다(항목이 회전될 수 있다는 것을 고려합니다). 비슷하게, 제약 조건(2)는 각 항목의 y 좌표와 높이를 합한 값이 인벤토리의 높이 H를 초과하지 않도록 보장합니다(항목이 회전될 수 있다는 것을 고려합니다).
Constraints (3-7)은 서로 다른 항목의 위치 간에 겹침이 없도록 보장합니다. 이러한 제약 조건은 OR 조건으로 작동하며, 변수 b_i_j_1, b_i_j_2, b_i_j_3, 및 b_i_j_4를 각 항목에 사용하고, Big-M 방법을 사용합니다. 요약하면, 한 항목은 다른 항목의 왼쪽, 오른쪽, 위, 또는 아래에 위치할 수 있지만, 겹치지는 않습니다.
Constraints (8-11)은 단순히 변수가 적절한 도메인에 속해 있는지 확인합니다.
입력 데이터 및 전처리
간단히하기 위해, 10개의 항목으로 구성된 다섯 그룹을 사용하겠습니다. 각 그룹 내의 모든 항목은 동일한 차원을 가질 것입니다. 재고는 폭(W)이 15 단위이고 높이(H)가 8 단위인 것으로 합니다. 예제 항목의 차원 및 모든 관련 정보는 아래의 테이블에 표시되어 있습니다.
데이터가 사용 가능하도록 하려면 각 값을 리스트에 저장한 다음 각 항목을 별도의 행으로 준비하는 확장된 데이터프레임을 만들 것입니다. 아래의 코드를 사용하여 이를 구현할 수 있습니다:
widths = [6, 1, 2, 3, 3]
heights = [2, 1, 1, 2, 4]
colors = ['red', 'skyblue', 'green', 'yellow', 'orange']
values = [15, 2, 2, 7, 20]
W = 15
H = 8
quants = [10, 10, 10, 10, 10]
top = max(W, H)
df = pd.DataFrame()
df['quantity'] = quants
df['heights'] = heights
df['widths'] = widths
df['color'] = colors
df['values'] = values
WIDTHS = []
HEIGHTS = []
VALUES = []
COLORS = []
for q, w, h, v, c in zip(quants, widths, heights, values, colors):
for x in range(q):
HEIGHTS.append(w)
WIDTHS.append(h)
VALUES.append(v)
COLORS.append(c)
data_df = pd.DataFrame()
data_df['HEIGHTS'] = HEIGHTS
data_df['WIDTHS'] = WIDTHS
data_df['VALUES'] = VALUES
data_df['COLORS'] = COLORS
N = len(WIDTHS)
M = max(sum(WIDTHS), sum(HEIGHTS))
I = range(N) # 각 자산 "i"의 인덱스를 위해
K = range(4) # OR 변수 "b"의 인덱스를 위해
Gurobipy를 사용하여 문제 해결
이제 필요한 모든 라이브러리와 입력 데이터가 준비되었으므로 Figure 8에 설명된 수학 모델을 만들어볼 차례입니다. GurobiPy를 사용하여 이 모델을 구현하려면 아래의 코드 스니펫을 따라하면 됩니다:
model = gp.Model("두 차원 배낭 문제", env=env)
# 변수 생성
x = model.addVars(I, lb=0, ub=top, vtype=GRB.CONTINUOUS, name="x")
y = model.addVars(I, lb=0, ub=top, vtype=GRB.CONTINUOUS, name="y")
Z = model.addVars(I, vtype=GRB.BINARY, name='Z')
b_vars = [(i, j, k) for i in I for j in I if j != i for k in K]
B = model.addVars(b_vars, vtype=GRB.BINARY, name="B")
R = model.addVars(I, vtype=GRB.BINARY, name='R')
# 목적 함수
model.setObjective(gp.quicksum(Z[i] * data_df['VALUES'][i] for i in I), GRB.MAXIMIZE);
# 제약 조건
for i in I:
model.addConstr(x[i] + (data_df['WIDTHS'][i] * R[i] + data_df['HEIGHTS'][i] * (1 - R[i])) * Z[i] <= W)
model.addConstr(y[i] + (data_df['HEIGHTS'][i] * R[i] + data_df['WIDTHS'][i] * (1 - R[i])) * Z[i] <= H)
for i in I:
for j in I:
if i == j:
continue
else:
model.addConstr(x[i] + (data_df['WIDTHS'][i] * R[i] + data_df['HEIGHTS'][i] * (1 - R[i])) * Z[i] <= x[j] + M * (1 - B[i,j,0]))
model.addConstr(x[j] + (data_df['WIDTHS'][j] * R[j] + data_df['HEIGHTS'][j] * (1 - R[j])) * Z[j] <= x[i] + M * (1 - B[i,j,1]))
model.addConstr(y[i] + (data_df['HEIGHTS'][i] * R[i] + data_df['WIDTHS'][i] * (1 - R[i])) * Z[i] <= y[j] + M * (1 - B[i,j,2]))
model.addConstr(y[j] + (data_df['HEIGHTS'][j] * R[j] + data_df['WIDTHS'][j] * (1 - R[j])) * Z[j] <= y[i] + M * (1 - B[i,j,3]))
model.addConstr(B[i,j,0] + B[i,j,1] + B[i,j,2] + B[i,j,3] >= 1)
주의해야 할 점은 제약조건 (8-11)이 변수 생성 과정에서 이미 설정되었으므로, model.addConstr 메서드를 통해 명시적으로 추가할 필요가 없다는 것입니다. 이제 모델이 완성되었으므로 문제를 해결해 볼 수 있습니다. 이 문제는 복잡하기 때문에 600초(10분) 동안 실행해 보겠습니다. 또한 최적화 과정이 최적값의 5% 이내에 있으면 프로세스를 종료하고 현재까지 얻은 최상의 해를 얻을 수 있도록 설정합니다. 문제를 해결하려면 아래 코드를 따라하세요:
tl = 600
mip_gap = 0.05
model.setParam('TimeLimit', tl)
model.setParam('MIPGap', mip_gap)
model.optimize()
600초 후에 아직 최적해를 확인하지 못했습니다(저희가 모르는 사이에 이미 최적이라고 생각됩니다), 그러나 재고 가치는 상당히 증가했습니다. 초기 값이 35에서 최종 값인 195로 증가했습니다. 이는 원래 값의 거의 6배이며, 꽤 좋은 결과입니다.
문제가 해결되었으니, 솔루션을 추출하고 이를 플롯하는 것만 남았어요. 아래 코드를 따라하면 matplotlib의 Rectangle 객체를 사용하여 쉽게 이를 수행할 수 있습니다:
for item in Z.keys():
if Z[item].x >= 0.99:
print(COLORS[item],Z[item].x,R[item].x >0.5,x[item].x,y[item].x,(WIDTHS[item],HEIGHTS[item]))
아래는 Markdown 표 형식으로 나타낸 print 문의 솔루션 출력을 찾을 수 있습니다:
| Color | Z_i | 회전 | x | y | 크기 |
|---|---|---|---|---|---|
| skyblue | 1.0 | False | 9.0 | 7.0 | (1, 1) |
| skyblue | 1.0 | False | 0.0 | 5.0 | (1, 1) |
| skyblue | 1.0 | False | 14.0 | 7.0 | (1, 1) |
| skyblue | 1.0 | False | 1.0 | 7.0 | (1, 1) |
| skyblue | 1.0 | False | 3.0 | 7.0 | (1, 1) |
| skyblue | 1.0 | False | 10.0 | 7.0 | (1, 1) |
| skyblue | 1.0 | False | 0.0 | 4.0 | (1, 1) |
| skyblue | 1.0 | False | 2.0 | 7.0 | (1, 1) |
| skyblue | 1.0 | False | 8.0 | 7.0 | (1, 1) |
| skyblue | 1.0 | False | 11.0 | 7.0 | (1, 1) |
| green | 1.0 | False | 12.0 | 7.0 | (1, 2) |
| green | 1.0 | False | 4.0 | 7.0 | (1, 2) |
| green | 1.0 | False | 6.0 | 7.0 | (1, 2) |
| green | 1.0 | True | 0.0 | 6.0 | (1, 2) |
| yellow | 1.0 | True | 9.0 | 4.0 | (2, 3) |
| orange | 1.0 | False | 3.0 | 0.0 | (4, 3) |
| orange | 1.0 | False | 12.0 | 0.0 | (4, 3) |
| orange | 1.0 | True | 1.0 | 4.0 | (4, 3) |
| orange | 1.0 | False | 9.0 | 0.0 | (4, 3) |
| orange | 1.0 | True | 5.0 | 4.0 | (4, 3) |
| orange | 1.0 | False | 6.0 | 0.0 | (4, 3) |
| orange | 1.0 | False | 0.0 | 0.0 | (4, 3) |
| orange | 1.0 | True | 11.0 | 4.0 | (4, 3) |
저희 인벤토리에는 빨간색 항목이 선택되지 않았는지 확인할 수 있습니다. 공간이 소비되었으나 포함하지 않을 가치가 충분하지 않아 보입니다. 아래 표 10을 확인하여 최종 인벤토리의 시각적 표현을 확인할 수도 있습니다.
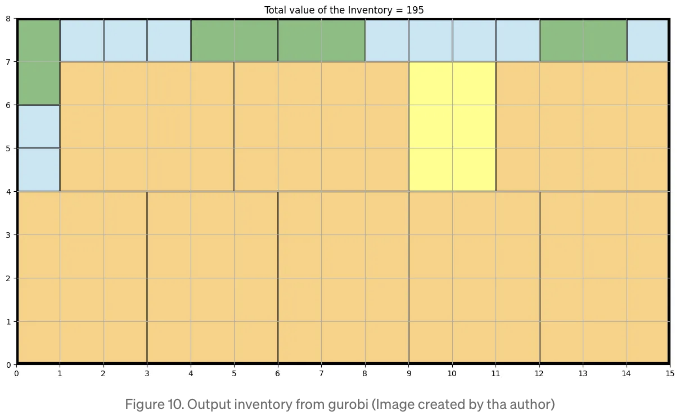
휴리스틱 접근법
문제에서 언급했듯이 이 문제는 건설적 휴리스틱을 사용하여 문헌에서 다루어졌습니다. 왜 휴리스틱이 사용되는지 궁금할 수 있습니다. 답은 간단합니다. 휴리스틱은 빠르고 계산 비용이 적습니다. 휴리스틱은 최적성을 보장하지는 않지만 품질 측면에서 놀랍도록 좋은 해결책을 빠르고 비용 효율적으로 제공합니다.
다행히도, 이 문제를 해결하기 위해 특별히 설계된 Python 라이브러리인 rectpack이라는 라이브러리가 있습니다. 이 라이브러리는 재고의 항목 배열만 다루며 문제의 가치 최대화 부분을 직접 해결하지는 않습니다. 그러나 라이브러리에서 제공하는 여러 알고리즘을 시도함으로써 어떤 것이 최상의 재고 가치를 제공하는지 확인할 수 있습니다. 이 라이브러리 사용에 대한 자세한 내용은 Samir Saci가 쓴 훌륭한 Medium 게시물을 추천합니다.
결론
마지막으로, 이 기사는 수학적 프로그래밍을 사용하여 2차원 낙석 문제를 해결하는 과정을 안내해드렸습니다. 우리는 기본 0-1 낙석 문제와 그것을 Gurobi에서 구현하는 방법으로부터 시작했습니다. 그런 다음, 우리는 문제의 2차원 버전을 위한 혼합 정수 선형 프로그래밍(MILP) 공식과 그 문제를 Gurobi를 사용하여 어떻게 해결할지 탐구했습니다. 마지막으로, 건설적 휴리스틱과 rectpack 라이브러리를 간단히 논의했습니다. 이 기사를 즐겨주셨고 실생활 맥락에서 비슷한 변형의 문제에 대해 더 알고 싶다면, 이전에 게시한 2차원 조합 문제에 관한 기사를 확인하시기를 권장합니다. 기사 링크는 아래에 제공되어 있습니다.
제 RE4 인벤토리를 최적화하거나 스타듀 밸리의 농장 플롯을 개선하려는 누구에게든 도움이 되는 리소스로 써드루 밸리의 코드 개발을 포함한 이 기사가 도움이 되었으면 좋겠어요 😂. 이 기사에 대한 완전한 노트북은 아래 GitHub 저장소 링크에 있습니다.
정말로 이 기사가 유용하고 재미있었기를 바라며, 만약 그렇다면 귀하의 생각을 듣고 싶습니다! 의견을 남기거나 👏 클랩으로 감사를 표현해주시면 감사하겠습니다. 그리고 제 최신 기사를 업데이트하고 싶다면, Medium에서 저를 팔로우해보세요. 귀하의 지지와 피드백이 저에게 더 탐구하고 이 매력적인 분야를 공유하도록 동기를 부여합니다. 읽어주셔서 감사하며, 다음 기사에서 더 많은 통찰력을 기대해주세요!
참고 자료
- [1] Williams HP. Model Building in Mathematical Programming. 4판. Chichester: Wiley; 1999
- [2] Caprara, A. 및 Monaci, M., 2004. On the two-dimensional knapsack problem. Operations Research Letters, 32(1), pp.5–14.
- [3] Baker, B.S.; Coffman Jr, E.G.; Rivest, R.L. (1980) Orthogonal packings in two dimensions. SIAM Journal of Computing 9(4): 846–855.
- [4] Del Valle, A.M.; Queiroz, T.A.; Miyazawa, F.K.; Xavier, E.C. (2012) Heuristics for two-dimensional knapsack and cutting stock problems with items of irregular shape. Expert Systems with Applications 39(16): 12589–12598.
- [5] DellaFave, R. (2014) Designing an RPG Inventory System That Fits: https://gamedevelopment.tutsplus.com/designing-an-rpg-inventory-system-that-fits-preliminary-steps--gamedev-14725a
- [6] Martello, S. & Toth, P. (1990) Knapsack Problems: Algorithms and computer implementations. John Wiley & Sons, West Sussex.
- [7] Salkin, H.M. & de Kluyver, C.A. (1975) The Knapsack Problem: a survey. Naval Research Logistics Quarterly 22(1): 127–144.
- [8] Bortfeldt, A. & Winter, T. (2009) A genetic algorithm for the Two-dimensional Knapsack Problem with rectangular pieces. International Transactions in Operational Research 16: 685–713.