요약
배경: 열 확산은 다양한 과학 및 공학 분야에서 근본적인 문제로, 효율적인 계산 모델링 기술이 필요합니다. 셀룰러 오토마타에서 유래된 폰 노이만 이웃은 격자 기반 시스템에서 이러한 과정을 시뮬레이션하는 간단한 프레임워크를 제공합니다.
문제: 열 확산을 정확하게 모델링하려면 계산 상 간단함과 이산 셀 간 열 전달의 본질적인 역학을 포착할 수 있는 방법이 필요합니다.
접근 방식: 본 글에서는 폰 노이만 이웃을 적용하여 이차원 그리드에서 열 확산을 시뮬레이션하는 방법을 탐구합니다. 이산적인 열 방정식을 사용하여 각 셀의 온도를 업데이트하며, 이웃한 네 방향 (북, 남, 동, 서)의 온도에 기초하여 이루어집니다.
결과: 이 시뮬레이션은 중앙 열원으로부터 열이 균일하고 대칭적으로 확산되는 패턴을 명확하게 나타내며, 온도 그래디언트를 적확하게 보여주는 컬러 코딩된 히트맵을 통해 정확하게 표현하고 있습니다. 폰 노이만 이웃은 열의 주요 방향성 흐름을 효과적으로 모델링하며, 이산형 계산 시스템에서의 유틸리티를 입증합니다.
결론: 폰 노이만 이웃은 격자 기반 모델에서 열 확산을 시뮬레이션하는 견고하고 효율적인 방법을 제공합니다. 그 간단함과 효과적인 성능은 엔지니어와 과학자들에게 유용한 도구로, 다양한 실용적인 응용 프로그램에서 열 전달 역학의 정확한 표현을 가능하게 합니다.
키워드: 열 확산; 폰 노이만 이웃; 세포자동기; 계산 모델링; 이산형 열 방정식.
소개
컴퓨터 모델링에서 일부 개념이 열 확산만큼 광범위하게 적용되는 것은 없습니다. 열 확산은 재료의 열 속성을 최적화하려는 엔지니어이든 기후 패턴을 모델링하는 과학자이든 상관없이, 서로 다른 매체를 통해 열이 이동하는 방식을 이해하는 것이 중요합니다. 그렇다면 이 복잡한 물리적 과정을 컴퓨터 모델로 어떻게 전환할까요? 답은 세포 자동자에서 기본 개념인 폰 노이만 이웃[von Neumann neighborhood]에 있습니다.
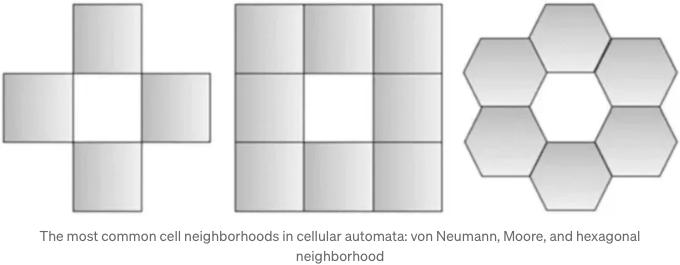
폰 노이만 이웃: 세포 자동자의 중추 개념
각각이 재료의 이산적 부분을 나타내는 셀 그리드를 상상해보세요. 각 셀의 온도는 시간이 지남에 따라 변화하며, 주변 셀의 온도에 영향을 받습니다. 이것이 폰 노이만 이웃이 중요한 이유입니다. 천재 수학자 존 폰 노이만에 의해 명명된 이 이웃은 어떤 셀에 대해 직접 인접한 네 개의 셀을 포함합니다: 북, 남, 동, 서. 이는 그리드 기반 시스템에서 상호 작용을 모델링하는 간단하면서도 강력한 방법입니다.
열 확산: 기본 개념
열 확산은 열이 높은 온도에서 낮은 온도 영역으로 퍼지는 방식을 설명합니다. 연속적인 매체에서는 열 방정식이 이 과정을 지배하는 편미분 방정식입니다. 그러나 우리 그리드와 같은 이산 시스템에서는 다른 접근 방식이 필요합니다. 여기서는 폰 노이만 이웃의 온도에 기초하여 각 셀의 온도를 업데이트하는 이산 열 방정식을 사용합니다.
이론에서 실무로: 열 확산 구현하기
폰 노이만 이웃을 사용하여 열 확산을 실제로 구현하는 방법에 대해 살펴봅시다. 각 셀이 물질의 작은 부분을 나타내는 2차원 그리드를 고려해보세요. 각 셀의 온도는 다음 규칙에 따라 이산 시간 단계에 걸쳐 진화합니다:
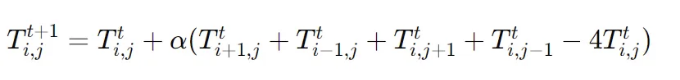
여기서 T_(i,j)t은 시각 t에서 (i,j) 위치의 셀 온도를 나타내고, α는 열 확산 상수입니다. 이 방정식은 열 확산의 본질을 포착합니다: 셀의 온도는 주변 셀이 더 뜨거우면 증가하고, 주변 셀이 더 차가우면 감소합니다.
실용적 응용 및 그 이상
폰 노이만 이웃과 함께 열 확산을 모델링하는 것은 학계에서만 하는 연습이 아닙니다. 이는 재료과학부터 환경 모델링까지 다양한 분야에서 실제 응용이 있습니다. 엔지니어들은 새로운 소재의 열적 특성을 최적화하기 위해 사용할 수 있으며, 과학자들은 지구 대기나 해양에서 열 흐름을 모델링할 수 있습니다. 또한 이 방법은 유체 역학이나 화학 확산과 같이 더 복잡한 현상으로 확장할 수도 있습니다.
단계별 시뮬레이션
이 모델을 구현하는 간단한 Python 스크립트를 사용할 수 있습니다. 가운데 열원을 제외하고 모든 곳의 온도가 0인 그리드로 시작합니다. 시간이 지남에 따라 열이 그리드를 통해 어떻게 퍼지는지 관찰하게 됩니다.
import numpy as np
import matplotlib.pyplot as plt
# 매개변수
alpha = 0.1 # 열 확산율
그리드 크기 = 50
시간 단계 = 100
# 초기 온도 분포가 있는 그리드로 초기화
그리드 = np.zeros((그리드 크기, 그리드 크기))
그리드[그리드 크기//2, 그리드 크기//2] = 100 # 초기 열원
# 폰 노이만 이웃에 기반한 그리드를 업데이트하는 함수
def update_grid(grid, alpha):
new_grid = grid.copy()
for i in range(1, 그리드 크기-1):
for j in range(1, 그리드 크기-1):
new_grid[i, j] = grid[i, j] + alpha * (
grid[i+1, j] + grid[i-1, j] + grid[i, j+1] + grid[i, j-1] - 4*grid[i, j])
return new_grid
# 시뮬레이션
for _ in range(시간 단계):
그리드 = update_grid(그리드, alpha)
# 시각화
plt.imshow(그리드, cmap='hot', interpolation='nearest')
plt.colorbar()
plt.title('폰 노이만 이웃을 사용한 열 확산')
plt.show()
이 스크립트는 가운데 열원이 있는 그리드를 초기화하고 100개의 시간 단계 동안 열 확산 시뮬레이션을 수행합니다. update_grid 함수는 폰 노이만 이웃에 기반하여 각 셀의 온도를 업데이트하는 이산 열 방정식을 적용합니다. 최종 온도 분포는 히트맵을 사용하여 시각화되며, 열이 그리드를 통해 어떻게 퍼지는지 보여줍니다.
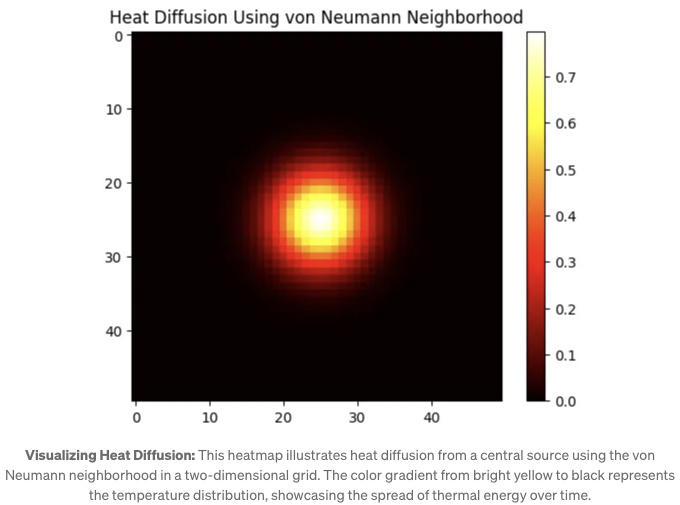
해당 이미지는 폰 노이만 이웃을 사용하여 2차원 그리드에서 열 확산 시뮬레이션 결과를 보여주는 히트맵입니다. 이 히트맵의 해석은 다음과 같습니다:
색상 그라디언트:
- 색상 그라디언트는 검은색(낮은 온도를 나타냄)에서 밝은 노란색/흰색(높은 온도를 나타냄)까지 범위가 있습니다.
- 열원으로 시작한 중앙 영역이 가장 밝은 색으로, 가장 높은 온도를 나타냅니다.
- 중심으로부터 멀어질수록 색상이 빨간색과 주황색에서 검은색으로 변하며, 온도가 점진적으로 감소함을 보여줍니다.
열 확산 패턴:
- 이 패턴은 대칭적이고 원형이며, 중심점에서 시작되는 확산 과정에 특징적입니다.
- 폰 노이만 이웃은 열이 주로 북쪽, 남쪽, 동쪽 및 서쪽으로 퍼진 후 다른 셀로 확산되도록 보장합니다.
온도 척도:
- 오른쪽에 있는 컬러 바는 색에 해당하는 온도 값을 나타냅니다.
- 중앙 영역의 가장 높은 온도는 0.7에 가깝지만, 외부 영역은 0에 가까워집니다.
격자 크기 및 경계:
- 격자는 50x50 행렬이며, 축 레이블은 0에서 49까지의 범위입니다.
- 열원은 중앙에 위치하기 때문에 열이 범위 내에서 충분히 퍼지지 않았기 때문에 격자의 경계는 최저 온도로 유지됩니다.
시뮬레이션 시간 단계:
- 부드러운 그라데이션은 열이 균등하게 확산되도록 여러 번 반복된 것을 시사합니다.
- 시뮬레이션은 아마도 충분한 시간 단계를 거쳐 이 확산 단계에 도달할 수 있을 만큼 충분히 실행되었을 것으로 보입니다.
이 히트맵은 폰 노이만 이웃을 사용하여 중앙 출처에서 열이 시간이 지남에 따라 어떻게 확산되는지 명확하게 시각화합니다. 이는 방사 대칭과 효과적인 열 확산을 강조하며 이산 열 방정식에 의해 모델링됩니다.
결론
요약하면, 폰 노이만 이웃은 이산 시스템에서 열 확산을 시뮬레이션하는 간단하면서도 강력한 프레임워크를 제공합니다. 복잡한 열 전달 과정을 간단한 지역 상호 작용으로 분해함으로써, 우리는 다양한 실용적 응용 프로그램을 가진 정확하고 효율적인 모델을 생성할 수 있습니다. 엔지니어, 과학자, 교육자이든, 이 접근 방식을 이해하고 구현하는 것은 여러분의 작업에서 새로운 가능성을 열 수 있습니다.
폰 노이만 이웃의 원칙이 다른 유형의 확산 과정이나 계산 모델에 어떻게 적용될 수 있을까요? 아래 댓글에서 여러분의 생각과 경험을 공유해주세요!