이 게시물은 Rafael Guedes와 함께 작성되었습니다.
소개
시계열 기초 모델의 개발이 지난 두 분기 동안 가속화되고 있으며 매달 새로운 모델이 출시되고 있는 것을 목격하고 있습니다. 2023년 마지막 분기에 TimeGPT [1]가 출시되었으며 그 이후로 Lag-Llama [2], 구글의 TimesFM [3], 아마존의 Chronos [4], Salesforce의 Moirai [5] 등이 출시되었습니다.
기초 모델에 대한 증가하는 관심을 이해하기 위해 핵심 능력인 제로샷 추론을 정의해야 합니다. 이는 이러한 모델이 훈련 단계에서 만나보지 못한 데이터에서 작업을 정확하게 수행하거나 예측하는 능력을 가리킵니다. 이 능력은 자연어 처리(NLP), 컴퓨터 비전, 텍스트와 이미지를 결합하는 다중 모달 작업 등 다양한 영역에 적용된 모델에서 탐구되었습니다. "제로샷"이라는 용어는 모델이 특정 작업이나 데이터 도메인에서 훈련 중에 "제로" 예제를 보지만 그 영역에서 효과적으로 작업을 수행하려하는 능력에서 나왔습니다. 이 용어는 2009년 Hinton 등에 의해 저술된 "시맨틱 출력 코드를 사용한 제로샷 학습" 논문에서 소개되었으며 같은 해 NIPS 컨퍼런스에서 발표되었습니다. 그 이후로 가장 중요한 연구 주제 중 하나로 등장하여 이제는 시계열 분석 분야로 진입하고 있습니다.
이 기사에서는 Salesforce가 제공하는 Moirai라는 새로운 시계열 예측을 위한 기반 모델을 탐구합니다. 이는 시계열 예측을 위한 기반 모델에 대한 시리즈 기사들을 기반으로 하며, TimeGPT 및 Chronos와 같은 모델의 성능을 실제 데이터셋에서 자세히 설명하고 보여준 기사들을 바탕으로 합니다.
Moirai 뒤의 아키텍처와 제로샷 추론을 가능하게 하는 주요 구성 요소에 대한 심층적인 설명을 제공합니다. 우리는 또한 지금까지 조사한 Moirai와 다른 두 기반 모델 간의 차이점을 요약합니다. 예를 들어, 훈련 데이터의 크기, 모델 매개변수 수, 그리고 다변량 예측을 허용하는지 여부를 비교합니다.
이론적 개요를 마친 후에는 Moirai를 특정 사용 사례와 데이터셋에 적용합니다. 우리는 구체적인 실행 세부 사항을 다루고 모델의 성능을 철저히 분석합니다. 마지막으로, Moirai의 성능을 TiDE와 Chronos와 공개 데이터셋을 사용하여 비교합니다.

항상 코드는 GitHub에서 확인하실 수 있습니다.
배경
시계열 예측에서 주요 개념을 정의하여 Moirai가 다루는 시계열 문제를 이해하기 쉽도록 설명합니다.
단일 변수 시계열 예측은 과거 값만을 사용하여 단일 시계열 변수의 미래 값을 예측하는 것에 초점을 맞춥니다. 예측 모델은 단일 변수의 과거 데이터를 활용하여 미래 예측을 위한 패턴, 추세 및 주기를 식별합니다. 예를 들어, 과거 온도 기록만을 기반으로 내일의 온도를 예측하는 것이 있습니다.
다변량 시계열 예측은 과거 데이터를 기반으로 관련된 여러 시계열 변수의 미래 값을 예측하는 것을 의미합니다. 이 맥락에서 예측 모델은 여러 변수 간의 상호의존성과 상호작용을 고려하여 예측을 수행합니다. 예를 들어 제품의 미래 판매량을 예측할 때, 과거 판매뿐만 아니라 마케팅 비용, 계절적 추세, 경쟁사 가격과 같은 관련 요인도 고려될 수 있습니다.
시계열 예측에서의 공변량은 예측 결과에 영향을 미칠 수 있는 변수를 말합니다. 이러한 변수들은 사전에 알려진 것이거나 예측 기간 동안 추정될 수 있습니다. 단변량 및 다변량 예측 모델에서 공변량은 대상 변수의 과거 데이터를 넘어 추가적인 통찰을 도입합니다. 예를 들어 공휴일, 특별 이벤트, 경제 지표와 같은 요소들이 있습니다. 더불어 다변량 예측에서는 공변량이 관련 시계열 데이터로 확장될 수 있는데, 이는 미래 값이 알려진 변수들이거나 예측이 필요한 변수들을 설명합니다.
시계열 빈도는 시계열 데이터 점들이 기록되거나 관찰되는 간격을 나타내며, 시간에 따른 데이터의 규칙성과 세분화를 대표합니다. 이 빈도는 금융 시장의 분 단위 거래와 같이 높은 주파수 데이터부터 연간 경제 지표와 같은 저주파수 데이터까지 다양할 수 있습니다. 또한 다른 빈도는 다양한 추세, 패턴 및 계절성을 포착할 수 있습니다. 예를 들어 일일 판매 데이터는 월별 집계에서 보이지 않는 주간 주기나 특정 요일의 영향과 같은 패턴을 드러낼 수 있습니다.
확률적 예측은 가능한 미래 결과의 분포를 제공하여 점 예측을 넘어 확장합니다. 이 출력 분포는 다양한 미래 값이 발생할 확률을 나타내며, 불확실성 하에서 더 통찰력 있는 의사결정을 가능케 합니다. 예를 들어 판매량이나 에너지 소비와 같이 관측 값이 엄격히 양수인 경우, 확률적 예측은 가능한 결과 값 범위를 모델링하기 위해 로그-정규분포나 감마 분포를 활용할 수 있습니다. 확률적 예측은 위험 관리와 계획에 특히 유용하며, 가장 비관적적부터 가장 낙관적인 시나리오까지 다양한 상황의 발생 가능성을 이해할 수 있도록 합니다.
Moirai: Salesforce의 시계열 기반 모델
모이라이(Moirai)는 Salesforce에서 개발한 시계열 예측을 위한 기본 모델입니다. 이 모델은 다양한 시계열을 예측할 수 있는 범용 모델로서 설계되었습니다. 이 유연성을 달성하기 위해 해당 모델은 시계열 데이터와 관련된 여러 가지 문제를 다룹니다. 예를 들어, 다음과 같은 능력을 갖추고 있습니다:
- 모든 종류의 데이터 주파수(시간당, 일일, 주간 등) 다루기;
- 미래에 알려지지 않은 경우에도 어떠한 종류의 공변수도 수용하기;
- 유연한 분포를 사용하여 여러 상황에 적응할 수 있는 확률적 예측 생성.
데이터셋은 기초 모델의 주요 구성 요소 중 하나입니다. 저자들은 9개의 다양한 시계열 도메인에 걸쳐 270억 건의 관측치로 이루어진 대규모이자 다양한 데이터셋을 구축했습니다. (예시 활용, 다양성, 확신 정도) 게다가, 저자들은 세 가지 주요 혁신적 개념을 도입했습니다: Multi Patch Size Projection Layers(다중 패치 크기 투영 레이어), Any-Variate Attention(모든 공변수 관심), 그리고 Mixture Distribution(혼합 분포)각각에 대해 다음 섹션에서 자세히 설명합니다.
Multi Patch Size Projection Layers
시계열에 패치 개념이 처음 소개된 것은 PatchTST [7]였습니다. 이것의 목표는 시계열 데이터를 크기 P의 패치로 나누는 것이었습니다. 즉, 이는 원래 시리즈의 짧은 하위 집합인 패치로 나누는 것이죠. 그렇다면 시계열 예측의 기본 모델에서 패치를 사용하는 것이 왜 유용한 걸까요?
시계열 예측은 각 다른 시간 단계의 데이터 간 상관 관계를 이해하려는 목표를 가지고 있습니다. 기본 모델은 주로 트랜스포머(Transformer) 기반의 아키텍처를 사용합니다. NLP 애플리케이션에는 트랜스포머가 잘 작동하지만, 시간 단계 하나는 문장의 단어처럼 의미가 없습니다. 그래서 우리는 주의 메커니즘을 적용하기 위해 지역 의미 정보를 추출할 방법이 필요합니다. 시리즈를 패치로 나누면 시간 단계를 리치한 의미 표현을 가진 서브시리즈 수준 구성 요소로 종합할 수 있습니다.
더 간단히 말하면, 단어 임베딩이 단어를 고차원 공간에서 표현하는 것처럼, 시계열 패치는 그들의 특징에 의해 정의된 다차원 공간에서 시리즈 세그먼트의 표현으로 간주할 수 있습니다.
이 프로세스는 여러 이점을 제공합니다:
- 싱글 타임 스텝이 아닌 시계열 그룹을 살펴 지역적 의미를 추출하기 위한 주의 메커니즘 활성화;
- 인코더에 공급되는 토큰 수를 줄이고, 이에 따라 필요한 메모리를 줄여 모델에 더 긴 입력 시퀀스를 공급할 수 있는 것;
- 더 긴 시퀀스로 인해 모델은 처리해야 할 정보가 더 많아지고 의미 있는 시간적 관계를 추출할 수 있어 더 정확한 예측을 할 수 있습니다.
저자들이 사용하는 패치 크기는 데이터 빈도에 따라 다르며, 저주파수 데이터일수록 작은 패치 크기를 갖고 고주파수 데이터일수록 큰 패치 크기를 갖습니다:
- 연간 및 분기별 → 패치 크기 8
- 월간 → 패치 크기 8, 16, 32
- 주간 및 일일 → 패치 크기 16, 32
- 시간 단위 → 패치 크기 32, 64
- 분 단위 → 패치 크기 32, 64, 128
- 초 단위 → 패치 크기 64, 128
모델 아키텍처에 대해 저자들은 입력 및 출력 패치 레이어를 사용했습니다. 데이터를 패치로 변환한 후, 입력 패치 레이어인 간단한 선형 레이어가 시계열 서브셋을 패치 임베딩으로 매핑하여 엔코더 전용 트랜스포머 레이어로 전달합니다. 나중에 두 번째 패치 레이어가 사용되어 엔코더의 출력을 처리합니다. 출력 토큰은 다중 패치 크기 출력 프로젝션을 통해 디코딩됩니다. 다섯 가지 다른 패치 크기가 있기 때문에 모델은 입력 데이터를 처리하는 데 사용된 패치 크기에 따라 활성화되는 다섯 가지 다른 입력 패치 레이어와 다섯 가지 다른 출력 패치 레이어가 있습니다.
더 명확히 설명하기 위해 특정 예시를 살펴보겠습니다. 분기별 시계열을 예측하고자 한다고 가정해봅시다. 데이터는 크기가 8인 P개의 패치로 세분화됩니다. 이러한 패치는 이후 8 크기의 패치에 대해 설계된 입력 패치 레이어에 의해 처리됩니다. 이 레이어에서 생성된 패치 임베딩은 엔코더 전용 트랜스포머로 전달되어 임베딩을 처리합니다. 마지막으로, 처리된 임베딩은 다시 8 크기의 패치 레이어를 통해 출력됩니다.
다변량 어텐션
전통적인 Transformer 아키텍처는 단일 시퀀스의 대상 값만 받아 들이도록 설계되어 있습니다. 그러나 이 모델은 다변량 시계열 시나리오에서 여러 시퀀스의 대상 값 및 동적 공변량을 다루기를 기대합니다. 따라서 저자들은 Moirai가 여러 시퀀스를 처리할 수 있도록 "Any-Variate Attention"을 도입했습니다.
이 프로세스는 여러 시계열(변수)을 값의 단일 시퀀스로 평평하게 만드는 것으로 시작합니다. 그런 다음, 모델이 주의 점수를 계산할 때 중요한 서로 다른 변수들을 구별할 수 있도록 변수 인코딩이 적용됩니다.
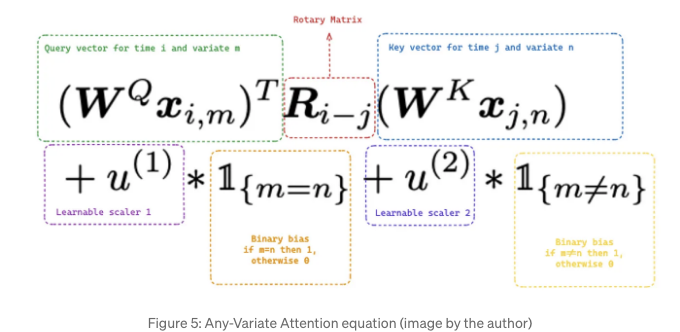
"Any-Variate Attention"에는 두 가지 기본 특성이 있습니다: 변수 순서에 대한 순열 등변성과 변수 지수에 대한 순열 무변성을 달성합니다.
Permutation Equivariance in relation to variate ordering means that if the observation sequence within a variate is rearranged, the model's output for that variate will reflect the same rearrangement. This property is essential as we are dealing with time series data, and the chronological order must be maintained within each variate. As a result, the model's comprehension of time series dynamics remains consistent regardless of the input sequence.
Permutation Invariance concerning variate indices implies that the model's output remains unchanged even if the variates are reordered. For example, suppose we are processing temperature and humidity data as two variates in a multivariate time series framework. If we choose to change the sequence in which these variates are fed into the model (e.g., presenting humidity first and then temperature instead of temperature first and then humidity), it should not impact the final result. The model treats variate indices as interchangeable, focusing on the encoded relationships instead.
To achieve permutation equivariance/invariance, Moirai employs two different techniques:
- Rotary Positional Embeddings (RoPE) [8] enforce permutation equivariance through their encoding mechanism. They represent positional information by rotating tokens in the embedding space based on their positions in the sequence. This allows the model to retain the absolute positions of tokens while preserving the relative distances between any pair of tokens.
- Binary attention bias helps the model achieve invariance by treating variates as if they are not ordered. The model dynamically adjusts its focus by applying various attention biases (learnable scalars) depending on whether elements belong to the same variate (m=n) or different variates (m≠n). This empowers the Any-variate Attention mechanism to accommodate diverse numbers of variates and their permutations.
혼합 분포
Moirai는 확률적 예측 모델로, 단순히 하나의 점 예측을 제공하는 대신 분포의 매개변수를 학습합니다. 분포로 출력되는 결과는 예측의 불확실성을 결정자가 낮은 간격은 모델의 예측에서 큰 불확실성을 나타냅니다.
DeepAR과 같은 다른 확률 모델들처럼, Moirai의 목적은 손실 함수, 특히 음의 로그-우도를 최소화하여 확률 분포의 매개변수를 추정하는 것입니다. 최적화를 위해 여러 가능한 분포가 있습니다. 예를 들어, DeepAR은 가우시안, 베타, 음이항 또는 스튜던트 t-분포의 매개변수를 추정하도록 구성할 수 있습니다.
Moirai는 토대 모델이기 때문에 다양한 데이터 도메인을 예측할 수 있도록 설계되었으며, 따라서 단일 분포로 제한될 수 없습니다. 가능한 모든 시나리오를 수용하기 위해 모델은 다양한 종류의 데이터에 적합한 혼합 분포의 매개변수를 학습합니다:
- Student의 t-분포는 꼬리가 무거운 데이터나 이상치를 처리할 수 있는 능력으로 대부분의 시계열 데이터에 대해 견고한 옵션입니다.
- 음이항 분포는 음수 값을 예측하지 않기 때문에 엄격히 양의 카운트 데이터에 유용합니다.
- 로그-정규 분포는 경제 지표나 자연 현상과 같이 오른쪽으로 치우친 데이터를 효과적으로 예측합니다.
- 낮은 분산 정규 분포는 평균 주변에 군집된 데이터에 사용되며, 높은 신뢰도의 예측에 적합합니다.
TimeGPT 대 Chronos 대 Moirai: 비교
이 섹션은 이전 글들에서 다룬 토대 모델들 간의 유사점과 차이점을 제시합니다.

테이블 1은 기초 모델들의 주요 특성을 비교합니다. 이 단계에서는 성능을 비교하는 데 초점을 맞추지 않았으며, 그 내용은 다음 섹션에서 다룰 것입니다. 우리는 Chronos와 Moirai가 오픈 소스 모델이며 커뮤니티 기여를 통해 발전할 것이라고 이야기해드려야 합니다. 그러므로, 결정을 내리는 데 의구심이 든다면 오픈 소스 모델을 선택하고, 시간이 지남에 따라 개선되는 잠재력과 커뮤니티 지원이 큰 모델로 가는 것을 권장합니다. 중요한 결론은 Chronos가 훨씬 더 효율적인 데이터를 보여주는데, 훈련 데이터가 훨씬 적게 필요하다는 점입니다. 그러나, 이 모델은 아직 다변량적이지는 않습니다. 마지막으로, 매개 변수의 수를 살펴보면 시계열 모델이 LLMs보다 상당히 더 작아서 사용자 친화적이며 배포하기가 더 쉽다는 것을 알 수 있습니다.
Moirai vs. Chronos: 공개 데이터셋에서의 비교
이 섹션에서는 Moirai를 사용하여 실제로 공개적으로 이용 가능한 cc-by-4.0 라이선스하에 있는 호주 관광객을 예측할 것입니다. 이후에 Moirai의 예측 성능을 Chronos (큰 버전) 및 TiDE와 비교할 것입니다 (Chronos 및 TiDE로 생성된 예측 코드를 얻으려면, 저희의 마지막 기사를 확인해주세요).
경제 변수(CPI, 인플레이션율, GDP 등)를 Trading Economics에서 추출한 것으로 강화된 데이터셋을 소개합니다. Trading Economics는 공식 소스를 기반으로 한 경제 지표를 사용합니다. 데이터셋의 사용성을 높이기 위해 전처리 작업을 수행했습니다. 우리는 전처리된 데이터셋 버전을 저장하여 실험을 쉽게 재현할 수 있도록 했습니다.
먼저 라이브러리를 가져와 전역 변수를 설정합니다. 날짜 열, 대상 열, 동적 변수, 시리즈 빈도 및 예측 기간을 설정합니다.
%load_ext autoreload
%autoreload 2
import torch
import pandas as pd
import numpy as np
import utils
from datasets import load_dataset
from gluonts.dataset.pandas import PandasDataset
from huggingface_hub import hf_hub_download
from uni2ts.model.moirai import MoiraiForecast
TIME_COL = "Date"
TARGET = "visits"
DYNAMIC_COV = ['CPI', 'Inflation_Rate', 'GDP']
SEAS_COV=['month_1', 'month_2', 'month_3', 'month_4', 'month_5', 'month_6', 'month_7','month_8', 'month_9', 'month_10', 'month_11', 'month_12']
FORECAST_HORIZON = 8 # 개월
FREQ = "M"
그런 다음, 데이터셋을 불러옵니다. 데이터셋 설명에 언급된 외부 기능을 이미 포함하고 있습니다.
# 데이터 및 외생적 특징 로드
df = pd.DataFrame(load_dataset("zaai-ai/time_series_datasets", data_files={'train': 'data.csv'})['train']).drop(columns=['Unnamed: 0'])
df[TIME_COL] = pd.to_datetime(df[TIME_COL])
# 월을 원핫 인코딩
df['month'] = df[TIME_COL].dt.month
df = pd.get_dummies(df, columns=['month'], dtype=int)
print(f"고유 ID의 시계열 수: {len(df['unique_id'].unique())}")
df.head()
데이터 세트를로드 한 후, 데이터를 훈련 및 테스트로 분할 할 수 있습니다 (우리는 테스트 세트로 데이터의 마지막 8 개월을 사용하기로 결정했습니다).
# 8 개월 동안 테스트
train = df[df[TIME_COL] <= (max(df[TIME_COL])-pd.DateOffset(months=FORECAST_HORIZON)]
test = df[df[TIME_COL] > (max(df[TIME_COL])-pd.DateOffset(months=FORECAST_HORIZON)]
print(f"훈련을 위한 개월: {len(train[TIME_COL].unique())} from {min(train[TIME_COL]).date()} to {max(train[TIME_COL]).date()}")
print(f"테스트를 위한 개월: {len(test[TIME_COL].unique())} from {min(test[TIME_COL]).date()} to {max(test[TIME_COL]).date()}")
마지막으로, 판다 데이터 프레임을 GluonTS 데이터 세트로 변환하여 모델에 공급해야합니다:
- 훈련 데이터셋(타겟 및 동적 공변량)을 테스트 세트(예측 시간대의 타겟은 null이 됨)의 동적 공변량만을 연결합니다. 그런 다음 팬더스 데이터 프레임의 인덱스를 날짜 열로 바꿉니다.
- 서로 다른 시계열을 구별할 수 있게 해주는 열을 설정합니다(unique_id).
- 미래에 알려진 동적 공변량을 나타내는 열을 정의합니다(feat_dynamic_real).
- 타겟 열(target)과 시계열 주파수(freq)를 정의합니다.
- 모델이 내부적으로 처리하기 때문에 데이터를 스케일링할 필요가 없다는 점을 유의해주세요.
# 팬더스로부터 GluonTS 데이터셋 생성
ds = PandasDataset.from_long_dataframe(
pd.concat([train, test[["unique_id", TIME_COL]+DYNAMIC_COV+SEAS_COV]]).set_index(TIME_COL), # 테스트 동적 공변량과 연결
item_id="unique_id",
feat_dynamic_real=DYNAMIC_COV+SEAS_COV,
target=TARGET,
freq=FREQ
)
데이터셋이 준비되었으니, Moirai를 사용하여 예측할 수 있습니다. 이를 위해 Hugging Face에서 모델을 로드하고 다음 매개변수를 설정해야 합니다:
- prediction_length — 이전에 정의한 예측 시간대입니다.
- context_length — 모델이 주의를 기울일 수 있는 시퀀스의 항목 수(양의 정수).
- patch_size — 각 패치의 길이. 이전에 본 바와 같이 작성자는 빈도에 따라 다른 패치 크기를 설정했습니다. 사전 정의된 값을 사용하려면 patch_size를 'auto'로 설정해야 합니다. 'auto, 8, 16, 32, 64, 128' 중의 하나로 설정할 수도 있습니다.
# 사전 훈련된 모델을 준비하기 위해 huggingface hub에서 모델 가중치를 다운로드합니다.
model = MoiraiForecast.load_from_checkpoint(
checkpoint_path=hf_hub_download(
repo_id="Salesforce/moirai-R-large", filename="model.ckpt"
),
prediction_length=FORECAST_HORIZON,
context_length=24,
patch_size='auto',
num_samples=100,
target_dim=1,
feat_dynamic_real_dim=ds.num_feat_dynamic_real,
past_feat_dynamic_real_dim=ds.num_past_feat_dynamic_real,
map_location="cuda:0" if torch.cuda.is_available() else "cpu",
)
predictor = model.create_predictor(batch_size=32)
forecasts = predictor.predict(ds)
# 예측을 판다스로 변환합니다.
forecast_df = utils.moirai_forecast_to_pandas(forecasts, test, FORECAST_HORIZON, TIME_COL)
예측이 완료되면 실제 값과 예측값을 그래프로 나타낼 수 있습니다.
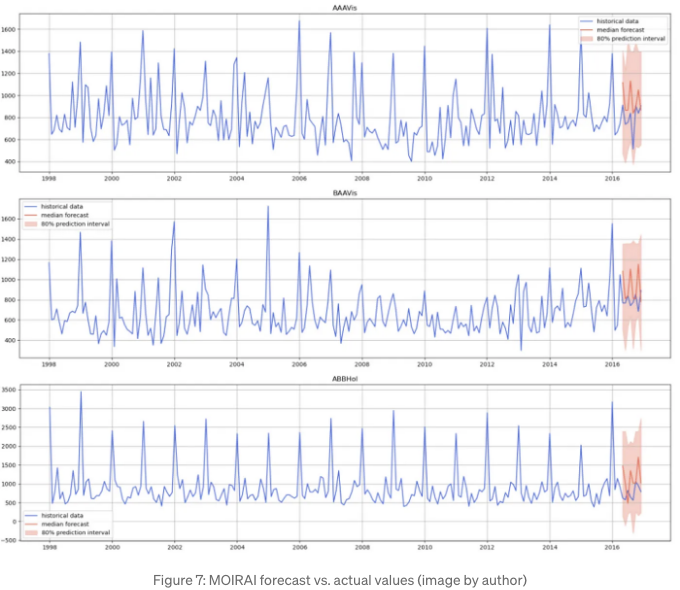
그림 7은 Moirai가 시계열을 예측하는 데 어려움을 겪고 안정적인 예측을 생성하지 못했음을 보여줍니다. 대신, 예상보다 더 높은 크기의 연속적인 점프를 예측했습니다.
Moirai에서 수신한 예측을 기반으로 TiDE 및 Chronos에서 생성된 예측을 불러와서 비교를 위해 예측 성능 지표를 계산할 수 있습니다. 더 잘 이해하기 위해 평균 절대 백분율 오차(MAPE)를 비교 메트릭으로 사용했습니다.
그림 8에서 확인할 수 있듯이 Moirai는 전체 예측 기간에서 가장 높은 MAPE를 가지고 있습니다. 한 달에 있어 TiDE를 약간 능가했지만 결코 Chronos를 능가하지는 못했습니다. 우리는 몇 가지의 비공개 데이터셋에서 유사한 실험을 진행했고 결과는 일관되게 그림 8에 제시된 결과와 일치합니다. 이 일관성은 교육 데이터셋이 공개적으로 공개되지 않았다는 점에서 기초 모델을 분석할 때 관련이 있습니다. 공개 도메인에서 어떤 데이터셋이 그들의 교육 데이터로 사용되었을 수 있다는 것은 가능성이 있습니다. 그러한 상황에서 모델은 단순히 교육 데이터에 오버피팅된 것이었을 수 있습니다.
Chronos는 공변량의 사용을 허용하지 않으며 시계열 간의 독립성을 가정합니다. 이는 Chronos의 접근 방식이 현저히 더 나은 것이며 미래에 발전 가능성이 크다는 것을 보여줍니다.
결론
이 글에서는 시계열 예측을 위한 가장 최근의 재단 모델 중 하나 인 Moirai를 탐구했습니다. 이는 제로샷 추론을 생성할 수 있는 모델의 한 예입니다. 우리는 Chronos와 TimeGPT를 자세히 다뤘는데, Moirai의 접근 방식과 모델 아키텍처는 매우 다릅니다. 따라서 이 모델은 과학적 가치를 지니고 있으며 오픈 소스임에 감사합니다.
우리의 실험 결과는 Moirai가 TiDE와 Chronos를 능가하지 못했음을 나타냈습니다. TiDE의 경우, 그들은 동일한 정보에 액세스하고 TiDE가 특별히 이 데이터에 대해 훈련되었습니다. 그러나 Moirai의 성능을 Chronos와 비교할 때, Moirai로부터 더 비교 가능하거나 심지어 더 나은 성능을 예상했습니다. 왜냐하면 Moirai는 동적 공변량을 통해 외부 정보에 액세스 할 수 있는 이점을 가지고 있으며 서로 다른 시계열 간의 상호 관계에서 이득을 얻을 수 있는 다변량 시계열 모델입니다.
시계열 예측을 위한 기초 모델 개발을 위한 AI 경쟁은 시작에 불과하며, 우리는 그 진행을 주의 깊게 지켜볼 것입니다. 기대해 주세요.
나에 대해
시리얼 기업가이자 AI 분야의 리더입니다. 저는 기업을 위한 AI 제품을 개발하고 AI 중심의 스타트업에 투자합니다.
ZAAI 창립자 | LinkedIn | X/Twitter
참고 자료
[1] Garza, A., & Mergenthaler-Canseco, M. (2023). TimeGPT-1. arXiv. https://arxiv.org/abs/2310.03589
[2] 라술, K., 아쇼크, A., 윌리엄스, A. R., 고니아, H., 바그와트카, R., 코라사니, A., 다르비시 바야지, M. J., 아다모푸로스, G., 리아키, R., 하센, N., 비로쉬, M., 가르그, S., 슈나이더, A., 채파도스, N., 드루앙, A., 잔테데스키, V., 너브리바카, Y., & 리쉬, I. (2024). Lag-Llama: Towards Foundation Models for Probabilistic Time Series Forecasting. arXiv. https://arxiv.org/abs/2310.08278
[3] 다스, A., 공, W., 센, R., & 조우, Y. (2024). A decoder-only foundation model for time-series forecasting. arXiv. https://arxiv.org/abs/2310.10688
[4] 안사리, A. F., 스텔라, L., 터크멘, C., 장, X., 메르카도, P., 셴, H., 셰르, O., 랑가푸람, S. S., 아랑고, S. P., 카푸어, S., 즈시그너, J., 매딕스, D. C., 마호니, M. W., 토르콜라, K., 윌슨, A. G., 보르케-슈나이더, M., & 왕, Y. (2024). Chronos: Learning the Language of Time Series. arXiv. https://arxiv.org/abs/2403.07815
[5] 우, G., 리우, C., 쿠마르, A., 씽, C., 사바레세, S., & 사후, D. (2024). Unified Training of Universal Time Series Forecasting Transformers. arXiv. https://arxiv.org/abs/2402.02592
[6] Palatucci, M., Pomerleau, D., Hinton, G. E., & Mitchell, T. M. (2009). Zero-shot Learning with Semantic Output Codes. In Y. Bengio, D. Schuurmans, J. Lafferty, C. Williams, & A. Culotta (Eds.), Advances in Neural Information Processing Systems (Vol. 22). Curran Associates, Inc. Retrieved from here
[7] Yuqi Nie, Nam H. Nguyen, Phanwadee Sinthong, Jayant Kalagnanam. A Time Series is Worth 64 Words: Long-term Forecasting with Transformers. arXiv:2211.14730, 2022.
[8] Jianlin Su, Yu Lu, Shengfeng Pan, Ahmed Murtadha, Bo Wen, Yunfeng Liu. RoFormer: Enhanced Transformer with Rotary Position Embedding. arXiv:2104.09864, 2021.
[9] David Salinas, Valentin Flunkert, Jan Gasthaus. DeepAR: Probabilistic Forecasting with Autoregressive Recurrent Networks. arXiv:1704.04110, 2017.