
소개
데이터 시각화에서 사용 가능한 캔버스의 크기와 모양은 항상 중요한 요소입니다. 이것은 공간을 절약하기 위한 수단으로 두 축 접근법을 사용하는 Crystal Bar Chart라는 차트를 최근 다른 기사에서 다룬 주제입니다.
이 기사에서는 값을 정사각형으로 시각화하고 볼록 다각형 또는 단순 오목 다각형 형태의 컨테이너를 가득 채우는 공간 절약 방법을 탐구하겠습니다. 또한 이 탐구 과정에 코드를 많이 활용해 보았으니, 다른 유용한 기술과 시각화 유형에 대한 재미있는 자습서로 제공될 수 있기를 희망합니다.
이 기사를 통해 달성하고자 하는 목표는 일반적이고 비표준적인 컨테이너 모양(아래 그림 참조)을 고려하고, 이와 유사한 모양의 값 집합을 제시하여 사용 가능한 공간을 최적화하고 직관적인 크기 비교를 제공하며 데이터를 사각형 모양으로 표현하는 것입니다!
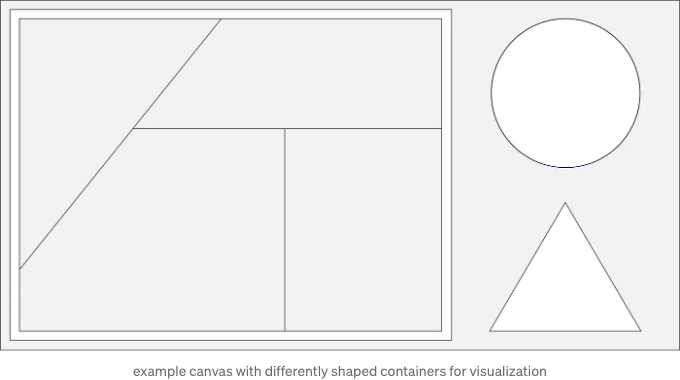
새로운 축 없이 접근하기 전에, 결과를 측정할 좋은 기준을 찾을 수 있는 기존 축 기반 및 축 없는 방법에 대해 생각해 봅시다. 예를 들어, Wikipedia에서 제공하는 동물 중 상위 20마리의 최고 속도를 나타내는 정보를 활용하겠습니다.
축 기반 데이터 시리즈 시각화
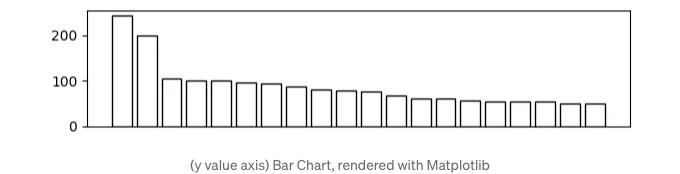
y-축이 항목의 값을 나타내는 경우, 정렬된 막대 차트와 경쟁하기 어려울 수 있어요. 먼저 그것을 플롯하고, 저의 vizmath 패키지를 사용하여 몇 가지 더 축 기반의 차트를 만들어 보겠습니다.
막대 차트
# https://en.wikipedia.org/wiki/Fastest_animals (2024년 1월 26일 기준)
# 20대 최고 빠른 동물 (최고속도, mph)
데이터 = {
'id' : [str(i) for i in range(1, 21)],
'speed' : [242,200,105,100,100,95,92.5,88,80,79,
75,67.85,61.06,60,56,55,55,55,50,50]
}
# 막대 차트 (데이터는 이미 정렬되어 있음)
import matplotlib.pyplot as plt
plt.figure(figsize=(7, 1.5))
막대 = plt.bar(range(1, 21), 데이터['speed'], edgecolor='black',
color='white', linewidth=1)
plt.xticks([])
plt.grid(False)
plt.show()
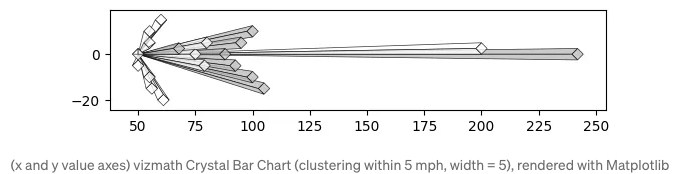
크리스털 막대 차트
from vizmath.crystal_bar_chart import crystals
import pandas as pd
# 데이터: 위를 참조하십시오
df = pd.DataFrame(data)
cbc = crystals(df, 'id', 'speed', height_range=5, width_override=5,
rotation=90, offset=50, bottom_up=True)
cbc.cbc_plot(legend=False, alternate_color=True, color=False)
비스웜 플롯
from vizmath.beeswarm import swarm
import pandas as pd
# 데이터: 위 참조
df = pd.DataFrame(data)
diameter = 5
bs = swarm(df, 'id', 'speed', None, size_override=pi*(diameter/2)**2)
bs.beeswarm_plot(color=False)
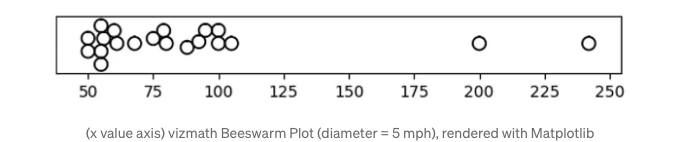
각각의 메소드들은 값의 크기를 반영하는 모양과 위치를 제공하면서 데이터 집합의 밀도 프로필을 제공하는 독특한 방식을 제공합니다.
이제 같은 값 세트를 사용하여 상대적인 크기 비교에 중점을 둔 축 없는 예제로 넘어가며 일부 반응형 Bubble Chart를 그려 Quad-Tile Chart 알고리즘을 미리보겠습니다!
축 없이 데이터 시각화
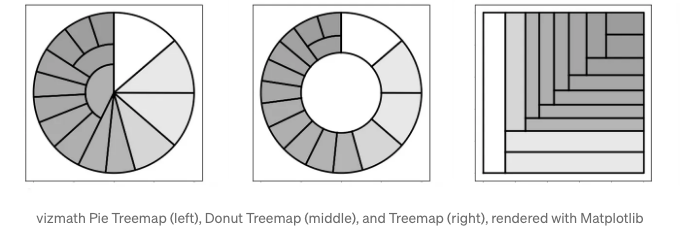
축 없이 도메인을 표현하기 위해 한 수준의 트리맵(저의 Radial Treemap에 관심이 있는 경우 해당 문서를 확인해보세요!)을 포함하고, 이어서 Bubble 차트를 추가해 봅시다.
트리맵 (한 수준의 파이, 도넛, 직사각형)
from vizmath.radial_treemap import rad_treemap as rt
import pandas as pd
# 데이터: 위의 데이터를 참조하세요
# 파이 트리맵
df = pd.DataFrame(data)
o_rt = rt(df, ['speed'], 'speed', r1=0)
o_rt.plot_levels()
# 도넛 트리맵
df = pd.DataFrame(data)
o_rt = rt(df, ['speed'], 'speed')
o_rt.plot_levels()
# 트리맵
df = pd.DataFrame(data)
o_rt = rt(df, ['speed'], 'speed', r1=0, r2=1,
a1=0, a2=1, rectangular=True)
o_rt.plot_levels()
import numpy as np
import pandas as pd
# data: 위에서 참조
df = pd.DataFrame(data)
def grid_bubbles(values, size_by='area', rows=2, cols=10, buffer=0.1):
fig, ax = plt.subplots(rows, cols, figsize=(7, 1.5))
sorted_values = np.sort(values)[::-1]
if size_by == 'area':
sizes = np.sqrt(sorted_values) # 반지름 입력 고려
elif size_by == 'diameter':
sizes = sorted_values # 반지름에 비례
max_size = np.max(sizes)
b = max_size*buffer
max_size += b
index = 0
for i in range(rows):
for j in range(cols):
# Matplotlib의 Circle을 위한 반지름 입력
circle = plt.Circle((0.5, 0.5), sizes[index]/max_size/2,
color='black', fill=False, linewidth=2)
ax[i, j].add_artist(circle)
ax[i, j].set_xlim(0, 1)
ax[i, j].set_ylim(0, 1)
ax[i, j].axis('off')
index += 1
plt.tight_layout()
plt.show()
grid_bubbles(data['speed'], size_by='area')
grid_bubbles(data['speed'], size_by='diameter')

버블 차트 (내 새로운 Quad-Tile 차트 알고리즘을 사용하여 반 정렬)
from vizmath.quadtile_chart import polyquadtile as pq
import pandas as pd
# 데이터: 위를 참조하세요
# 면적에 따라 크기 조정
df = pd.DataFrame(data)
df['speed'] = df['speed']/df['speed'].max()*3.5
o_pq = pq(df,'id','speed',buffer=0.0, collapse=True,
constraints=[(2,1)], auto=False)
o_pq.polyquadtile_plot(show_constraints=True, poly_color='w',
poly_line='black', squares_off=True, circles=True)
print(o_pq.multiplier)
# 지름에 따라 크기 조정
df = pd.DataFrame(data)
df['speed'] = df['speed']**2 # 지름 비율에 맞게 조정
df['speed'] = df['speed']/df['speed'].max()*3.5
o_pq = pq(df,'id','speed',buffer=0.0, collapse=True,
constraints=[(2,1)], auto=False)
o_pq.polyquadtile_plot(show_constraints=True, poly_color='w',
poly_line='black', squares_off=True, circles=True)
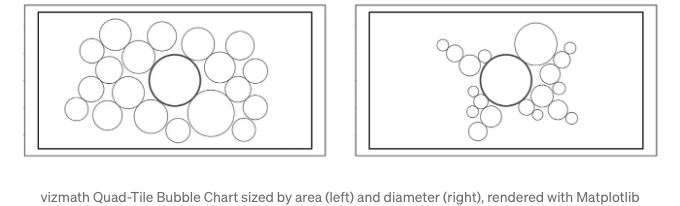
이러한 방법들은 값이 어떤 크기인지 직접적인 참조를 제공하는 축이 없어서 위치 변경 기능이 작동합니다. 따라서 값의 모양, 크기 및 레이아웃이 데이터 인사이트를 수집하는 데 중요합니다. 값 표현 간의 공간을 보존하는 방식으로 이러한 차트를 유용하게 만드는 파라미터 조정이 중요합니다.
숫자 축 기반 차트의 경우 멀리 떨어져 있는 값 모양을 나란히 보여줄 수 있지만, 축 없는 차트를 사용하면 값 모양을 옆으로 보여줄 수 있어요. 데이터와 사용 사례에 따라, 축 없는 방법의 시각화 압축은 축 기반 방법보다 상당한 장점이 될 수 있어요.
위의 버블 차트에서는 면적 및 지름별 크기 설정도 포함했어요. 크기 설정 메커니즘은 종종 간과될 수 있지만, 두 결과 간의 차이는 상당할 수 있어요! 데이터의 성겁과 시각화의 내러티브 맥락에 따라, 시각화 도구에서 크기 설정이 무엇을 기반으로 하는지 항상 알고 있으면, 정보에 기반한 선택을 할 수 있어요.
기본 케이스 (경쟁사)
위의 예시를 리뷰하면 버블 차트가 사용 가능한 공간을 보존하면서 비슷한 형태의 값 세트를 적절히 크기에 맞게 표현하는 우리의 초기 목표를 이루는 경쟁자임을 알 수 있어요.
포장된 Bubble Chart(컨테이너)는 결과를 측정하기 위한 경쟁 상대가 될 것입니다. 그러나 아쉽게도 내가 찾은 구현 (아래에 표시됨)은 원형 레이아웃만 나타내므로 다른 컨테이너 모양을 탐색할 때 완벽한 비교 사례가 되지 않을 것입니다.
# circlify
import circlify
circles_circlify = circlify.circlify(data['speed'], show_enclosure=False)
circles = [c for c in circles_circlify]
max_radius = max(circle.r for circle in circles)
xlim = max(abs(circle.x) + max_radius for circle in circles)
ylim = max(abs(circle.y) + max_radius for circle in circles)
limit = max(xlim, ylim)
fig, axs = plt.subplots(figsize=(8, 8))
axs.axis('off')
plt.xlim(-limit, limit)
plt.ylim(-limit, limit)
for circle in circles:
axs.add_patch(plt.Circle((circle.x, circle.y), circle.r,
edgecolor='black', facecolor='white', linewidth=2))
plt.show()
# packcircles
import packcircles
circles_packcircles = packcircles.pack(data['speed'])
circles = [c for c in circles_packcircles]
# circles
max_radius = max(radius for (_, _, radius) in circles)
xlim = max(abs(x) + max_radius for (x, _, _) in circles)
ylim = max(abs(y) + max_radius for (_, y, _) in circles)
limit = max(xlim, ylim)
fig, axs = plt.subplots(figsize=(8, 8))
axs.axis('off')
plt.xlim(-limit, limit)
plt.ylim(-limit, limit)
for (x, y, radius) in circles:
axs.add_patch(plt.Circle((x, y), radius,
edgecolor='black', facecolor='white', linewidth=2))
plt.show()
# Tableau Public:
import pandas as pd
import os
df = pd.DataFrame(data)
df.to_csv(os.path.dirname(__file__) + '/circles.csv',
encoding='utf-8', index=False)
# select packed bubbles -> Size by [Speed], [Id] on Detail
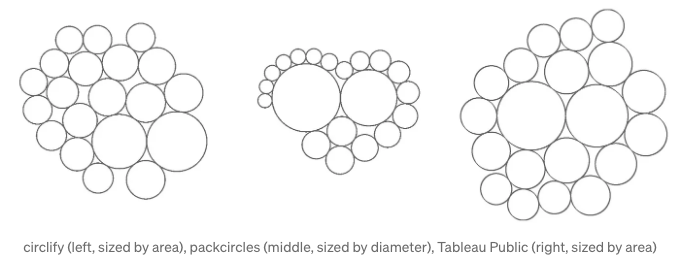
경쟁 상대를 선택했으니 이제 포장된 Bubble Chart가 홀로 서 있는지 또는 컨테이너 포장 목표를 충족하는 상대적 가치 비교를 위해 활용할 수 있는 다른 단순한 모양이 있는지 살펴보겠습니다. 이제 정사각형의 응용을 탐색해 보겠습니다!
왜 Squarify를 사용해야 할까요?
이미 패킹된 원들을 조사하는 무대를 마련했으니, 짧게 쉬어가며 질문을 해보는 게 좋을 것 같아요. 패킹된 원들이 존재하는데 왜 사각형에 관심을 가질까요?
데이터 시각화에서 이미 패킹된 원들이 널리 사용되고 있으므로 사람들은 원을 좋아하는 것으로 보입니다. 다양한 패킹된 버블 차트 구현은 다양한 프로그래밍 언어 및 소프트웨어에서 쉽게 찾을 수 있어요. 사실, Quad-Tile 차트를 만든 후 가장 먼저 한 일은 동그라미를 그리는 데 사용했어요 (소개 부분에 나와 있음). 그래서 동그라미의 매력은 실재해요!
하지만 사각형은 어떨까요? 다른 가능한 모양들과 비교했을 때 패킹된 사각형은 상대적으로 무해해 보이지만, 확실한 패킹된 사각형 차트 구현을 찾는 것은 어렵습니다. 왜 그럴까요...
간단한 비교를 하고 어떤 것을 발견해 봅시다:
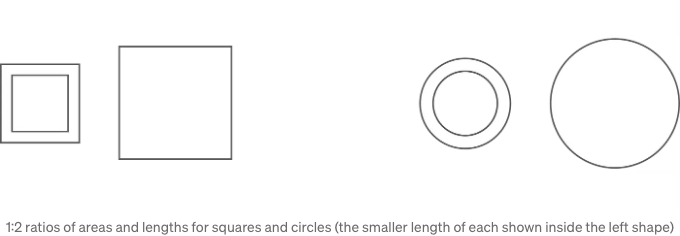
위의 경우 1:2 비율을 사용하여 넓이나 길이를 비교하는 데 둥근 모양이나 사각형 모두 다른 것보다 직관성을 제공하지 않는 것으로 보입니다. 하지만 원은 더 부드럽고 사각형은 더 날카로운 것 같아요.
그렇다면, 나는 스퀘어리파이를 하는 이유가 다음과 같습니다:
- 패킹된 사각형 구현은 존재하지 않는 것 같아서 시각적으로 얼마나 매력적인지 알기가 어렵습니다(패킹된 원의 대체물로). 따라서 조사할 가치가 있습니다.
- 파이썬의 사용 가능한 패킹된 원 구현물에서는 컨테이너를 활용할 수 있는 능력이 일반적으로 부족합니다(모두 원의 수가 증가함에 따라 원형 레이아웃만 제공하는 것으로 보입니다).
- 사각형의 단순성은 알고리즘을 통해 사각형을 채우려고 시도하면 수학적 연산이 직관적일 것으로 보입니다. 따라서 빠른 개념 증명이 가능할 수도 있습니다.
스퀘어화를 추구하는 동기를 제시했으니, 이제 사각형 패킹 노력의 핵심 구성 요소인 패킹을 살펴보고, 사각형이 원에 어떻게 대응하는지 확인해봅시다.
모양 패킹 & 컨테이너 패킹
타일링과 함께
수사 목적으로 명백한 것을 언급할 가치가 있습니다. 사각형은 가장을 가지고 있지만 원은 그렇지 않습니다. 이 특성은 유사한 크기의 사각형들을 테셀레이션할 수 있게 해주어, 패킹이라는 유용한 개념이 될 수 있습니다.
import matplotlib.pyplot as plt
import matplotlib.patches as patches
# 도형과 공간을 사용하여 다이아몬드 테셀레이션 모의실험을 해봅시다.
def diamond_tessellation(rows, cols):
fig, ax = plt.subplots()
ax.set_aspect('equal', adjustable='box')
plt.axis('off')
for row in range(rows):
for col in range(cols):
diamond = patches.Polygon([
(col + 0.5, row),
(col + 1, row + 0.5),
(col + 0.5, row + 1),
(col, row + 0.5)
], edgecolor='grey', facecolor='whitesmoke')
ax.add_patch(diamond)
ax.set_xlim(0, cols)
ax.set_ylim(0, rows)
plt.show()
diamond_tessellation(2, 9)

유감스럽게도, 테셀레이션은 데이터셋의 값이 동일하거나 편리한 비율을 가지는 것으로 가정하는 것이 현실적이지 않기 때문에 일반적인 해결책은 아닙니다. 그러나 간격이 없는 가장의 개념은 원보다 잠재적인 이점으로 더 탐구할 가치가 있습니다.
최적화로
최적화 방법은 두 개의 모양을 비교하는 메커니즘으로 다음 단계로 가치 있는 것처럼 보입니다. 그래서 원과 정사각형 사이에 가능한 균일하게 적용할 수 있는 간단한 목적 함수에 집중하여 결과를 검토해 봅시다.
먼저, 목적 함수의 요소를 식별해야 합니다. 우리는 모양의 중첩을 방지하는 메커니즘과 밀접하게 패킹하려는 반대 힘이 필요합니다. 각각을 자세히 살펴보겠습니다.
- 중첩 방지 (밀어내기) - 중첩을 방지하기 위해 모양들의 총 중첩 영역을 고려하고, 다른 모양에 완전히 포함되는 모양에 대해 추가 벌칙을 부과하여 작은 모양의 중첩 방지를 촉진합니다.
- 패킹 촉진 (가까이 끌어모으기) - 패킹을 촉진하기 위해 모양을 특정 관심 지점으로 끌어당기는 것을 보상할 것입니다.
지금은 컨테이너를 무시하고 도형 패킹에 초점을 맞춰 각 도형의 기하학적 특징을 살펴봅시다. 이제 식별된 재료로 구현할 함수를 설정해 봅시다.
from shapely.geometry import Point, Polygon
from shapely.ops import unary_union
# 셰이프의 중심에서 관심 지점까지의 거리를 더하여 당김 힘을 설정합시다
def calc_distance_from_point(shapes, shape_type, origin):
penalty = 0
ref_point = Point(origin)
if shape_type == 'circle':
for x, y, _ in shapes:
centroid = Point(x, y)
penalty += centroid.distance(ref_point)
elif shape_type == 'square':
for x, y, side in shapes:
centroid = Polygon([(x, y), (x + side, y),
(x + side, y + side), (x, y + side)]).centroid
penalty += centroid.distance(ref_point)
return penalty
# 이제 첫 번째 당김 힘을 설정하여 한 도형이 다른 도형 안에 포함되어 있는지 여부를 파악하고 발생 횟수를 더합시다
def calc_containment(shapes, shape_type):
penalty = 0
shapely_shapes = []
if shape_type == 'circle':
shapely_shapes = [Point(x, y).buffer(r)
for x, y, r in shapes]
elif shape_type == 'square':
shapely_shapes = [Polygon([(x, y), (x + side, y),
(x + side, y + side), (x, y + side)])
for x, y, side in shapes]
for i, shape1 in enumerate(shapely_shapes):
for j, shape2 in enumerate(shapely_shapes):
if i != j and shape1.contains(shape2):
penalty += 1
return penalty
# 당김 힘을 완성하기 위해 전체 도형 중첩 영역을 계산합시다
def calc_overlap_area(shapes, shape_type):
if shape_type == 'circle':
shapely_shapes = [Point(s[0], s[1]).buffer(s[2])
for s in shapes]
elif shape_type == 'square':
shapely_shapes = [Polygon([(s[0], s[1]), (s[0] + s[2], s[1]),
(s[0] + s[2], s[1] + s[2]), (s[0], s[1] + s[2])])
for s in shapes]
merged_area = unary_union(shapely_shapes).area
individual_areas = sum(shape.area for shape in shapely_shapes)
return abs(individual_areas - merged_area)
# 마지막으로, 힘을 종합하여 목적 함수로 만들어봅시다
def objective_function(variables, shapes, shape_type,
origin=(0,0), prevent_overlap_factor=2):
for i, shape in enumerate(shapes):
shapes[i] = (variables[i*2], variables[i*2 + 1], shape[2])
overlap_area = calc_overlap_area(shapes, shape_type)
contained = calc_containment(shapes, shape_type)
sum_distance = calc_distance_from_point(shapes, shape_type, origin)
return overlap_area * prevent_overlap_factor * (1 + contained) + sum_distance
목적 함수에서는 도형의 겹치는 영역을 포함하는 모양의 수와 곱하여 당김 패널티를 집중시키기로 선택했습니다. 그리고 당김 정도를 조절하는 'prevent_overlap_factor' 가중치를 추가했습니다.
이제 목적 함수가 준비되었으니, 이전의 예제 데이터를 사용하여 원과 사각형 패킹 최적화 루틴을 설정해 봅시다.
# 이전 예시 데이터:
data = {
'id' : [str(i) for i in range(1, 21)],
'speed' : [242,200,105,100,100,95,92.5,88,80,79,
75,67.85,61.06,60,56,55,55,55,50,50]
}
# 원하는 크기 창(Window) (계수)와 모양의 반복 가능한 랜덤 위치를 위한 시드를 설정해봅시다.
계수 = 10
시드 = 123
최대속도 = np.max(data['speed'])
np.random.seed(시드)
모양들 = [(np.random.uniform(0, 계수*1.5),
np.random.uniform(0, 계수*1.5),
v/최대속도*계수) for v in data['speed']]
이제, 원과 사각형의 입력을 분리하고 최적화 메서드에 전달할 경계를 추가해봅시다.
import numpy as np
import copy
from math import sqrt
# 각 모양에 대해 최적화하기 위해 복사본을 만듭시다.
원들 = copy.deepcopy(모양들)
사각형들 = copy.deepcopy(모양들)
# 위치를 최적화하기 위해 좌표를 평면으로 펼쳐봅시다
초기_위치 = [val for s in 모양들 for val in s[:2]]
# 이제 각 모양의 경계를 계산하여 최적화 함수에 전달합시다
def calc_bounds(모양들, 모양_유형):
총_면적 = 0
if 모양_유형 == '원':
총_면적 = sum(np.pi * (r**2) for _, _, r in 모양들)
elif 모양_유형 == '사각형':
총_면적 = sum(side**2 for _, _, side in 모양들)
추정된_한변의_길이 = sqrt(총_면적)
패딩 = 추정된_한변의_길이 / 2
하한 = 0 - 패딩
상한 = 추정된_한변의_길이 + 패딩
return (하한, 상한)
# 원과 사각형에 대한 경계 계산
원의_경계 = calc_bounds(원들, '원')
사각형의_경계 = calc_bounds(사각형들, '사각형')
# 각 모양에 경계를 적용하여 최적화하기
원_경계들 = [(원의_경계[0], 원의_경계[1])
for _ in range(len(초기_위치))]
사각형_경계들 = [(사각형의_경계[0], 사각형의_경계[1])
for _ in range(len(초기_위치))]
# 풀 힘을 위한 접힘점을 설정하기 위해 경계를 사용
원의_접힘점 = (원의_경계[1]-원의_경계[0])/2+원의_경계[0]
사각형의_접힘점 = (사각형의_경계[1]-사각형의_경계[0])/2+사각형의_경계[0]
원의_접힘점들 = (원의_접힘점, 원의_접힘점)
사각형의_접힘점들 = (사각형의_접힘점, 사각형의_접힘점)
마지막으로, 결과를 시각화하기 위한 플로팅 함수를 설정하고 각 모양에 대해 최적화를 실행해보겠습니다.
import matplotlib.pyplot as plt
import matplotlib.patches as patches
from math import inf
from scipy.optimize import minimize
# 결과를 확인할 수 있는 plotting 함수를 만들어봅시다.
def plot_shapes(shapes, shape_type):
fig, ax = plt.subplots()
min_x, min_y, max_x, max_y = 0.,0.,0.,0.
for s in shapes:
if shape_type == 'circle':
circle = patches.Circle((s[0], s[1]), s[2],
facecolor='lightgrey', edgecolor='black')
ax.add_patch(circle)
min_x = min(min_x, s[0] - s[2])
min_y = min(min_y, s[1] - s[2])
max_x = max(max_x, s[0] + s[2])
max_y = max(max_y, s[1] + s[2])
elif shape_type == 'square':
square = patches.Rectangle((s[0], s[1]), s[2], s[2],
facecolor='lightgrey', edgecolor='black')
ax.add_patch(square)
min_x = min(min_x, s[0])
min_y = min(min_y, s[1])
max_x = max(max_x, s[0] + s[2])
max_y = max(max_y, s[1] + s[2])
padding = 1
ax.set_xlim(min_x - padding, max_x + padding)
ax.set_ylim(min_y - padding, max_y + padding)
ax.set_aspect('equal', 'box')
plt.show()
# 마지막으로 반복을 모니터링하는 콜백 함수를 설정해봅시다.
def callback(i):
global iteration
iteration += 1
print(f'반복 {iteration}')
# 원 최적화 실행:
iteration = 0
optimized_circles = minimize(objective_function, initial_positions,
args=(circles, 'circle', origin_circles), method='L-BFGS-B',
bounds=bounds_circles, callback=callback,
options={'maxiter': 300, 'maxfun': inf, 'ftol': 0, 'gtol': 0})
packed_circles = [(optimized_circles.x[i*2],
optimized_circles.x[i*2 + 1], circles[i][2])
for i in range(len(circles))]
# plot_shapes(shapes, 'circle') # 초기 위치를 보려면 주석 해제
plot_shapes(packed_circles, 'circle')
# 사각형 최적화 실행:
iteration = 0
optimized_squares = minimize(objective_function, initial_positions,
args=(squares, 'square', origin_squares), method='L-BFGS-B',
bounds=bounds_squares, callback=callback,
options={'maxiter': 300, 'maxfun': inf, 'ftol': 0, 'gtol': 0})
packed_squares = [(optimized_squares.x[i*2],
optimized_squares.x[i*2 + 1], squares[i][2])
for i in range(len(squares))]
# plot_shapes(shapes, 'square') # 초기 위치를 보려면 주석 해제
plot_shapes(packed_squares, 'square')
위 코드에서는 'L-BFGS-B' 메서드를 선택하여 scipy의 'minimize' 함수에서 반복 횟수를 300으로 설정했습니다. 초기 위치를 제어하는 난수 시드는 결과에 영향을 미칠 수 있으므로 두 모양에 대해 각각 3가지 다른 시드를 살펴봅시다.
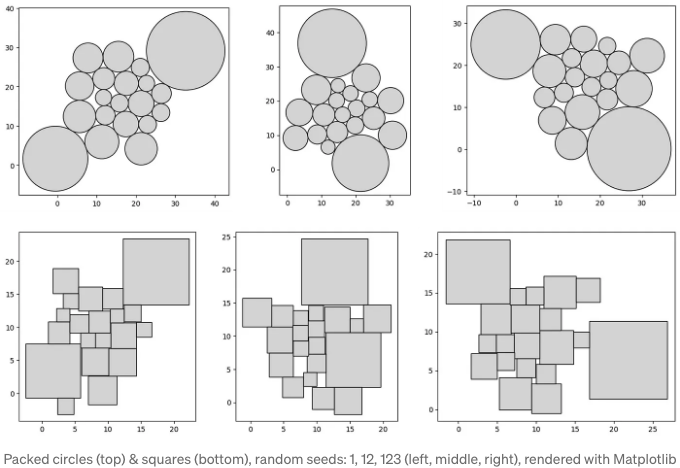
각 테스트 케이스를 생성하는 데 랩톱에서 약 5분이 걸렸으므로, 이 방법의 시간 요구 사항은 고려해야 할 불안정한 요소입니다. 이미 긴 대기 시간 때문에 컨테이너 중첩 비용을 목적 함수에 추가하여 컨테이너 패킹 통찰을 검토하는 것은 현재 필요하지 않은 것으로 보입니다.
지면 배치 관련해서 원들이 더 조밀하게 배열되어 있는 것 같습니다. 이것이 데이터 시각화에서 패킹된 원이 패킹된 정사각형보다 흔한 이유를 설명하는 첫 번째 증거가 될 수 있습니다.
하지만 포기하기 전에, 정사각형에 맞춤화된 알고리즘을 사용한 최종 평가로 넘어가 봅시다!
알고리즘을 통해
위의 실험에서 얻은 주요 결론은:
- 일반 최적화 구현을 사용하여 단순 목적 함수에 따라 패킹된 모양을 생성하는 것은 어느 정도 작동하는 것 같아요.
- 그러나 이것은 정말 느리고 대규모 데이터셋을 처리하기에 부적합하죠.
- 원형 배열들이 (적어도 컨테이너 패킹 없이는) 사각형 배열보다 더 융합되어 보였어요.
우리는 대규모 데이터셋에서 성능이 우수하며 더 매력적인 사각형 배열을 생성할 수 있고, 컨테이너 패킹을 구현할 수 있는 특수화된 알고리즘이 필요하다는 것이 분명해요. 이 방식을 일반적인 최적화 프레임워크와 구분짓기 위해 사각형의 특정 특성을 활용하고, 포장 기회를 탐색할 필요가 있어요.
우리가 활용할 수 있는 사각형의 몇 가지 기하학적 요소를 나열하여 시작해봐요:
- 형태: 네 개의 직각을 감싸고 있는 같은 길이의 네 변을 가지며, 화면을 기준으로 회전할 수 있어 다른 외형이 될 수 있는
- 패킹: 간격 없이 사각형 사이에 이웃할 수 있는 능력
- 배치: 각 사각형의 각 변은 4개의 가능한 꼭지점 중 하나에서 시작하여 이웃할 사각형에게 이웃할 수 있는 평면적인 2차원 공간을 무한대로 제공함
다음에는 패킹된 사각형이 패킹된 원과 어떻게 경쟁할 수 있는지 이해하기 위해 Quad-Tile 차트라는 새로운 시각화 기술에 사용되는 알고리즘을 설명할 것입니다.
Quad-Tile 차트
영감
몇 년 전 어떤 사람이 패킹된 버블 차트는 대부분 쓸모없다고 말했습니다. 무슨 이유에서인지 그 말이 나에게 영감을 주어 패킹된 사각형 차트를 만들게 되었습니다.
첫 번째 버전을 개발하고 Tableau Public 시각화와 몇 가지 다른 기술과 함께 구체화된 결과물을 시험해 보았어요. 여기에는 18개의 사각형을 포함하는 Voronoi Treemaps가 있는 (v1) Quad-Tile Chart가 표시된 발췌본이 있어요. (Voronoi Treemaps는 D3.js를 사용하여 계산되었어요).

아래에서는 이 알고리즘에 대해 설명하고, 몇 일 전에 다시 시작했을 때 최종적으로 채택한 방식을 설명할게요.
(초기) 알고리즘 v1
내 초기 접근 방식인 2022년 초에는 컨테이너를 고려하지 않았습니다. 가장 큰 정사각형부터 시작하여 중앙에 배치한 후 모든 정사각형이 중심 정사각형 주변에 감싸지도록 연속적으로 나열하려고 노력했습니다. 가장 작은 정사각형은 가장 중심부터 먼 위치에 배치되었습니다.
마디 있는 정사각형 배열에 관해 스케치한 후에 나에게 온 개념 중에는 다음과 같은 것들이 있습니다:
- 사분면 - 조사한 결과, 정사각형은 연속적인 사각형들을 분산하기 위한 4개의 오프셋 평면을 제공합니다.
- 자기 조직화 정사각형 배치 - 한 평면의 잠재적 너비와 오프셋 평면의 차지된 높이를 연관시킴으로써 자기 조직화를 가능케하도록 하며, 이는 공유 경계(분할된 세그먼트로 실행됨)를 구현함으로써 이루어집니다.
- 측면 전환 - 크기에 따라 정사각형들을 고르게 분산하기 위해, 원하는 순서로 하나를 배치한 후 측면을 전환합니다. (나는 기본적으로 윗쪽-오른쪽-아래쪽-왼쪽으로 전환했습니다.)
- 사용자 정의 - 이 방법은 값 정렬을 배제하지만, 일련의 규칙에 따라 다음 측면을 선택할 수 있는 기능을 구현할 수 있는 능력을 제공합니다.
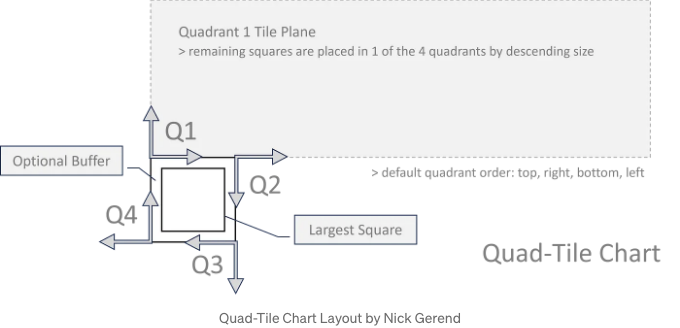
v1 알고리즘은 다음과 같아요:
- 먼저 양수 값들로 이루어진 집합부터 내림차순으로 정렬해요. 예를 들어, 9.4, 7.4, 1.5, 0.2
- 값을 패딩하기 위해 각 사각형 주변의 공간을 추가한 후 (예를 들어 0.5)
- 첫번째 (가장 큰) 사각형을 설정하고, 중앙 사각형 주변의 각 사분면을 위한 세그먼트 저장 메커니즘을 생성해요.
- 초기 세그먼트를 중앙 사각형의 변으로 설정하고, 각 사분면에 하나씩 배정해요.
- 옆면 순서 (기본값은 위, 오른쪽, 아래, 왼쪽)가 주어지면, 각 면을 반복하면서 작은 사각형을 배치해요. 각 사분면의 첫 번째 사각형은 해당 사분면 평면의 원점과 정렬되어, 해당 사분면의 초기 세그먼트 시작 위치에서 시작해요.
- 위쪽 면에 사각형을 배치하려면 (정렬 및 배치 요구 사항을 고려하여), 세그먼트를 가장 짧은 y값별로 정렬하고 가장 긴 길이를 가지는 세그먼트에서, 사각형의 너비 ≤ 세그먼트 길이인 첫 번째 세그먼트에 사각형을 배치해요.
- 사각형을 배치하면, 해당 사각형이 차지한 공간을 세그먼트에서 조절하여 세그먼트의 시작 위치 및 길이를 조정하고, 새로운 세그먼트를 만들어요.
- 배치된 사각형의 시작 위치가 사분면 평면의 오프셋 경계와 정렬되면 (중앙 사각형의 축에 수직인 경계), 중앙 사각형 주변의 자기 조직화 성장을 가능하게 하기 위해 영향을 받는 세그먼트의 세그먼트 길이를 연장해요.
- 원하는 스택 구성을 위해 필요한 측 선택 메커니즘을 구현해요.
- 사각형을 버퍼로 다시 원래 크기로 바꾸고, 원하는 회전으로 사각형을 회전시켜요 (기본값은 45도).
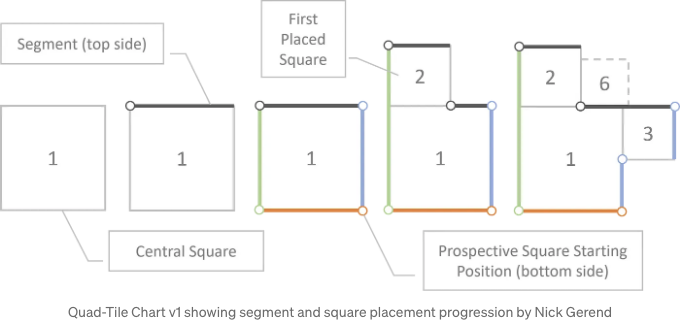
아래 다이어그램은 세그먼트 기반 접근 방법을 보여줘요. 각 세그먼트는 다음과 같이 될 거에요:
- 원래 위치에서 한 방향으로 효과적으로 이동시켜져요 (사각형의 너비가 세그먼트 길이와 같은 경우)
- 두 섹션으로 분할돼요 (하나는 배치된 사각형의 너비를 따르고, 다른 하나는 시작 위치와 길이가 변경된 원래 세그먼트일거에요).
재미로, 몇 가지 측면 선택 옵션을 구현했는데 'constraints' 입력란은 다각형을 받아들이고 외곽을 벗어나면 측면을 전환하려고 시도하여 다각형과 겹치는 특정 영역에서의 성장을 촉진합니다.
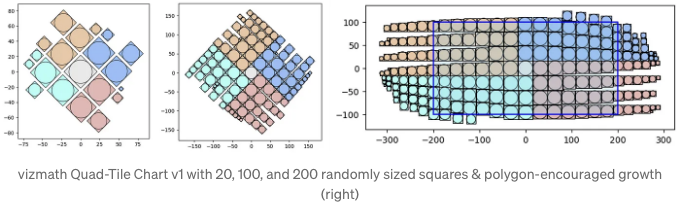
이것이 제 두 번째 영감으로 이어집니다. Quad-Tile Chart v1을 내 vizmath 패키지에 통합할 때 다각형 입력과 더 많은 작업을 할 수 있는지 생각하기 시작했습니다.
일부 실험 끝에, 주어진 다각형 내에 꼭지점이 깔끔하게 맞는 완전히 기능적인 컨테이너 패킹 구현이 재미있을 것이라고 결정하고 처음부터 알고리즘을 완전히 개편해보기로 했습니다! 다음에 해당하는 알고리즘을 확인해 봅시다: Quad-Tile Chart v2
(최종) 알고리즘 v2
이 알고리즘의 두 번째 버전은 v1의 일부 핵심 요소를 확장하고 쿼드런트-세그먼트 접근 방식을 유사하게 사용하면서 몇 가지 수정 사항과 컨테이너 패킹을 수용하기 위한 몇 가지 새로운 기능을 추가합니다.
v2에 대한 주요 세부 내용은 다음과 같습니다. 특별한 점을 확인해 보세요:
- Bridge Segments(컨테이너 채우기)
- Backward Segment Extension(‘축소’ 옵션)
- Value Multiplier Bisection Optimization(컨테이너 패킹)
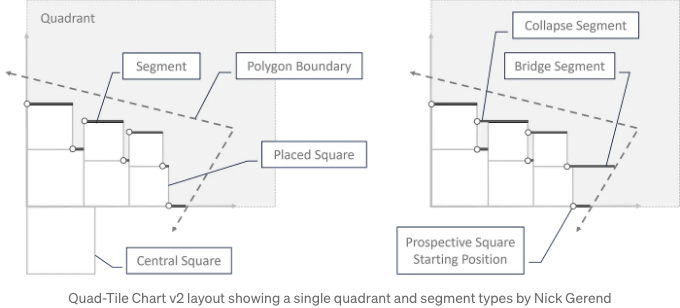
다음은 v2 알고리즘입니다:
- 단계 1~5는 v1과 동일하지만 2가지 세그먼트 속성(세그먼트 높이 및 세그먼트가 활성화되어 있는지), 3가지 사분면 레벨 속성(최소 바닥과 천장 및 해당 사분면 전체가 방을 다 쓴 것인지) 및 배치된 사각형에 대한 속성(왼쪽 아래 모서리 좌표 및 너비)가 추가됩니다.
- 이터레이터(처음에 0으로 설정)가 놓여야 하는 사각형 수보다 작을 동안 다음 절차가 수행됩니다:
- 마지막 바닥 세그먼트(LFS)를 찾습니다: max(segments: 'y=floor', sort: 'x')
- 정렬된 세그먼트 목록을 만듭니다: (segments: 'is active', sort: 'height, x')
- 정렬된 세그먼트를 루프합니다(아래에서 '세그먼트' 및 루프 반복 '세그먼트'로 참조됨) 및 진행합니다.
- 만약 사각형의 모퉁이가 다각형 내에 있고 사각형의 '너비'와 '높이'가 세그먼트의 '너비'와 '높이'에 맞는다면 사각형은 배치됩니다. 그렇지 않으면 세그먼트를 '비활성화'로 설정합니다.
- 세그먼트의 'y' 값이 사분면의 '바닥'과 같다면 사각형의 '너비'를 추가하여 '바닥'을 업데이트합니다.
- 사각형이 배치되면 사각형의 너비와 세그먼트 길이에 따라 현재 세그먼트를 대체할 1개 또는 2개의 새 세그먼트를 생성합니다.
- 축소가 활성화된 경우 다음 절차가 수행됩니다:
- 세그먼트를 새로 생성된 세그먼트 중 가장 왼쪽으로 설정(NLS).
- 확장할 세그먼트를 찾습니다: max(segments: 'x + 길이 = NLS.x', 'y = NLS.y', sort: 'x')
- 확장할 세그먼트가 존재하는 경우, NLS 길이를 추가하고 NLS를 제거합니다.
- 그렇지 않은 경우, 왼쪽 사각형(LS)을 찾습니다: max(squares: 'x+w≤NLS.x', 'y≤NLS.y', 'y+x≥NLS.y', sort: 'x')
- 왼쪽 사각형(LS)이 존재하면 LS.x + LS.w ≤ NLS.x를 확인하여 갭이 있는지 확인합니다.
- 그렇다면, 커버된 세그먼트(CS)를 확인합니다: max(segments: 'y=LS.y', 'x`NLS.x', sort: 'x')
- 커버된 세그먼트가 존재하는 경우, 세그먼트 높이를 사각형 너비와 동일하게 설정하고 병합 세그먼트를 확인합니다: max(segments: 'x+길이+CS.length = NLS.x', 'y=NLS.y', sort: x)
- 병합 세그먼트가 존재하는 경우, 사각형 너비와 CS.length를 추가하여 길이를 확장합니다.
- 그렇지 않은 경우, LS.x + LS.w ≤ NLS.x - 사각형 너비라면 NLS.x = LS.x+LS.w 및 NLS.길이 = CS.length으로 NLS를 조정합니다.
- 세그먼트가 LFS와 같고 배치되지 않았으며 사분면의 바닥이 천장과 다른 경우 다리 세그먼트를 생성합니다. 다음 절차를 따릅니다:
- LFS.높이 및 사분면 바닥을 사분면 천장으로 업데이트합니다.
- 천장 세그먼트(CS)가 천장에서 존재하는지 확인합니다: max(segments: 'y=ceiling', sort: x)
- 존재하는 경우, 그 길이를 다각형 경계까지 확장합니다.
- 그렇지 않은 경우, (세그먼트.x, 천장)에 새 세그먼트를 생성하고 해당 지점과 다각형 경계 사이의 거리로 길이를 설정합니다.
- 마지막으로, 모든 세그먼트를 '활성화'로 설정하고 루프를 종료합니다.
- 그렇지 않은 경우, 사각형이 배치되면 사각형을 사각형 목록에 추가하고 해당 속성을 설정하고 사분면을 '방이있음'으로 설정하고 세그먼트가 마지막 세그먼트인 경우 모든 세그먼트를 '활성화'로 설정하고 이터레이터를 1 증가시키고 다음 측면을 설정하고 루프를 종료합니다.
- 그렇지 않은 경우, 마지막 세그먼트에 도달하면 가능한 경우 더 많은 다리 세그먼트를 추가하려 시도합니다. 다음 절차를 따릅니다:
- 다리 사각형(BS)을 확인합니다: 첫번째(squares: 'x+w=LFS.x', 'y=LFS.y')
- 있으면, LFS.높이 = BS.x로 설정하고 사분면 바닥을 BS.w만큼 증가시키고 사분면 천장을 바닥으로 설정합니다.
- 다리 사각형 세그먼트를 확인합니다: max(segments: 'y=floor', sort: x)
- 하나가 존재한다면, 그 길이를 다각형 경계까지 확장합니다.
- 그렇지 않은 경우, (BS.x+BS.w, 바닥)에 새 세그먼트를 생성하고 해당 지점과 다각형 경계 사이의 거리로 길이를 설정합니다.
- 마지막으로, 모든 세그먼트를 '활성화'로 설정하고 루프를 종료합니다.
- BS를 찾지 못한 경우, 사분면을 '방이없음'으로 설정하고 모든 세그먼트를 '활성화'로 설정하고 다음 측면을 설정하고 모든 사분면이 방이없으면 이터레이터를 놓여야 하는 사각형 수로 설정(사실상 외부 while 루프를 종료합니다).
- v1의 단계 10을 반복하며 각 사분면을 올바른 방향으로 회전합니다.
- 자동 배열 옵션이 선택된 경우(컨테이너 패킹), 변환된 값들
v2 알고리즘은 컨테이너 패킹을 맞추기 위해 훨씬 더 많은 작업을 필요로했기 때문에 v1 알고리즘의 간단함에 비해 더 많은 노력이 필요했습니다. 하지만 정말 그만한 가치가 있었어요! v2에서 몇 가지 레이아웃 예제를 살펴봅시다.

위의 원 형태의 외곽선은 '축소' 기능을 사용하여 참조용으로 포함했습니다. v2의 이론적 한계는 아마도 자기 자신을 내부로 돌리는 다각형들일 것입니다 (이는 사분면의 타일링 평면에서 고유 다각형 갭을 처리하기 위한 향상된 세그먼트 논리가 필요할 것입니다).
다음으로, Python에서 Quad-Tile 차트를 구축하는 방법을 살펴보겠습니다.
파이썬 구현
저는 제 Quad-Tile Chart 알고리즘 v1 및 v2를 파이썬에서 사용할 수 있도록 vizmath 패키지를 통해 구현했습니다. PyPI에서 제공됩니다. 소개에서 시작하는 초기 예제를 사용하여 몇 가지 추가 옵션을 살펴보고 입력 및 출력을 설명하겠습니다. 먼저 v1로 시작합니다:
# Quad-Tile Chart v1
# pip install vizmath==0.0.22
from vizmath.quadtile_chart import quadtile as qt
import pandas as pd
data = {
'id' : [str(i) for i in range(1, 21)],
'speed' : [242,200,105,100,100,95,92.5,88,80,79,
75,67.85,61.06,60,56,55,55,55,50,50]
}
df = pd.DataFrame(data)
# 쿼드타일 객체 생성
# > df: 데이터와 id 필드가 있는 DataFrame
# > id_field: 필수 식별자 필드 (더미값 사용 가능)
# > value_field: 필수 값 열
# > xo: x축 기준점
# > yo: y축 기준점
# > packing: 패킹 방법 ('auto','inc','num','max','min')
# > overflow: 'num', 'max', 'min' 패킹을 위한 정수 임계값
# > buffer: 사각형 크기에 추가 값
# > rotate: 차트 회전 각도
# > constraints: 둘레 내부 성장을 촉진하는 다각형
# > size_by: 'area' 또는 'width'
# > poly_sort: 다각형 정점 정렬 활성화/비활성화 (참, 거짓)
qt_o_area = qt(df,'id','speed', size_by='area', buffer=0)
qt_o_width = qt(df,'id','speed', size_by='width', buffer=0)
# 차트 그리기 (면적 및 너비에 따라 크기 조절)
qt_o_area.quadtile_plot(color='quad', cw=0.75, opacity=.9)
qt_o_width.quadtile_plot(color='quad', cw=0.75, opacity=.9)
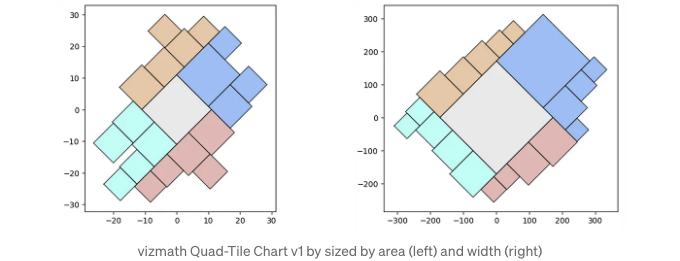
이제 v2를 사용해 봅시다:
# Quad-Tile Chart v2
# pip install vizmath==0.0.22
from vizmath.quadtile_chart import polyquadtile as pqt
import pandas as pd
data = {
'id': [str(i) for i in range(1, 21)],
'speed': [242, 200, 105, 100, 100, 95, 92.5, 88, 80, 79, 75, 67.85, 61.06, 60, 56, 55, 55, 55, 50, 50]
}
df = pd.DataFrame(data)
# 쿼드타일 객체 생성
# > df: 데이터를 포함하고 있는 DataFrame, 숫자형 데이터 컬럼과 id 필드를 가져야 함
# > id_field: 필수 식별자 필드 (더미 값 사용 가능)
# > value_field: 필수 값 컬럼
# > xo: x축 원점
# > yo: y축 원점
# > buffer: 사각형 크기를 조절하는 보정값
# > rotate: 차트 회전 각도
# > sides: 포함시킬 변 선택 ('top', 'right', 'bottom', 'left')
# > collapse: 축소/확대 설정 (True, False)
# > constraints: 패킹할 다각형 컨테이너
# > xc: x축 컨테이너 오프셋 값
# > yc: y축 컨테이너 오프셋 값
# > size_by: 'area' 또는 'width'
# > auto: 자동 패킹 활성화/비활성화 (True, False)
# > auto_max_iter: 자동 패킹 반복 횟수
# > auto_min_val: 자동 패킹 최소 배수
# > auto_max_val: 자동 패킹 최대 배수
# > poly_sort: 다각형 꼭지점 정렬 활성화/비활성화 (True, False)
pqt_o_area = pqt(df, 'id', 'speed', size_by='area', buffer=0)
pqt_o_width = pqt(df, 'id', 'speed', size_by='width', buffer=0)
# 차트 그리기 (면적 및 폭에 따라 사이즈가 지정된 차트)
pqt_o_area.polyquadtile_plot(color='quad', cw=0.75, opacity=0.9)
pqt_o_width.polyquadtile_plot(color='quad', cw=0.75, opacity=0.9)
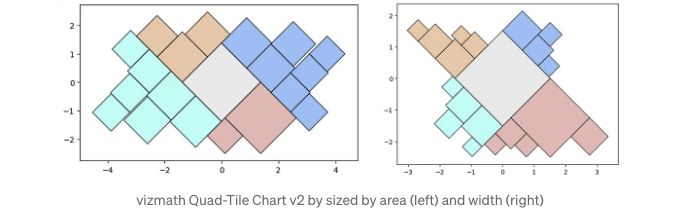
이제 v1 및 v2의 랜덤 초기화 옵션을 포함한 몇 가지 추가 옵션을 조사해 봅시다:
# 1000개의 임의 크기 사각형을 테스트해봅시다:
from vizmath.quadtile_chart import quadtile as qt
from vizmath.quadtile_chart import polyquadtile as pqt
# 상단 좌측에 회전된 Quad-Tile Chart v1
qt_o1 = qt.random_quadtile(1000, rotate=45)
qt_o1.quadtile_plot(color='quad', cw=0.75, opacity=.9)
# 상단 우측에 비회전 Quad-Tile Chart v1
qt_o2 = qt.random_quadtile(1000, rotate=0)
qt_o2.quadtile_plot(color='quad', cw=0.75, opacity=.9)
# 하단 좌측에 정사각형 컨테이너를 사용한 Quad-Tile Chart v2
poly = [(-10,-10),(-10,10),(10,10),(10,-10)] # 다각형 컨테이너
pqt_o1 = pqt.random_polyquadtile(1000, constraints=poly, buffer=0)
pqt_o1.polyquadtile_plot(color='quad', cw=0.75, opacity=.9)
# 중앙에 가로 세로 비율이 1:1인 Quad-Tile Chart v2
pqt_o2 = pqt.random_polyquadtile(1000, constraints=[(1,1)], buffer=0)
pqt_o2.polyquadtile_plot(color='quad', cw=0.75, opacity=.9)
# 하단 우측에 가로 세로 비율이 1:1인 Quad-Tile Chart v2
pqt_o3 = pqt.random_polyquadtile(1000, constraints=[(1,1)],
buffer=0, rotate=0)
pqt_o3.polyquadtile_plot(color='quad', cw=0.75, opacity=.9, circles=False)
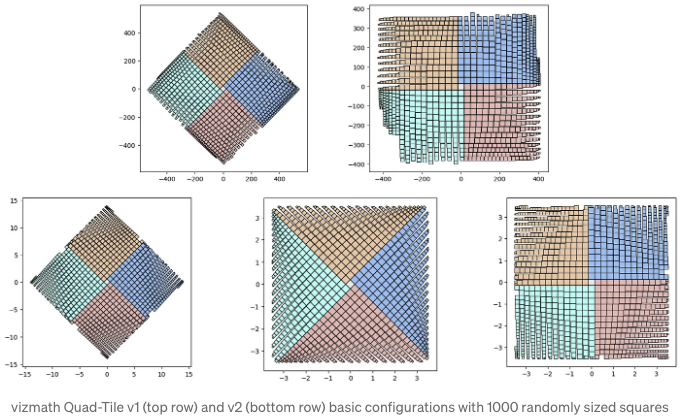
위 내용은 각 버전 간 배치 방법의 미묘한 차이를 보여줍니다 (v1은 y값이 가장 낮고 가장 긴 길이로 선택된 세그먼트, v2는 계단식 접근 방식). 또한 v2에 대한 무작위 초기화는 무작위 볼록 다각형을 생성할 것입니다 — 무엇이 나올지 아무도 모릅니다!
from vizmath.quadtile_chart import polyquadtile as pqt
pqt_o = pqt.random_polyquadtile(100, collapse=True)
pqt_o.polyquadtile_plot(color='quad', cw=0.75, opacity=.9, circles=True,
show_constraints=True)
# 계속해서 무작위 크기 사각형을 사용한 무작위 컨테이너 실행
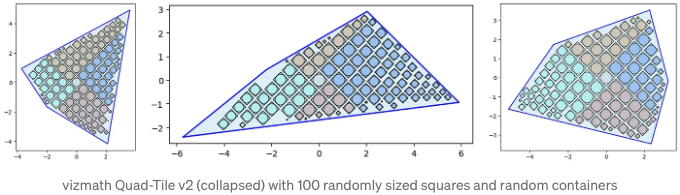
그리고 끝으로, 우리는 중심점을 사용하여 부모 사각형의 경계 상자 크기에 맞는 모든 모양으로 플롯할 수 있음을 기억하세요. 원형 차트의 경우에는 반소형 Bubble Chart만 플로팅한다는 소개를 참조하세요!
이제 Quad-Tile Chart 알고리즘으로 생성된 사분면 다각형과 사분면 중심점 출력을 검토해 봅시다.
사분면 다각형 출력:
- item — ‘id’ 입력 필드로 지정된 수신 식별자
- a — 사각형의 상대적 면적 (버퍼는 포함되지 않음)
- w — 할당된 공간의 너비: 사각형의 너비 + 버퍼*2
- x, y — 레이아웃 내의 점에 대한 직교 좌표
- path — 폴리곤을 둘러싼 경로를 나타내는 정수 순서 집합으로, Crystal Bar Chart의 각 크리스탈 ID 및 면에 대해 각각의 (x, y) 점과 함께 사용됨: 1부터 N까지
from vizmath.quadtile_chart import polyquadtile as pqt
import pandas as pd
# 컨테이너에 맞게 크기 조정 없이 초기 예제 데이터 사용:
data = {
'id' : [str(i) for i in range(1, 21)],
'speed' : [242,200,105,100,100,95,92.5,88,80,79,75,67.85,61.06,60,56,55,55,55,50,50]
}
poly = [(-1000,-1000),(-1000,1000),(1000,1000),(1000,-1000)] # 설명 예제 출력을 위한 충분히 큰 컨테이너
df = pd.DataFrame(data)
o_pq1 = pqt(df,'id','speed',buffer=5.0, collapse=True, constraints=poly, auto=False)
o_pq2 = pqt(df,'id','speed',buffer=5.0, collapse=True, constraints=poly, auto=False, size_by='width')
# 면적에 따라 크기 조정:
o_pq1.o_polyquadtile_chart.df[['id','item','a','w','x','y','path']].head()
# 너비에 따라 크기 조정:
o_pq2.o_polyquadtile_chart.df[['id','item','a','w','x','y','path']].head()
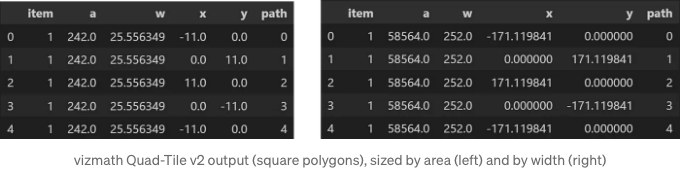
사각형 중심점은 'id' 대신 'item'으로 동일한 속성으로 추출될 수도 있습니다:
넓이 별 크기:
o_pq1.o_polysquares.df[['id','a','w','x','y']].head()
너비 별 크기:
o_pq2.o_polysquares.df[['id','a','w','x','y']].head()
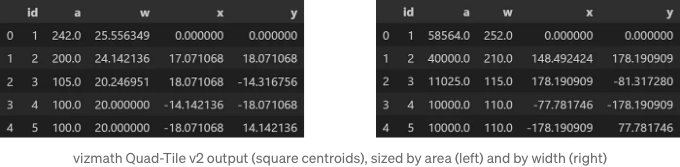
이제 Quad-Tile 차트로 무엇을 더 할 수 있는지 알아봅시다.
확장성
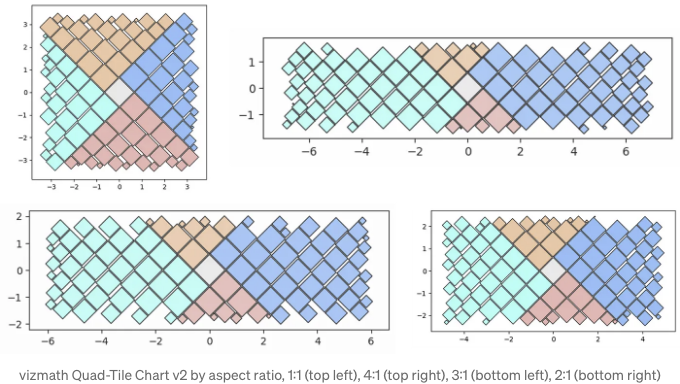
캔버스 레이아웃을 활용하는 원래의 목표를 표준 및 비표준 컨테이너와 함께 다시 살펴보겠습니다. 볼록 다각형과 간단한 오목 다각형을 수용할 수 있는 방법을 보여드렸고, 이제는 소개에서 소개된 레이아웃을 채워봤습니다. 각각 100개의 정사각형이 들어가는 컨테이너에 대해 다양한 회전을 적용했습니다.
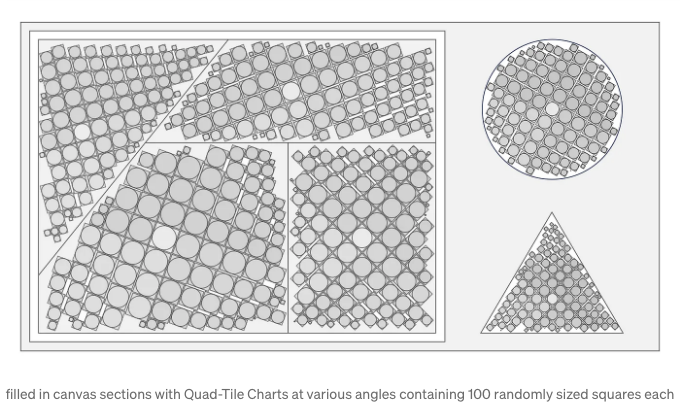
가장 일반적인 캔버스 레이아웃은 직사각형 컨테이너일 것이므로, 원하는 종횡비를 간단하게 전달하는 것이 유용합니다. 다음은 너비를 다양하게 조절한 예시입니다 (높이 조절 방법도 동일합니다):
from vizmath.quadtile_chart import polyquadtile as pqt
aspect_ratio = (1,1) #(2,1) (3,1) (4,1)
pqt_o = pqt.random_polyquadtile(100, constraints=[aspect_ratio],
rotate=45, collapse=True, buffer=.02)
pqt_o.polyquadtile_plot(color='quad', cw=0.75, opacity=.9)
Extensibility의 또 다른 흥미로운 측면은 계층적 데이터를 포함하는 것입니다. 기존 방법의 일부 단점은 다음과 같습니다:
- 중첩된 원은 레벨별로 정확한 상대적인 면적을 유지할 수 없습니다. 이를 위해 중첩된 Radial이나 Voronoi Treemaps가 필요합니다.
- Treemaps는 상위 레벨에서 불규칙한 차원을 가질 가능성이 있습니다. (사각형, 원형, 또는 Voronoi일 경우)
Quad-Tile Chart는 계층의 상위 수준을 유사한 모양으로 캡처하여 초기 크기 비교를 제공함으로써 두 번째 문제를 우아하게 처리할 수 있습니다.🌟
첫 번째 문제에 대해 말씀드리면, 중첩된 Quad-Tile Charts는 중첩된 패킹된 원(타일 섹션에서 언급된대로)과 동일한 단점을 가지고 있지만, 전통적인 직사각형 Treemaps(또는 Voronoi Treemaps)으로 나무 전체에 대한 정확한 면적을 유지하는 대안을 제공합니다. 중첩된 직사각형 Treemaps은 부모 정사각형의 변을 사용하여 보다 직관적인 자식 직사각형 비교를 할 수 있어 원하는 경우가 있습니다.
다음 단계의 직사각형 Treemaps에 대한 예시 몇 가지를 함께 공유드리겠습니다. 상위 수준에 정사각형을 포함한 Quad-Tile Chart에 중첩된 이들을 제가 “Squaremaps”라고 부르겠습니다!
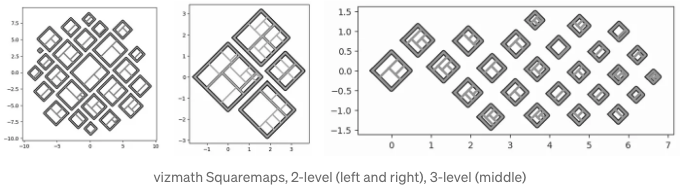
제가 vizmath에서 Squaremaps에 대한 구현을 다음과 같이 작성했습니다(그리고 필요 시 계층적 데이터를 동적으로 생성하는 기능도 추가했습니다!):
import pandas as pd
from vizmath.quadtile_chart import squaremap as sm
# 랜덤한 스퀘어 맵 생성
o_sm1 = sm.random_squaremap(num_levels=3, items_range=(2,4),
value_range=(1,1000), sig=0.8)
o_sm1.o_squaremap.plot_levels(level=3, fill='w')
# 계층적 데이터를 사용하여 스퀘어 맵 생성
data = [
['a1', 'b1', 'c1', 9.3],
['a1', 'b1', 'c2', 6.7],
['a1', 'b1', 'c3', 2.4],
['a1', 'b2', 'c1', 4.5],
['a1', 'b2', 'c2', 3.1],
['a2', 'b1', 'c1', 5.9],
['a2', 'b1', 'c2', 32.3],
['a2', 'b1', 'c3', 12.3],
['a2', 'b1', 'c4', 2.3],
['a2', 'b2', 'c1', 9.1],
['a2', 'b2', 'c2', 17.3],
['a2', 'b2', 'c3', 6.7],
['a2', 'b2', 'c4', 4.4],
['a2', 'b2', 'c5', 11.3],
['a3', 'b1', 'c1', 7.5],
['a3', 'b1', 'c2', 9.5],
['a3', 'b2', 'c3', 17.1],
['a4', 'b2', 'c1', 5.1],
['a4', 'b2', 'c2', 2.1],
['a4', 'b2', 'c3', 11.1],
['a4', 'b2', 'c4', 1.5]]
df = pd.DataFrame(data, columns = ['a', 'b', 'c', 'value'])
o_sm2 = sm(df, ['a','b','c'], 'value', constraints=[(1,1)], buffer=.2)
o_sm2.o_squaremap.plot_levels(level=3, fill='w')
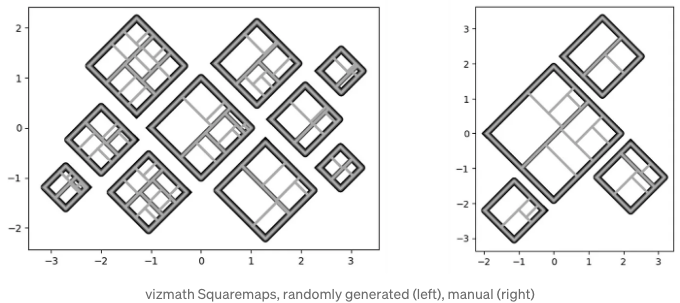
Tableau Public Implementation
파이썬에서 Quad-Tile Chart를 소개했으며 계층적 확장에 대한 Squaremap을 포함하였습니다. 이어서 Tableau Public (v 2023.3.1)에서 양쪽 모두를 구현하는 방법을 보여드리겠습니다! 우선 간단한 Squaremap 구현부터 시작하여 대화형으로 만드는 더 체계적인 Quad-Tile Chart 구축으로 넘어가보겠습니다.
Tableau Public에서 Squaremap 구현
더 자세한 안내를 위해서는, 저의 Radial Treemaps에 관한 글이 있습니다. 해당 글은 상호작용 가능한 계층을 만드는 방법에 대해 더 상세히 안내하며, 이를 위해 Squaremap과 동일한 그림 출력을 사용합니다! 지금은 임의의 입력을 생성하고 단순한 Tableau 예제에 대비한 그림 출력 데이터를 준비해보겠습니다.
from vizmath.quadtile_chart import squaremap as sm
# 임의의 계층 데이터 생성 및 Squaremap 작성
o_sm = sm.random_squaremap(num_levels=3, num_top_level_items=120,
items_range=(2,4), value_range=(1,10), sig=0.75,
collapse=True, buffer=0.05)
# 초기 플롯 검토
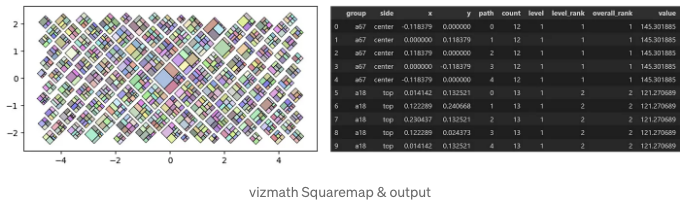
o_sm.o_squaremap.plot_level(level=3)
# 출력의 미리보기 (그림 데이터)
o_sm.o_squaremap.df_rad_treemap.head(10)
# 데이터로 그림 객체 설정
o_sm.o_squaremap.o_rad_treemap.df = o_sm.o_squaremap.df_rad_treemap
# Tableau에서 지도 레이어를 활용하기 위한 데이터 재조정
o_sm.o_squaremap.o_rad_treemap.dataframe_rescale(
xmin=-5, xmax=5, ymin=-5, ymax=5)
# 데이터를 csv로 작성
o_sm.o_squaremap.o_rad_treemap.dataframe_to_csv('squaremap')
테이블 태그를 Markdown 형식으로 변경해주세요.
- [Group]을 Marks 아래 Detail로 드래그하세요.
- Marks 드롭다운 메뉴에서 Polygon을 선택하세요 (이 시점에서 이상하게 보인다고 걱정하지 마세요).
- [Path]를 Marks 아래 Path로 드래그하고 현재 SUM(Path)인 항목을 우클릭하여 Dimension으로 선택하세요.
- [Value]를 Color로 드래그하고 Dimension으로 변환하는 작업을 반복하세요.
- Color 아래에서 "색상 편집..."을 선택하고 다음 옵션으로 구성하세요: '반전, 고급: (시작: 0, 끝: 10)'
이제 더 재미를 위해 더 한 개의 레이어를 추가하여 색상을 변경해 봅시다:
- [Treemap]을 지도 영역으로 드래그하면 팝업이 나타납니다: Marks 레이어 추가 - 이를 클릭하여 새로운 지도 레이어를 생성하세요.
- 위의 단계를 반복하되 이제 [Side]를 Color로 사용하세요.
- Color 아래에서 검은 테두리를 선택하고 투명도를 15%로 설정하세요.
이제 아래와 유사한 차트가 나타날 것입니다 (입력의 무작위성으로 인해 고유한 것이 될 것입니다!). 이제 [Level]로 필터링하거나 필요에 맞는 상호 작용을 설정할 수 있습니다.
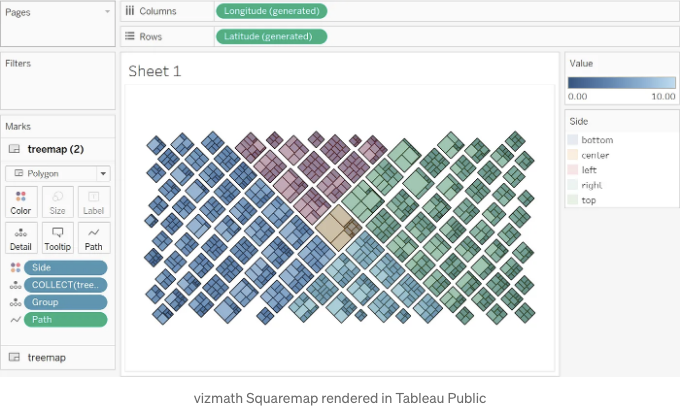
이 Squaremap 구현이 당신의 계층적 데이터를 더 자세히 탐색하는 데 유용한 시작점이 되길 바랍니다!
Tableau Public에서 Quad-Tile Chart 구현
이제 더 자세한 Quad-Tile Chart 구현에 초점을 맞추고 Tableau Public에서 상호작용형 시각화를 만들어 보겠습니다. 강 체계에 대한 위키피디아 데이터 일부로 시작해서 파일에 저장해보죠.
import pandas as pd
# 위키백과에서 (2024년 1월 26일 기준) 상위 50개의 강 시스템 목록
# https://en.wikipedia.org/wiki/List_of_river_systems_by_length
data = {
'강' : [str(i) for i in range(1, 51)],
'길이_km' : [
6650,6400,6300,6275,5539,5464,5410,4880,4700,4444,4400,4350,4241,
4200,3969,3672,3650,3645,3610,3596,3380,3211,3185,3180,3078,3060,
3058,3057,2989,2888,2809,2740,2720,2704,2620,2615,2570,2549,2513,
2500,2490,2450,2428,2410,2348,2333,2292,2287,2273,2270],
'길이_m' : [
4130,3976,3917,3902,3445,3395,3364,3030,2922,2763,2736,2705,2637,
2611,2466,2282,2270,2266,2250,2236,2100,1995,1980,1976,1913,1901,
1900,1900,1857,1795,1745.8,1703,1700,1690,1628,1625,1597,1584,
1562,1553,1547,1522,1509,1498,1459,1450,1424,1421,1412,1410],
'배수지역_km2' : [
3254555,7000000,1800000,2980000,2580000,745000,2990000,2582672,
3680000,1855000,2490000,810000,1790000,2090000,712035,1061000,
950000,1380000,960000,884000,1485200,63166,850000,610000,219000,
324000,1030000,570000,473000,817000,404200,1330000,454000,1024000,
534739,242259,1093000,900000,644000,270000,1547,1522,1509,1498,
1459,1450,1424,1421,1412,1410],
'평균유출량_m3_s' : [
2800,209000,30166,16792,18050,2571,12475,22000,41800,11400,15500,
16000,10300,5589,19800,767,13598,8080,7160,856,31200,8400,6210,
3300,703,3153,10100,82,3600,7130,13000,4880,1480,12037,1400,6000,
2575,4300,3800,270000,1547,1522,1509,1498,1459,1450,1424,1421,
1412,1410],
'방출지' : [
'지중해','대서양','동해','멕시코만',
'카라해','보해','오블만','리오데라플라타',
'대서양','오호츠크해','랩테프해','남중국해',
'보퍼트해','기니만','간지스','남쪽의해',
'대서양(마라조 만), 아마존 델타','카스피해',
'아라비아해','페르시아만','아마존','아마존','베링해',
'대서양','아랄해','안다만해','세인트로렌스만',
'멕시코만','예니세이강','흑해','안다만해',
'모잠비크해협','레나강','벵갈만','아랄해','아마존',
'헛슨만','파라나강','동시베리아해','파라과이강','옵강','이르티시강',
'카스피해','아마존','미시시피강','캘리포니아만',
'랩테프해','흑해','레나강','콩고'],
'이름': [
'나일–화이트나일–카게라–냐바롱고–모고고–루카라라',
'아마존–우카야리–탐보–에네–만타롤',
'창강–금샤강–통티안강–당쿠강 (장강)',
'미시시피–미주리–제퍼슨–비버헤드–레드락–헬로링',
'예니세이강–앙가라강–셀렝가강–이더','황허강',
'오블강–이르티시강','리오데라플라타–파라나강–리오그란데',
'콩고강–잠베시 (자이료)',
'두문강–아르군강–헤를런 (흑룽강)','레나강','메콩 (랑창강)',
'맥케너지강–스레이브강–피스강–핀레이','니제르강','브라마푸트라–얀룽창포',
'머리–달링–컬고아–발론–콘다믄','토칸찐스–아라구아이아',
'볼가','인다스–생거 장보','샤트알아랍–유프라테스–무랏',
'마데이라–마모레–그랜데–케인–로차','푸르스','유곤','상프란시스코',
'시르다리야–나린','살윈 (누강)',
'세인트로렌스–나이아가라–디트로이트–세인트클레어–세인트\
메리스–세인트루이스–노스 (그레이트레이크스)','리오그란데','하횡강',
f"도나우–브렉','두네르','두롱강–납마이강–둘롱강–케라올올루–가다쿠",
'잠베지 (잠베지)','빌류이','간지스–후글리–팜다 (강가)',
'아무다리아–판즈','자푸라 (까퀘타)','넬슨–사스카추완',
'파라과이 (리오파라과이)','콜룸마','필코마요','상횡강–카툰',
'이심','우랄','주루아','아칸소어스','콜로라도 (미 서부)',
'올레니오크','드니프르','알단','우방기–우엘']
}
df = pd.DataFrame(data)
df.to_csv('강_시스템.csv')
길이 (
이것은 좋아 보이네요. Tableau에서 지도 레이어를 활용하기 위해 차트 다각형 및 중심점의 출력 데이터를 저장해봅시다. 나중에 사용할 삼각형의 좌표도 출력하여 나준합니다.
# 출력 파일 (Tableau에서 지도 레이어를 활용하기 위해 데이터 재조정)
# Quad-Tile 차트 다각형 출력
o_pqt.o_polyquadtile_chart.dataframe_rescale(-3,3,-2,4)
o_pqt.o_polyquadtile_chart.df = pd.merge(
o_pqt.o_polyquadtile_chart.df, df, left_on='item', right_on='river')
o_pqt.o_polyquadtile_chart.df = o_pqt.o_polyquadtile_chart.df[
['river','side','x','y','path','length_km','length_m',
'drainage_area_km2','average_discharge_m3_s','outflow','name']]
o_pqt.o_polyquadtile_chart.dataframe_to_csv('quadtile')
# Quad-Tile 차트 중심점 출력
o_pqt.o_polysquares.dataframe_rescale(-3,3,-2,4)
o_pqt.o_polysquares.df = pd.merge(
o_pqt.o_polysquares.df, df, left_on='id', right_on='river')
o_pqt.o_polysquares.df = o_pqt.o_polysquares.df[
['river','side','x','y','length_km','length_m',
'drainage_area_km2','average_discharge_m3_s','outflow','name']]
o_pqt.o_polysquares.dataframe_to_csv('quadtile_centroids')
# 삼각형 컨테이너 좌표
poly = o_pqt.constraints
rs_poly_yx = [(vf.rescale(y, -2, 4, -1, 1),
vf.rescale(x, -3, 3, -1, 1)) for x,y in poly]
print(rs_poly_yx)
# 결과:
# [(-0.691813852924281, -0.9166666666666669),
# (0.8615194804090525, 0.0),
# (-0.691813852924281, 0.9166666666666667)]
마지막으로, 상호 작용을 더 활성화하기 위해 범례를 생성해봅시다.
#%% 범례 플롯
df_legend = df.groupby('outflow')['name'].count().reset_index()
o_pqt_legend = pqt(df_legend,'outflow','name',
constraints=[(4,1)], collapse=True,
rotate=45, buffer=.1, size_by='width', sides=['top','right'])
o_pqt_legend.polyquadtile_plot(show_constraints=True)
#%% 범례 데이터
o_pqt_legend.o_polyquadtile_chart.dataframe_rescale(-2,6,-4,4)
o_pqt_legend.o_polyquadtile_chart.df = pd.merge(
o_pqt_legend.o_polyquadtile_chart.df, df_legend,
left_on='item', right_on='outflow')
o_pqt_legend.o_polyquadtile_chart.df = o_pqt_legend.o_polyquadtile_chart.df[
['outflow','side','x','y','path','name']]
o_pqt_legend.o_polyquadtile_chart.dataframe_to_csv('quadtile_legend')
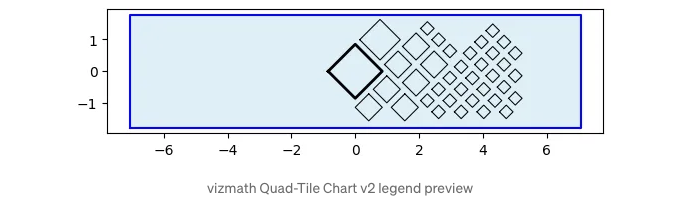
이제 Tableau를 준비했으니, 다음 3개 파일을 모두 가져오기 위해 텍스트 파일 옵션을 사용하여 시작해보겠습니다. Sheet 1로 이동한 다음, 상단 왼쪽 데이터 탭에서 쿼드타일 데이터 소스를 선택하고 다음과 같은 계산 열을 생성하세요:
먼저 맵 영역에서 마우스를 오른쪽 클릭하여 배경 레이어를 선택하고 다음 옵션을 조정해보세요:
- 모든 배경 맵 레이어 (베이스, 랜드 커버 등)을 선택 해제하세요.
- 이제 맵 영역에서 마우스를 오른쪽 클릭하고 맵 옵션을 선택한 다음, 패널에서 모든 옵션을 선택 해제하세요.
배경 레이어를 닫고 다음 단계를 계속해 보세요:
- [Side]를 Marks 하위에 Detail로 드래그합니다.
- Marks 드롭다운 메뉴에서 Polygon을 선택합니다.
- Color 하위에서 검은색 테두리 색상을 선택하고 불투명도를 40%로 조절한 다음 색상을 연한 파랑색으로 설정합니다.
다음으로, 사각형에 대한 윤곽선 레이어를 추가해 봅시다:
- [Squares]를 맵 영역으로 드래그하면 팝업이 나타납니다: Marks 레이어 추가 - 이를 클릭하여 새 맵 레이어를 만듭니다.
- 팝업 메뉴에서 드롭다운 메뉴를 통해 필드를 'Outlines'로 이름을 변경합니다.
- [River]를 이 새로운 맵 레이어의 Marks 하위 Detail로 드래그합니다.
- Marks 드롭다운 메뉴에서 Line을 선택합니다 (이 시점에서 이상하게 보인다 해도 걱정하지 마세요).
- [Path]를 Marks 하위 Path로 드래그하고 차원으로 변환하는 프로세스를 반복합니다.
메인 스퀘어 레이어에 대해 Marks 드롭다운 메뉴에서 Polygon을 선택하여 새 레이어에 대해 위 과정을 반복하고, [Drainage Area Km2]로 색을 입힙니다. '시작: 0, 끝: 3,000,000'으로 설정해주세요.
마지막으로, 데이터 탭에서 quadtile_centroids를 선택하여 중심점을 사용하는 레이어를 추가하고, 다음과 같은 계산된 열을 추가해주세요:
Tableau에서 올바른 크기 조정을 위해 길이를 제곱한 것을 알 수 있습니다. 이를 다음 단계에서 사용할 것입니다:
- [Centroids]를 지도 영역으로 드래그하면 팝업이 표시됩니다: Marks 레이어 추가 - 피말을 해당 위치에 드래그하여 새 지도 레이어를 생성합니다.
- 이 새 지도 레이어에서 Marks 아래 Detail로 [River]를 드래그합니다.
- Marks 드롭다운 메뉴에서 Circle을 선택합니다.
- [Size]를 Marks 아래 Size로 드래그하고 이를 차원으로 변환하는 과정과 크기 틱을 두 번째 해시로 설정합니다.
- [Average Discharge M3 S]를 Color로 드래그하고 하얀 테두리를 추가하고 '시작: 0, 끝: 50,000'으로 설정해주세요.
오른쪽 하단에 널 경고 표시가 나타납니다. 이를 마우스 오른쪽 단추로 클릭하고 숨김 표시를 선택할 수 있습니다. 이 시점에서 상호작용 및 레이블을 나중에 구현하기 위해 아래에 표시된 몇 가지 다른 세부 정보와 속성을 추가한 것처럼 보일 것입니다:

이제 대시보드의 소스 자료를 완성하기 위해 세 개의 시트를 추가해 보겠습니다. 설정을 위해 이미지를 참조하십시오.
- "Bars" - quadtile_centroids 데이터 소스를 사용します.
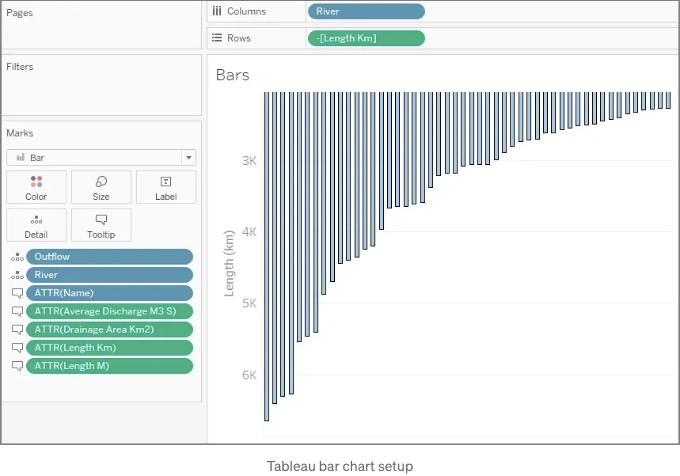
- “범례” - quadtile_legend 데이터 소스 사용
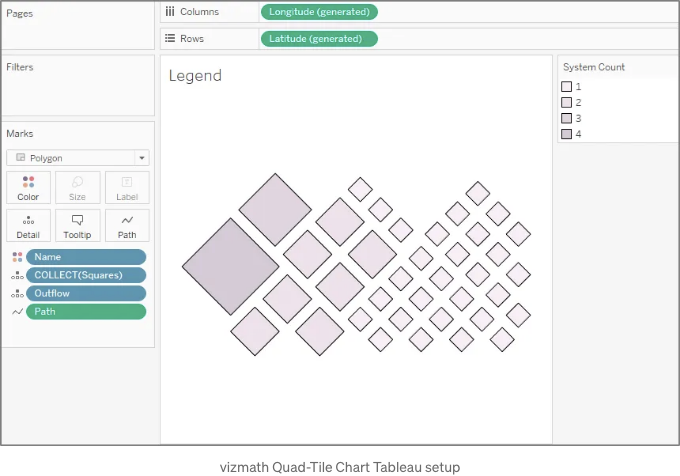
- “강” - quadtile_centroids 데이터 소스 사용, [이름]을 '정렬 기준: 필드, 정렬 순서: 내림차순, 필드 이름: [길이 Km], 집계: 최대값'으로 정렬 ('이름' 항목을 오른쪽 클릭하여 정렬... 선택)
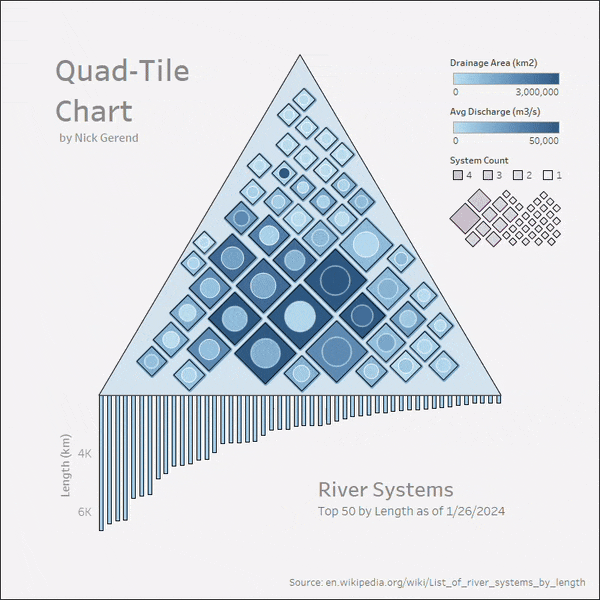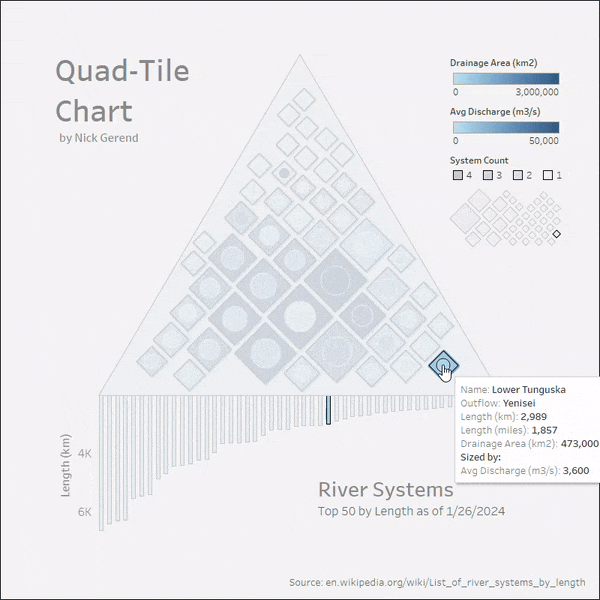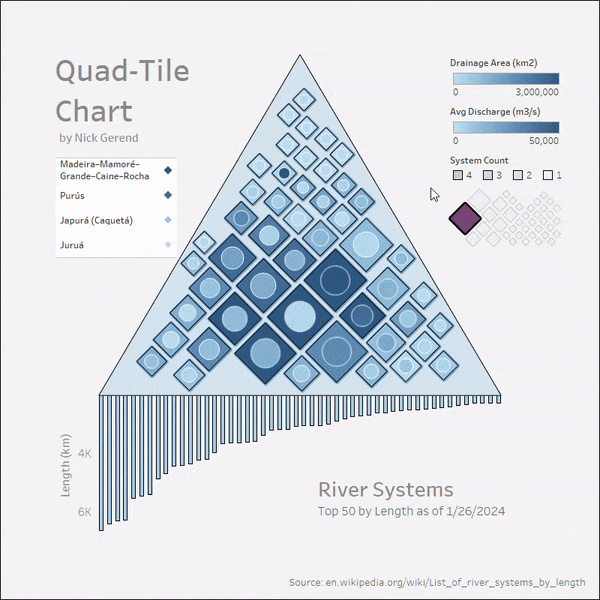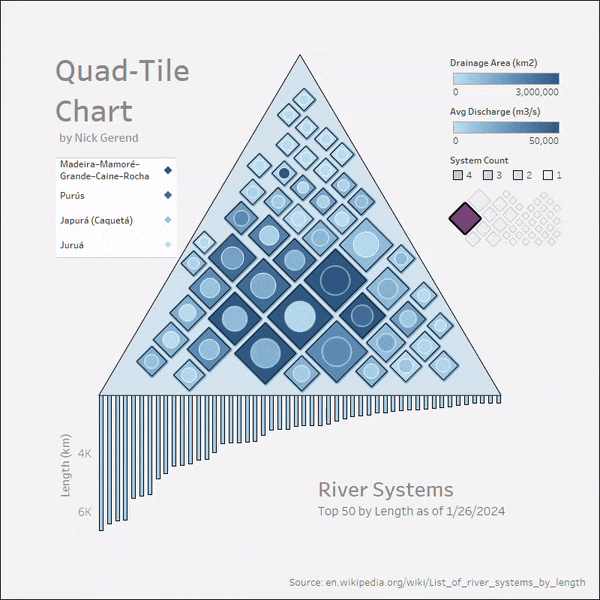
마지막 단계로, 이제 4개의 시트를 대시보드에 정리하고 대시보드 동작 아래의 상단 메뉴에서 몇 가지 동작을 설정해보겠습니다. 대시보드 동작 아래의 추가 동작 드롭다운을 클릭하고 하이라이트를 선택합니다. 대상 하이라이트에서 선택한 필드를 선택하고 [Outflow]과 [River] 필드를 선택합니다 ([Outflow]가 상기 시트에 세부사항으로 추가되었는지 확인). 마지막으로 오른쪽 상단의 실행 동작 아래에서 가리키기 옵션을 선택합니다.
마지막 동작으로 추가 동작 드롭다운을 클릭하고 다음 옵션을 사용하여 필터를 선택합니다: '소스 시트: 범례, 대상 시트: 강, 선택한 필드: Outflow quadtile_centroids Outflow, 실행 동작: 선택시 실행, 선택 해제 시 모든 값 제외'. 이제 대시보드는 모든 시트에서 요청시 하이라이트를 표시하고 범례 시트에서 선택된 값에 대해 필터를 제외할 것입니다!
결론
이 글에서 우리는 정방형이 원에 비해 채워진 도형 시각화에서 어떻게 성능을 발휘할 수 있는지 알아보기 위한 여정을 떠났습니다. 저희는 정방형의 적용을 테스트하기 위해 고수준 비교를 위한 최적화 프레임워크를 구현했고, 결국 정방형의 잠재력을 최대한 활용하기 위해 사용자 정의 알고리즘을 활용하기로 결정했습니다.
저는 "쿼드-타일 차트"라고 명명한 것에 대한 상세한 안내서를 제공합니다. 이 차트는 값 세트를 시각화하는 데 사용되며, 또한 값 계층 구조를 시각화하거나 시각화 캔버스의 사용 가능한 공간을 고려해 원하는 다각형 컨테이너 내에 정방형을 패킹하는 기능을 제공하는 "스퀘어맵"으로 확장됩니다.
현재 데이터 시각화 공간에서 사용되는 주요 원 패킹 구현과는 다르게 다각형 컨테이너는 주요 장점으로 작용하며, Squaremap을 통해 계층 데이터는 새로운 집을 찾을 수 있습니다.
가능하면, Quad-Tile Chart의 사각형 배열은 시각적으로 매력적으로 보입니다 (원과 경쟁하기 위해 필수적입니다!) 그리고 사각형은 원의 중심에 배치된 원들과 서로 바꿔 쓸 수 있습니다 (반응형인 Bubble Chart를 위해) 이것은 데이터를 사각형으로 구성하는 경향을 정당화하기 위한 우리의 노력의 승리로 결론내릴 수 있습니다.
각종 데이터 시리즈와 계층이 모든 코너를 도발하고 있을 때, 여러분이 이러한 시각화 기술을 데이터 탐색 여정에서 유용한 도구로 활용하길 바랍니다!
참고 자료
본 문서에 포함된 모든 이미지는 별도로 명시하지 않은 한 저자가 제작했습니다.
[1] 위키백과 (CC BY-SA), “최고의 빠른 동물” (기준일: 2024년 1월 26일)
[2] 위키백과 (CC BY-SA), “길이별 강 시스템 목록” (기준일: 2024년 1월 26일)
관련 기사
- 복잡한 집합 관계를 시각화하는 Multi-Chord Diagram 소개