기계 학습 전문가로서, 보통 데이터셋(X, y)을 갖고 있고, M이라고도 불리는 함수를 찾고 싶어합니다. M(X) ≈ y를 만족하는 함수입니다. 보통, 우리는 M의 함수 형태에 크게 신경 쓰지 않습니다. 우리 관점에서는, 모델이 신경망, 트리 기반 알고리즘 또는 완전히 다른 것이든 간에 테스트 세트에서 좋은 성능을 보이면 만족합니다.

하지만, 이러한 복잡한 모델을 사용하면 흥미로운 패턴이나 때로는 데이터 내에 잠재된 물리학이나 경제법칙을 놓칠 수 있습니다. 더 나은 결과를 얻기 위해, Symbolic Regression을 사용하여 모델을 구축하는 방법을 보여드리겠습니다. 이러한 모델은 소수의 항만으로 구성되어 어디서든 쉽게 구현할 수 있습니다. 이것이 무엇인지 살펴볼까요?

물리학 실험

실험 물리학자로서 지정한 높이 h에서 물체를 떨어뜨렸을 때 땅에 도달하는 데 얼마나 걸리는지 알아보고 싶습니다. 예를 들어, h = 1.5m의 높이에서 (공기 저항에 영향받지 않을만큼 충분히 무거운) 물체를 떨어뜨린다면, 땅에 도달하는 데 약 0.55초가 걸립니다. 한 번 시도해보세요!

그러나 이는 지구나 중력 가속도가 9.8067m/s²인 다른 천체에만 해당됩니다. 예를 들어, 달은 1.625m/s²의 중력 가속도를 갖고 있어 같은 물체를 1.5m에서 떨어뜨리면 약 1.36초가 더 걸립니다. 영화에서 보던 것과 일치할 것입니다.

이제, 우리의 작업은 땅에 도달하는 데 필요한 시간을 알려주는 일반적인 공식 t(h, g)를 찾는 것입니다. 이는 단순히 높이 h와 중력 가속도 g 값을 가져와 시간 t를 예측하는 모델을 만드는 것에 불과합니다. 나에게 참아주십시오, 친애하는 물리학자분들. 😃

데이터 수집 및 모델 훈련

우주선을 타고 날아다닌 다음 다양한 높이와 행성에서 몇 가지 물건을 떨어뜨렸고, 항상 땅에 도달하는 데 걸리는 시간을 측정했다고 가정해 봅시다. 측정값의 첫 번째 행들은 다음과 같습니다:

높이 (h)	중력 (g)	시간 (t)
10	9.81	1.43
20	9.81	2.01
30	3.72	2.67

이제 이를 훈련 세트와 테스트 세트로 나누어 표준 기계 학습 모델을 훈련시켜 볼 수 있습니다.

import pandas as pd
from sklearn.ensemble import RandomForestRegressor
from sklearn.model_selection import train_test_split

data = pd.read_csv("https://raw.githubusercontent.com/Garve/towards_data_science/main/Symbolic%20Regression/free_fall.csv")
X = data[["h", "g"]]
y = data["t"]
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=123)

rf = RandomForestRegressor(random_state=123).fit(X_train, y_train)
print(rf.score(X_test, y_test))

# 출력:
# 0.9874788707086176

언제든지 궁금한 점이 있으면 물어봐 주세요!

좋아요, 매우 잘 숨겨진 패턴을 학습하는 모델을 만들었네요. 근데... 그 패턴이 뭘까요?

모델 해석

실제로 모델 내부에 존재하는 복잡한 공식 때문에 알아내기 어렵습니다. Shapley 값들을 사용하여 모델이 무엇을 배웠는지 살펴볼 수 있습니다. 이 기사에서는 그들이 무엇인지 정말로 알 필요는 없지만, 여전히 관심이 있다면 제 다른 글을 확인하는 것을 추천합니다:

기본적으로, 다양한 특징이 모델의 결과에 어떤 영향을 미치는지를 결정할 수 있게 해줍니다. 멋진 shap 라이브러리를 사용하여 다음을 할 수 있어요:

# !pip install shap
import shap

te = shap.TreeExplainer(rf, feature_names=["h", "g"])
shapley_values = te(X)
shap.plots.scatter(shap_values=shapley_values)

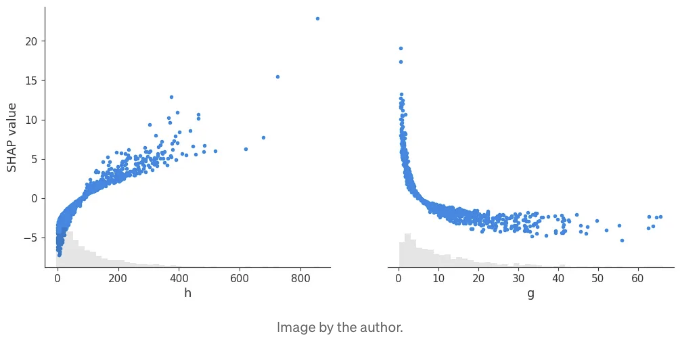
FindHiddenLawsWithinYourDatawithSymbolicRegression_2

왼쪽에서는 높은 h 값이 더 높은 모델 출력, 즉 더 높은 t 값을 초래한다는 것을 볼 수 있습니다. 오른쪽에서는 g 값이 낮을수록 모델에 따르면 더 높은 t 값을 얻는 것을 볼 수 있습니다. 두 관측 결과는 모두 이해하기 쉽습니다: 높은 곳에서 물체를 떨어뜨리면 땅에 닿을 때까지 더 오래 걸립니다. 그리고 지면 쪽으로 강한 힘으로 끌려오게 되면 그것은 더 빨리 땅에 닿을 것입니다.

보통 이러한 결과가 나오면 만족하고 모델을 배포할 수 있습니다. 그럼에도 불구하고, 이 접근 방식에는 몇 가지 문제가 있다고 주장할 수도 있습니다:

모델이 꽤 복잡하므로 이론적 통찰이 전혀 없습니다.
그래서 우리는 scikit-learn 모델로 배포해야 하는데, 우리의 배포 서비스가 scikit-learn 모델을 좋아하지 않을 때 쉽게 다시 구현할 수 없습니다.

이 두 문제를 해결하는 다른 모델을 어떻게 구축할 수 있는지 살펴봅시다.

기호 회귀

기호 회귀라는 기술을 활용할 수 있습니다. 이 기술은 데이터를 설명하는 간단한 대수적 표현을 찾으려고 합니다. 예를 들어, 특성 x₁, x₂ 및 x₃ 및 타겟 y로 구성된 데이터 세트에서 모델 학습 결과는 y = √x₁ + sin(x₂/(x₃+1)) 또는 y = exp(x₁²) - x₂ 와 같을 수 있습니다. "자유 낙하" 데이터 세트에서 이 모델이 어떻게 수행되는지 확인해봅시다.

심볼릭 회귀를 위한 많은 패키지가 있습니다. 예를 들어 gplearn과 PySR이 있어요. 여기서는 gplearn을 사용할 거에요. 살짝 더 쉽게 사용할 수 있어서요. 하지만 안타깝게도 2년 동안 업데이트되지 않았어요. PySR은 활발히 개발 중이지만 밑바닥에는 Julia를 사용하기 때문에 또 다른 종속성이 생기는 거에요.

심볼릭 회귀 맞춤

먼저 gplearn을 설치해볼게요. pip install gplearn을 통해 간단하게 설치할 수 있어요. 그리고 SymbolicRegressor를 정의하고, 덧셈이나 로그 취하기와 같은 연산을 공식 내에서 사용할 수 있도록 설정해보아요.

from gplearn.genetic import SymbolicRegressor

sr = SymbolicRegressor(
    function_set=(
        "add",
        "sub",
        "mul",
        "div",
        "sqrt",
        "log",
        "abs",
        "neg",
    ),
    random_state=0,
)

sr.fit(X_train, y_train)

지금 모델은 다음과 같은 공식을 찾으려고 노력합니다:

간단하면서도
데이터를 잘 설명하는 즉, 손실이 적은 공식

제 경우에는 다음과 같은 결과가 나왔어요:

아래는

Physical laws rediscovered by PySR authors

since x₀ = h and x₁ = g. Apart from having a test r² of over 0.999, this is actually the correct physics formula that describes falling objects without air resistance! You might also find the equivalent formula h = 0.5 · g · t² in literature.

And don’t only take it from me. The authors of PySR published a paper in which they show how many more physical laws could be rediscovered. On page 16, you can see this table:

표 태그를 Markdown 형식으로 변경하세요.

열을 보면 심볼릭 회귀 라이브러리들이 나와 있어요. 왼쪽에는 물리 법칙이 있구요. 셀 안의 분수는 올바른 표현을 찾은 횟수를 전체 시도 횟수로 나눈 것이에요. 다음은 수식들이에요:

Planck의 법칙과 Rydberg 공식은 어떤 라이브러리도 발견하기 어려웠어요. 그래도 PySR만 다른 경우에 잘하고 있었어요. gnlearn은 비교 대상이 아니었어요.

어떻게 이 마법이 작동할까요?

우리 모델의 기능 형태는 완전히 미친 것일 수 있습니다. 이는 신경망에서 일어나는 일과 근본적으로 다릅니다. 신경망에서는 공식 자체가 고정되어 있고 매개변수만 조정됩니다. 또는 그라디언트 부스팅과 같은 트리 기반 알고리즘에서는 결과가 언제나 조각별 상수 함수가 됩니다.

길게 말하면, 이 기사에서 다루기에는 너무 길 것인 내재하는 진화 알고리즘을 사용합니다. 이들은 매우 무작위하고 휴리스틱한 프로세스이며, 극도로 분석하기 어렵습니다. 그래도 실전에서는 상당히 잘 작동할 수 있습니다. 만약 진화 알고리즘에 대해 초보자를 위한 기사를 읽고 싶다면, 제 다른 기사를 확인해 보세요:

지금 읽기 싫다면, 현재 사용 사례에 대한 핵심 아이디어는 여기에 있습니다:

간단한 무작위 수식들로 시작해보세요, 예를 들어 t = h, t = g², t = g + h, t = √h, ...
평가 지표로 예를 들어 평균 제곱 오차를 사용해 그들이 얼마나 좋은지 확인해보세요.
가장 좋은 수식들을 선택하여 결합해보세요, 예를 들어 t = h와 t = g²를 결합하면 t = h + g²가 될 수 있습니다. 또는 t = √h와 t = h · g를 결합하면 t = √(h · g)가 될 수 있습니다.
그들을 변형할 수도 있습니다. 예를 들어, t = √(h·g)를 약간 변경하여 t = √(h + g)로 변형할 수 있습니다.
이제 새로운 수식 집합이 있으므로 다시 1단계로 돌아갈 수 있습니다. 또는 이미 아주 좋은 수식을 찾은 경우 중단할 수도 있습니다.

이러한 절차를 구현하는 방법은 사용하는 라이브러리에 따라 다를 수 있습니다. 이러한 알고리즘을 작성하는 것이 정말 재미있는 일이 될 수 있도록 이러한 단계를 설계하는 데 많은 자유가 주어집니다. PySR 저자들은 논문에서 그들만의 진화 알고리즘 특정 버전을 설명하고 있습니다.

결론

이 글에서는 의미 있는 수식으로 모델을 구축하는 것이 얼마나 쉬운지 살펴보았습니다. 예를 들어, 우리의 예제에서는 테스트 세트의 성능뿐만 아니라, 더 나았습니다.

예를 들어, SQL로 이동하여 다음과 같이 작성할 수 있어요:

SELECT
  h,
  g,
  SQRT(2 * h / g) AS t_pred
FROM
  your_table

그럼 이제 시작해봅시다! 이 공식을 선택하는 어떤 프로그래밍 언어에서도 쉽게 다시 구현할 수 있어요.

물론 공식이 항상 간단하거나 데이터를 잘 설명하지는 않을 수 있어요. 이 경우에는 항상 사인, 지수 함수와 같은 다른 연산을 추가하거나, 자체 작은 빌딩 블록을 만들 수 있어요. 이것은 다시 명확한 공식을 만드는 데 도움이 될 수 있어요.

오늘 새롭고 흥미로운, 가치있는 것을 배우셨기를 바랍니다. 읽어 주셔서 감사합니다!

그리고 알고리즘의 세계로 더 깊이 파고들고 싶다면, 제 새로운 출간물 '알고리즘에 관한 모든 것'을 한 번 살펴보세요! 아직 작가를 모집 중입니다!