이 글을 읽은 후에는 지구 이동 거리(또는 EMD 또는 Wasserstein 거리라고도 함)의 계산 방법에 대해 심층적으로 이해하게 될 것입니다. 이 지식을 통해 다양한 응용 분야에서의 장단점에 대한 좋은 아이디어를 갖게 될 것입니다.
목차
- 지구 이동 거리(EMD)의 정의와 직관
- EMD의 응용
- 처음부터 EMD 계산하기
- scipy 패키지를 사용하여 EMD 계산하기
- 결론
지구 이동 거리의 정의와 직감
지구 이동 거리는 두 분포 간의 차이를 측정하는 특정한 계산 방법입니다. "지구 이동 거리"라는 이름은 직관적인 해석에서 유래했습니다. 다른 위치에 있는 서로 다른 모양의 두 더미의 흙(또는 토얄)이 있다고 상상해보세요. EMD는 두 번째 더미를 첫 번째 더미처럼 보이도록 옮기는 데 필요한 작업량(총 토얄량 times 거리로 정의됨)을 의미합니다.
이를 예시로 가장 잘 설명할 수 있다고 생각합니다: A와 B 두 분포가 있다고 가정해보겠습니다. 우리가 궁금한 것은 두 분포가 얼마나 다른지 입니다. EMD는 A를 B로 변환하고 변환을 완료하는 데 필요한 총 작업량(즉, 이동한 단위 수 X 이동 거리)을 측정하여 이 질문에 대답합니다. 아래 예시는 두 간단한 분포의 EMD를 계산하는 방법을 설명합니다:
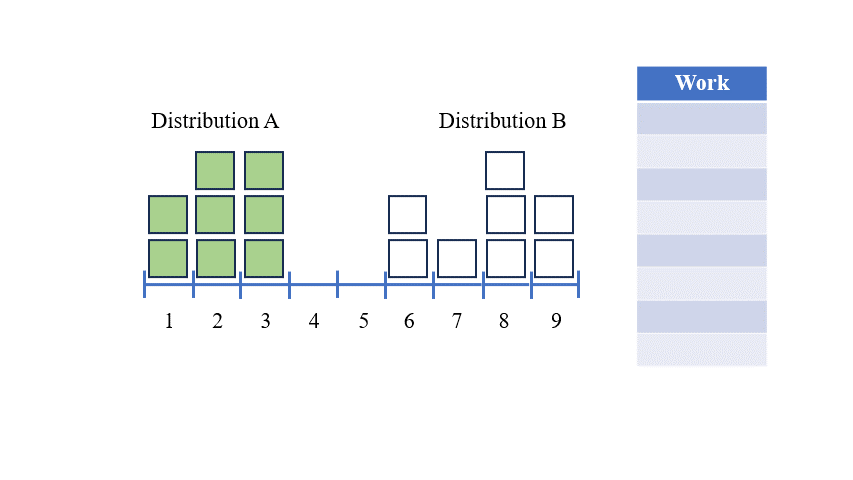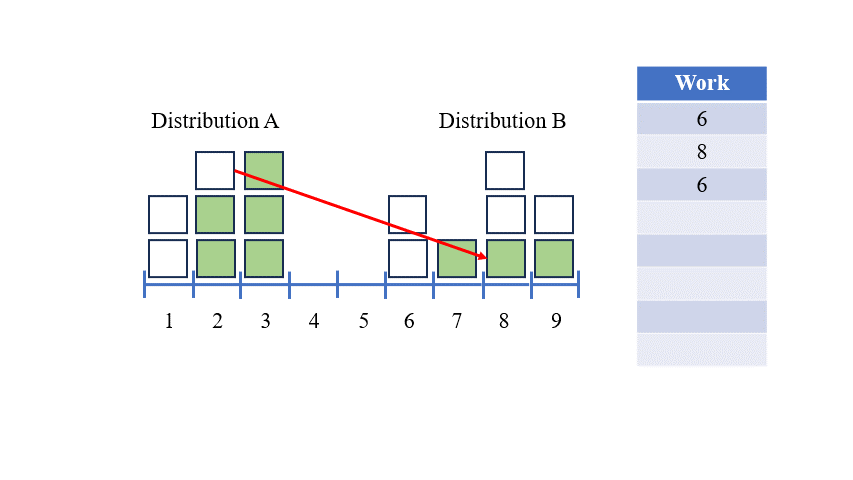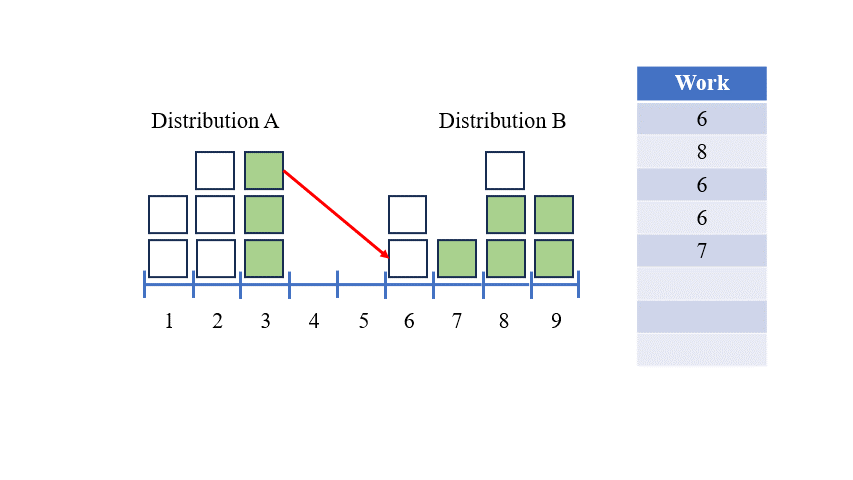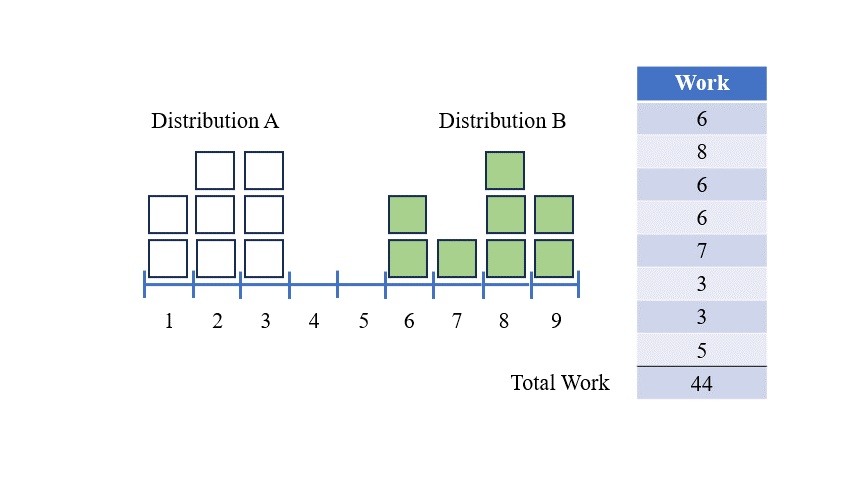
한 분포를 다른 분포로 변환하기 위해 우리가 하는 움직임 집합을 '운송 계획'이라고 합니다 — 한 위치에서 물질이나 물품을 다른 위치로 운반하는 것을 상상해보세요.
위의 그래픽에 대한 운송 계획은 다음과 같습니다:
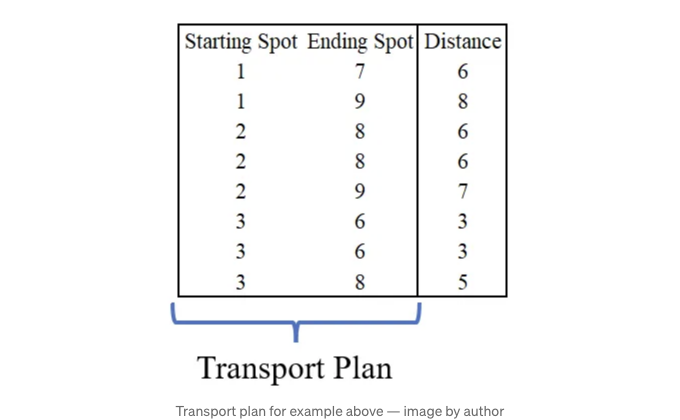
이 운송 계획은 우리에게 분포 A를 분포 B로 가장 효율적으로 변환하는 방법을 보여줍니다. 이 운송 계획의 총 작업량이 두 분포 간의 EMD입니다.
지구 이동자 거리의 응용
지구 이동자 거리는 물론 거리의 한 종류입니다! 따라서 그 응용 분야는 일반적으로 비교 중심입니다. 이 글에서는 지구 이동자 거리의 세 가지 응용을 살펴볼 텐데요. 지구 이동자 거리가 어떻게 유용하게 사용될 수 있는지 감을 잡을 수 있게 도와줄 거예요.
지구 이동자 거리는 기계 학습에서 모델 모니터링에 사용될 수 있습니다. 모델 모니터링에서 데이터 과학자들은 모델 입력과 출력이 시간이 지남에 따라 어떻게 변화하는 지 관찰합니다. 지구 이동자 거리는 훈련 데이터셋과 프로덕션 데이터셋 간의 차이를 정량화하여 입력 또는 출력 변화를 정량화하는 데 사용될 수 있습니다. 큰 지구 이동자 거리 값은 모델을 수정하거나 재훈련해야 할 수도 있다는 것을 시사할 수 있습니다.
지구 이동자 거리는 또한 이미지 비교/검색에 사용됩니다. 두 이미지 사이의 픽셀 분포를 비교하여 이들의 유사성을 계산할 수 있습니다. 이 유사성을 사용하여 이미지들이 얼마나 비슷한 지 비교나 검색에 활용할 수 있습니다.
EMD는 문서를 비교하는 데 사용될 수 있습니다. 다양한 ETL 측정치 간의 분포를 비교하여 문서가 유사한지 확인할 수 있습니다. 이 애플리케이션을 사용하여 원본이어야 하는 문서가 다른 문서들과 유의한 유사성을 가지고 있는지 확인하여 표절을 식별할 수 있습니다.
물론 이는 EMD의 응용 프로그램의 전체 목록은 아니지만, EMD가 실제로 어떻게 사용될 수 있는지에 대한 아이디어를 제공할 수 있기를 희망합니다.
빈손에서 Earth Mover's Distance 계산하기
EMD의 해석은 간단하고 직관적이지만, 계산은 다소 복잡합니다. 빈손에서 계산하는 것이 효과적인 학습 전략이라고 생각돼서 여기서 그렇게 할 것입니다! 이 섹션을 마치면 정확히 어떻게 Earth Mover's Distance가 계산되는지 이해하게 될 거예요!
최적화
EMD(지구 이동자 거리)의 정의 중 하나인 중요한 부분 중 하나는 지금까지 간과했던 사항으로, EMD는 가장 효율적인 운송 계획에 필요한 최소 작업량입니다. 최적화는 계산의 핵심입니다! 우리는 최적화를 실행하여 최상의 운송 계획을 찾고, 그 솔루션에 해당하는 작업량을 계산해야 합니다. 그 작업량이 바로 EMD입니다!
만약 두 분포가 n개의 관찰을 가지고 있다고 가정하면 (몇 가지 예외 상황에 대해 조금 후에 논의하겠습니다), n!개의 고유한 운송 계획이 있습니다. 계승에 익숙하지 않다면, 계승은 신속하게, 정말 빨리 증가합니다. 예를 들어, 위 섹션에서의 소규모 예제의 경우, 크기가 8인 두 분포가 있습니다. 모두 8! = 40,320개의 고유한 운송 계획이 있습니다! 이는 그러한 소규모 분포에 대해 매우 많은 양이며, 분포 크기가 커질수록 빠르게 처리할 수 없게 됩니다.
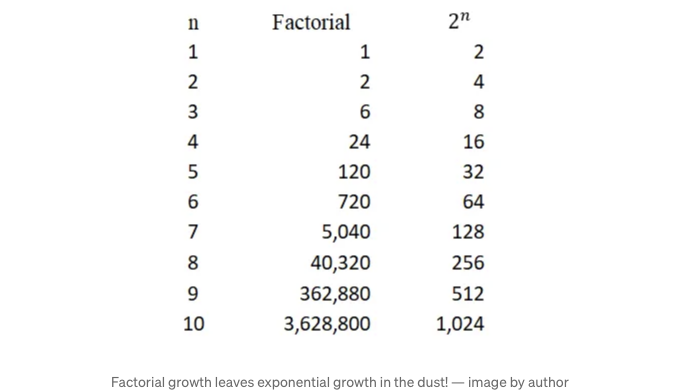
팩토리얼로 커지는 해결 공간 때문에 매우 작은 문제조차 가장 효율적인 운송 계획을 찾기 위한 모든 잠재적인 해결책을 살펴볼 수는 없어요. 다행히 EMD 운송 문제는 선형 프로그래밍 최적화 문제로 인코딩할 수 있어요. 선형 프로그래밍이 사용하는 '트릭' 덕분에 모든 잠재적인 해결책을 탐색하지 않고도 전역 최적해를 찾을 수 있어요.
이제 EMD 운송 문제를 선형 프로그래밍 문제로 설정하는 방법에 대해 알아볼게요. 모든 최적화 문제에는 목표와 제약 조건이 있어요 - 아래에서 선형 프로그래밍 EMD 문제의 목표와 제약 조건을 살펴볼게요.
목표:
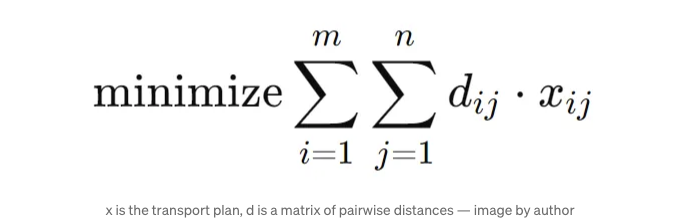
제약 사항:
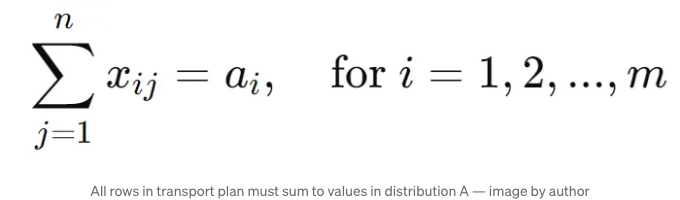
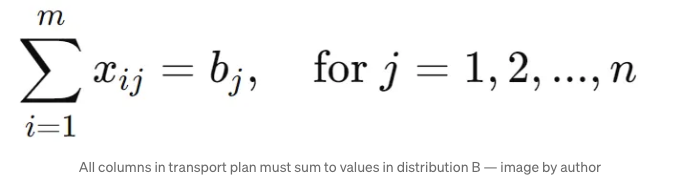
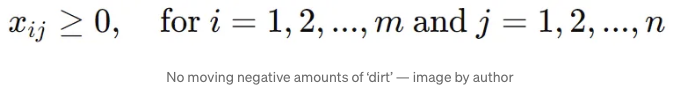
이 최적화 구성 요소를 자세히 살펴봐요. 최적화 구성 요소를 살펴보면서, 예시로 두 개의 간단한 분포를 사용할 거에요. 이 분포들은 각각 3개의 관측값을 가지고 있어요: 분포 A = [1, 2, 3] 그리고 분포 B = [5, 6, 7].
목적 함수
가장 먼저 목적 함수에 대해 이야기해봐요. 목적 함수에는 두 부분, 즉 전송 계획 xᵢⱼ와 비용 행렬 dᵢⱼ이 포함되어 있어요.
이전 섹션에서 긴 형식의 전송 계획을 보여줬어요. 선형 프로그래밍 최적화를 위해, 해당 전송 계획을 분포 A 값을 열로, 분포 B 값을 행으로 가지는 행렬로 이동할 거예요. 최적화 과정은 최적의 전송 계획을 생성해내요. 전송 계획은 두 분포 간의 관측값 조합마다 값을 가지고 있어요.
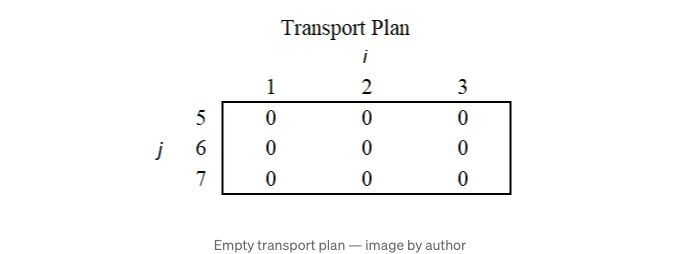
Cost matrix인 dᵢⱼ는 이동 계획의 각 셀에 관련된 작업량을 매핑합니다.

최적화 함수는 이동 계획과 비용 행렬의 내적을 취하여 특정 이동 계획에 대한 총 작업량을 계산합니다. 최적화 프로세스는 작업을 최소화하는 이동 계획을 찾습니다. 이 최소 작업량이 지구 이동자 거리입니다.
이제 운송 계획이 포함된 상태에서 해당 비용 행렬을 통해 총 작업량이 어떻게 계산되는지 살펴봅시다.
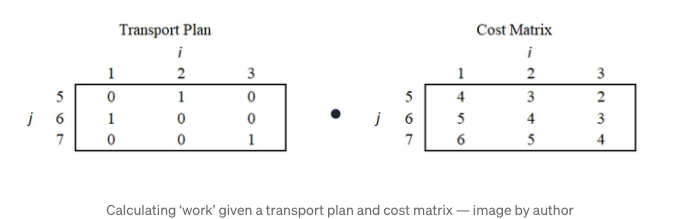
위의 행렬에 대한 점곱은 다음과 같이 계산됩니다:
총 작업량 = (04) + (15) + (06) + (13) + (04) + (05) + (02) + (03) + (1*4)
총 작업량 = (15) + (13) + (1*4) = 12
우리의 목적 함수는 운송 계획과 비용 행렬의 내적을 최소화하려는 것입니다.
규칙
규칙은 조금 복잡해 보일 수 있지만 실제로는 매우 직관적입니다. 첫 번째 규칙은 각 관찰이 운송 계획에 포함되도록 하는 것입니다. 즉, 이 규칙은 첫 번째 분포의 각 관찰이 두 번째 분포로 딱 한 번 이동되도록 합니다. 두 번째 규칙은 최종 '변환된' 분포가 두 번째 분포와 일치하도록 하는 것을 보장합니다. 마지막 규칙은 최적화가 음의 수량을 이동하려고 시도하지 않도록 하여 이치에 맞지 않게 하는 것을 방지합니다.
아래는 세 가지의 무효한 운송 계획과 하나의 유효한 계획이 있습니다. 이 중 몇 가지를 살펴보고 제약 조건이 어떻게 비현실적인 운송 계획을 막는지 이해해 보겠습니다.
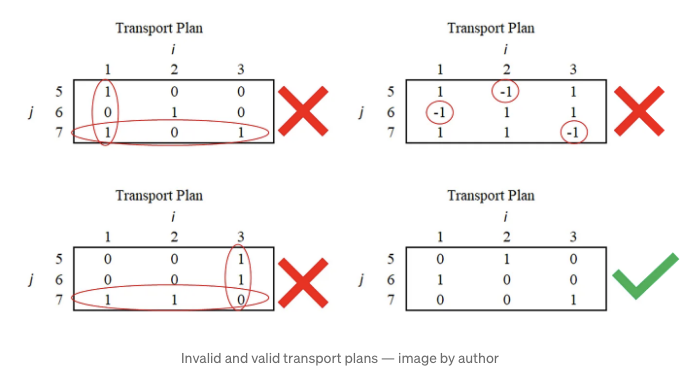
왼쪽 상단: 위치 1에서 단위 하나가 위치 5로 이동하고 단위 하나가 위치 7로 이동합니다. 이는 위치 1에 단위 하나만 있는데 두 곳으로 한 단위를 이동시키는 것은 위배 사항입니다! 따라서 한 단위를 두 곳으로 이동시키는 것은 불가능합니다. 첫 번째 제약은 이런 일이 일어나지 않도록 합니다.
위치 2에 있는 단위 하나가 위치 6으로 이동하는 것에는 문제가 없습니다.
위치 3의 한 단위가 위치 7로 이동합니다. 이것은 또한 위반입니다. 왜냐하면 위치 7로 두 단위가 이동한다면 (위치 1에서의 한 단위와 위치 3에서의 한 단위), 우리가 A를 변환하는 배포는 B 배포와 같지 않습니다 (B는 위치 7에 단위 하나만 있는데 반해). 이 문제는 두 번째 제약으로 방지됩니다.
오른쪽 상단: 오른쪽 상단 솔루션은 전혀 논리적인 의미가 없습니다. 어떻게 음수 단위를 이동할 수 있을까요? 그러나 이 계획은 첫 번째 두 제약을 모두 위반하지 않음을 주목하세요! 모든 행과 열이 해당 단위의 총합과 일치합니다 (이 예제에서 합은 1입니다). 기계는 이것이 비논리적임을 모르죠. 이런 종류의 헛소리 솔루션을 방지하기 위해 다음과 같은 세 번째 제약을 포함해야 합니다. 다른 두 제약은 이것을 잡아내지 못합니다!
다른 두 운송 계획 해석은 독자에게 맡기겠습니다 (특히 왜 오른쪽 하단 계획이 유효한지).
관찰 수가 다른 배포
지금까지는 두 분포가 관찰치의 수가 동일한 단순한 예제만 살펴보았습니다. 이렇게 하면 사소합니다. 왜냐하면 일대일 매핑이 작동하기 때문입니다(A 분포에서 한 관찰치가 B 분포의 한 위치로 이동합니다). 그러나 이것은 특수한 경우입니다. EMD의 많은 응용에서 분포의 크기가 다를 수 있습니다. 이런 경우에는 우리가 설정한대로 최적화가 작동하지 않을 것입니다!
다행히도 수정하는 것은 그렇게 어렵지 않습니다. 최적화의 프레임워크(목적 함수와 제약 조건)는 사용 가능합니다—우리는 최적화를 실행하기 전에 몇 가지 수정을 해야 합니다.
최적화에 숫자의 원시 목록을 입력하는 대신에 확률 분포를 입력합니다. 확률 분포는 관측치들의 개별 비율을 가지는 분포를 의미합니다.
예를 들어, [1, 1, 2, 2, 2, 3, 3, 3] 분포가 있다고 가정해 봅시다. 이를 확률 분포로 변환하기 위해, 먼저 각 고유값의 개수를 얻습니다—이 경우 [2, 3, 3] (1이 두 개, 2가 세 개, 3이 세 개 있다). 확률 밀도는 항상 하나로 합쳐집니다(이 특성 덕분에 다른 크기의 분포를 비교할 수 있습니다)—우리의 빈도 수가 하나로 합치려면, 모든 빈도수의 합으로 각 빈도를 나누기만 하면 됩니다—[2/8, 3/8, 3/8] = [0.25, 0.375, 0.375]. 이제 우리의 분포가 변환되었으니 EMD 계산에 직접 입력할 준비가 되었습니다.
확률 분포에서 원시 분포로의 변환 후에는 관측치의 위치를 잃게 됩니다. 예를 들어, 0.25가 위치 1에 해당한다는 것을 알 수 없습니다. 이것이 거리 행렬이 필요한 이유입니다. 거리 행렬은 변환되지 않으며 최적화 프로세스에서 사용할 상대적인 위치 간 거리를 보존합니다. EMD의 정의도 약간 바뀝니다. 확률 분포로의 변환으로 인해 최소 작업에서 단위당 평균 최소 작업으로 변경됩니다.
코딩
설정을 이해했으니, 수동 계산을 위한 코딩을 진행해 보겠습니다. 선형 프로그래밍 최적화를 수행하기 위해 pulp 패키지를 사용할 것입니다.
EMD를 수동으로 계산하는 코드는 다음과 같습니다:
import numpy as np
import pandas as pd
from scipy.stats import wasserstein_distance
import pulp
# 선형 프로그래밍을 사용하여 수동으로 emd 계산
def emd_manual(a, b):
'''
임의 크기의 두 분포가 주어졌을 때 EMD를 계산합니다
입력:
a (list) : 첫 번째 분포에 대한 관측치 목록
b (list) : 두 번째 분포에 대한 관측치 목록
출력:
emd_calc (float) : EMD 계산값
transport_plan (dict) : transport plan의 행/열이 키이며
해당 요소는 해당 위치로 이동하는 관측치 수입니다
'''
# 각 고유 값의 발생 횟수 계산
a_unique, a_counts = np.unique(a, return_counts=True)
b_unique, b_counts = np.unique(b, return_counts=True)
# 확률 분포로 변환
prob_dist_a = a_counts / np.sum(a)
prob_dist_b = b_counts / np.sum(b)
norm_a = prob_dist_a / np.sum(prob_dist_a)
norm_b = prob_dist_b / np.sum(prob_dist_b)
# 확률 분포의 크기 가져오기
n = len(norm_a)
m = len(norm_b)
# pulp 선형 프로그래밍 문제 설정
emd_problem = pulp.LpProblem('EMD', sense=1)
# 결정 변수 정의
x = pulp.LpVariable.dicts("x", [(i, j) for i in range(n) for j in range(m)],
lowBound=0, cat='Continuous')
# 목적 함수 추가 (총 비용 최소화)
emd_problem += pulp.lpSum(x[i, j] * np.abs(a[i] - b[j])
for i in range(n) for j in range(m))
# 제약 조건 1
for i in range(n):
emd_problem += pulp.lpSum(x[i, j] for j in range(m)) == norm_a[i]
# 제약 조건 2
for j in range(m):
emd_problem += pulp.lpSum(x[i, j] for i in range(n)) == norm_b[j]
# 제약 조건 3
for i in range(n):
for j in range(m):
emd_problem += x[i, j] >= 0
# 문제 풀이
emd_problem.solve()
if emd_problem.status == 1:
print('해결책 찾음!')
else:
print('가능한 해결책 없음')
# 해결에서 emd 계산
emd_calc = pulp.value(emd_problem.objective)
# transport plan 조합
transport_plan = {(i, j): pulp.value(x[i, j]) for i in range(n) for j in range(m)}
# 정규화를 위한 transport plan 조정
for key in transport_plan:
transport_plan[key] *= len(a)
transport_plan[key] = round(transport_plan[key])
return emd_calc, transport_plan
# 테스트 분포로 emd_manual 함수 실행
if __name__ == "__main__":
a = [1, 1, 2, 2, 2, 3, 3, 3]
b = [6, 6, 7, 8, 8, 8, 9, 9]
emd, transport_plan = emd_manual(a, b)
print(emd)
print(transport_plan)
Scipy를 사용하여 EMD 계산
물론, EMD를 계산할 때마다 이러한 코드를 작성하는 것은 아주 미친 짓일 것입니다. 한 번만 작성하고 재사용해도, 잘 검증된 Python 패키지의 함수만큼 견고하고 효율적일 수 없을테니요. 저는 순수 코드를 학술적인 연습으로 썼을 뿐입니다! 다행히도, 대부분의 일반적인 계산과 마찬가지로 이미 이를 위해 설치 가능한 패키지가 있습니다! scipy 패키지에는 stats 모듈 내의 wassertein_distance 함수가 있습니다. 아래 코드에서 볼 수 있듯이 사용하기 매우 쉽습니다!
from scipy.stats import wasserstein_distance
if __name__ == '__main__':
a = [1, 1, 2, 2, 2, 3, 3, 3]
b = [6, 6, 7, 8, 8, 8, 9, 9]
emd = wasserstein_distance(a, b)
print(emd)
이 함수를 사용하여 손 계산 결과가 내장 계산 결과와 동일한지 확인할 수 있습니다.
결론
어스 이동 거리(Earth Mover's Distance)는 두 분포 간의 차이를 이해하는 데 도움이 되는 계산 방법입니다. 이는 두 분포를 서로 비교해야 하는 여러 응용 프로그램에서 유용합니다.
자체적 계산은 첫 번째 분포를 두 번째로 변환하는 데 필요한 최소한의 총 이동량입니다. 최소한의 양을 찾고 있기 때문에 선형 프로그래밍을 활용하여 최적화를 수행합니다. 이를 파이썬으로 수동으로 계산할 수는 있지만 pulp 패키지를 사용하는 것은 그다지 실용적이지 않습니다. EMD는 scipy 패키지의 stats 모듈 내 wasserstein_distance 함수를 사용하여 쉽게 계산할 수 있습니다.
깃허브 링크: https://github.com/jaromhulet/emd_manual_calculations