
약물 발견에서 종 분류, 신용 점수 매기기, 사이버 보안 등 랜덤 포레스트는 복잡한 세상을 모델링하는 인기 있고 강력한 알고리즘입니다. 그 다양성과 예측 능력은 첨단 복잡성을 필요로 할 것 같지만, 랜덤 포레스트가 실제로 무엇인지 파헤쳐보면 놀랍게 간단한 일련의 반복 단계들로 이뤄져 있습니다.
저는 무엇인가를 배우는 가장 좋은 방법은 그것과 놀아보는 것이라고 생각합니다. 그러므로 랜덤 포레스트가 어떻게 작동하는지 직관을 얻기 위해 Python으로 직접 포레스트를 만들어 봅시다. 의사 결정 트리에서 시작하여 완전한 포레스트로 확장해보겠습니다. 우리는 분류와 회귀 모두에 대해 이 알고리즘이 얼마나 유연하고 해석 가능한지 직접 확인할 것입니다. 이 프로젝트가 복잡해 들리더라도 실제로 우리가 배워야 할 핵심 개념은 1) 데이터를 순차적으로 분할하는 방법, 2) 데이터가 얼마나 잘 분할되었는지를 어떻게 정량화 하는가 입니다.
배경
의사 결정 트리 추론
의사 결정 트리는 피처를 레이블과 매핑하는 이진 규칙 집합을 식별하는 지도 학습 알고리즘입니다. 로지스틱 회귀와 같은 알고리즘과 달리 출력이 방정식인 것이 아니라 의사 결정 트리 알고리즘은 비모수적이므로 피처와 레이블 간의 관계에 강한 가정을 하지 않습니다. 이는 의사 결정 트리가 훈련 데이터를 최적으로 분할하는 방식으로 자유롭게 성장할 수 있기 때문에 결과적인 구조가 데이터 집합에 따라 다양하다는 것을 의미합니다.
의사 결정 트리의 주요 장점 중 하나는 해석 가능성입니다. 분류를 위해 카테고리를 예측하는 트리가나 회귀를 위해 연속 값을 예측하는 각 단계는 트리 노드에서 확인할 수 있습니다. 예를 들어, 온라인에서 본 제품을 구매할지 예측하는 모델은 다음과 같이 보일 수 있습니다.
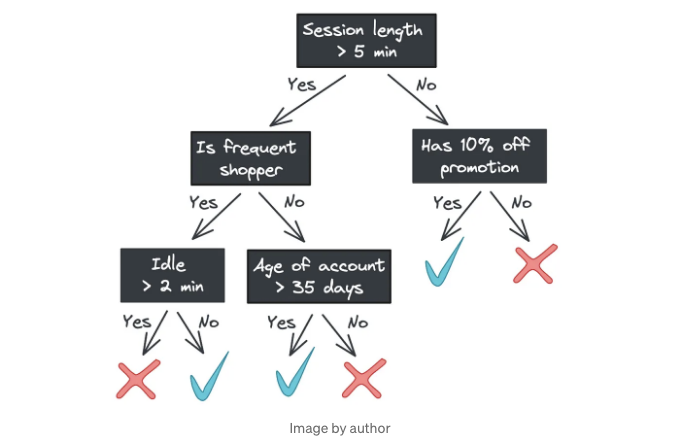
루트부터 시작하여, 트리의 각 노드는 이진 질문을 하며 (예: "세션 길이가 5분보다 길었습니까?"), 답변에 따라 피처 벡터를 두 개의 자식 노드 중 하나로 전달합니다. 자식 노드가 없는 경우 - 즉, 리프 노드에 도달한 경우 - 트리는 응답을 반환합니다.
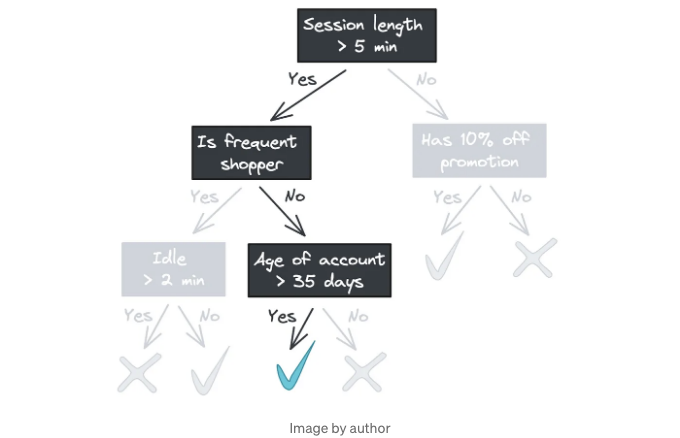
(이 블로그 포스트에서는 분류에 초점을 맞추겠지만, 의사 결정 트리 회귀기는 순차적 값이 아닌 클래스 레이블이 아닌 연속 값을 반환하게 됩니다.)
의사 결정 트리 학습
유추 또는 이 예측 프로세스는 꽤 간단합니다. 그러나 이 트리를 구축하는 것은 훨씬 명백하지 않습니다. 각 노드의 이진 규칙은 어떻게 결정되는 걸까요? 트리에 사용되는 특성들은 무엇이며, 어떤 순서로 사용되는 걸까요? 0.5 또는 1과 같은 임계값은 어떻게 결정되는 걸까요?
의사 결정 트리가 어떻게 구축되는지 이해하기 위해, 우리가 모양(사각형과 삼각형)의 대형 데이터 세트를 특징에 기반하여 사각형만 또는 삼각형만 포함하는 작은 데이터 세트로 분할하려고 한다고 상상해 봅시다. 이상적인 경우에는 모양을 완벽하게 분리하는 몇몇 범주형 특성이 있습니다.
하지만 항상 그렇게 간단하지는 않습니다. 행운이 따르면, 대신 모양을 완벽하게 분리하는 어떤 임계값을 가진 연속적인 특성이 있을 수도 있습니다. 정확한 임계값을 찾기 위해 몇 번의 시도가 필요하지만, 그런 다음 완벽한 분할이 이루어집니다. (휴!)
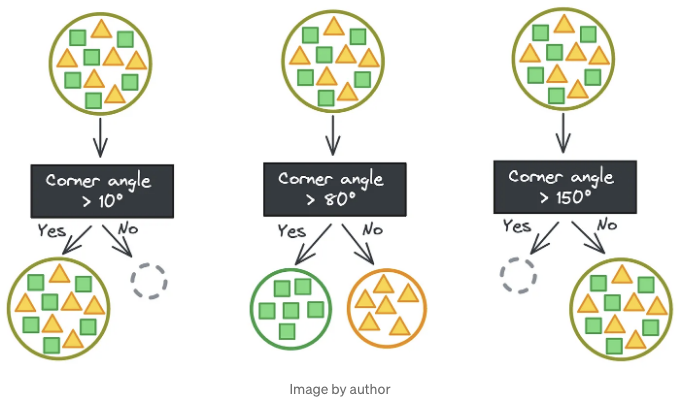
그렇게 간단하지는 않죠. 이 장난감 예제에서는 모든 삼각형과 사각형이 동일하기 때문에 그들의 특성 벡터를 분리하는 것이 쉬워요. (하나의 삼각형에 대해 작동하는 규칙이 모든 삼각형에 적용됩니다!)
하지만 실제 세상에서는 특성이 레이블로 깔끔하게 매핑되지 않습니다. 전자 상거래 예제로 돌아가서, 세션에서 사이트에 보낸 시간과 같은 특성은 어떤 임계값에서도 클래스를 완벽하게 분할하지 못할 수도 있어요.
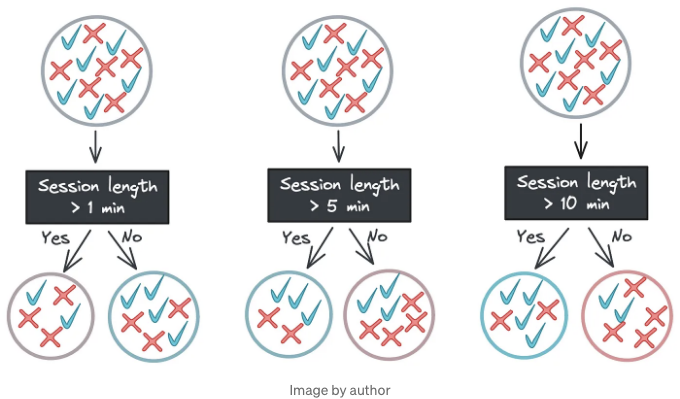
만약 어떤 임계값에서도 데이터를 완벽하게 분리할 수 있는 특성이 없다면 어떻게 해야 할까요? 이 경우, 레이블 집합이 얼마나 "혼합된"지를 측정하는 방법이 필요합니다. 일반적으로 사용하는 지표 중 하나가 지니 불순도인데, 다음 식으로 계산됩니다:
Gini = 1 - Σ(pk)^2
여기서 pk는 우리의 m개 클래스 중 하나에 속할 확률입니다. 제곱과 1의 합이 1이 되어야 하므로, 두 가지 클래스인 사각형과 삼각형의 경우, 이 식을 pk로 정의할 수 있습니다.
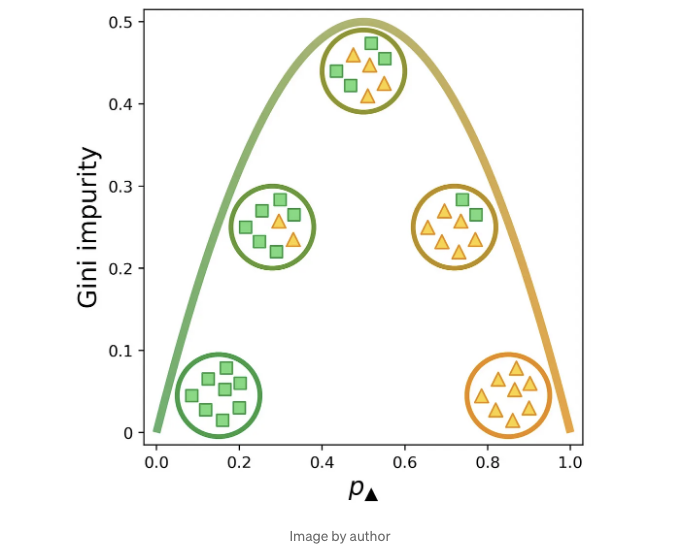
아래는 p✓, 집합에서 양성 레이블을 무작위로 선택할 확률에 따른 지니 불순도의 시각적 표현입니다. [1] (우리는 pk를 p✓로 대체하여 확인 표지가 양성 클래스임을 나타냈습니다.) 집합의 요소가 모두 확인 표지가 아닌 경우(즉, x인 경우) 또는 모두 확인 표지인 경우에 지니 불순도가 가장 낮습니다. 지니 불순도는 x와 확인 표지가 같은 수 일 때 최대치에 도달합니다.
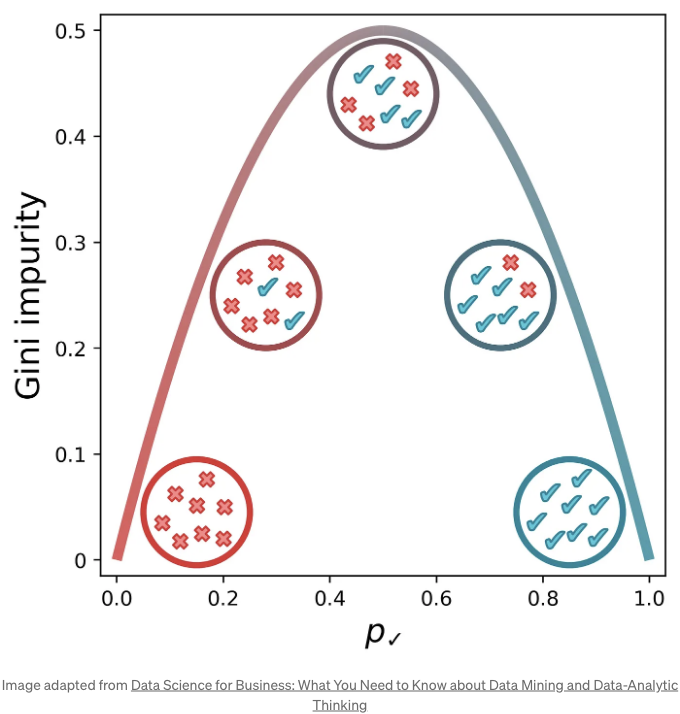
그렇기 때문에 클래스를 분할하기 위해 규칙을 식별할 때, 우리는 단순히 각 하위 집합의 가중치를 고려해 지니 불순도를 최소화하는 분할을 선택할 수 있습니다. (각 하위 집합은 고유의 불순도를 가지고 있으므로 각 하위 집합의 샘플 수로 가중 평균을 취합니다.) 주어진 특성에 대해, 해당 특성의 모든 가능한 값으로 데이터를 분할하고, 하위 집합의 가중치가 적용된 지니 불순도를 기록한 다음, 가장 낮은 불순도를 초래한 특성 값을 선택할 수 있습니다.
아래에서, 계정 연령 특성을 35일을 기준으로 분할하면, 제품을 구매하는 사용자와 구매하지 않는 사용자를 가장 잘 분리할 수 있습니다 (상상의 데이터셋에서).
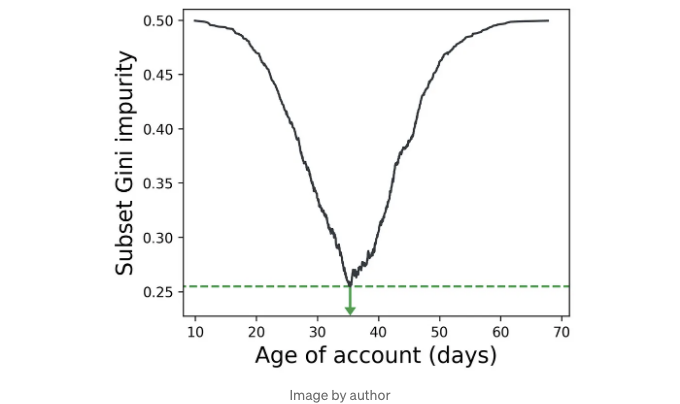
우리는 모든 특성에 대해 이 과정을 반복하고, 최적 분할 결과 지니 불순도가 가장 낮은 특성을 선택할 수 있습니다. 아래에서 세션 길이의 최적 분할이 계정 연령과 빈번한 쇼핑객에 대한 최적 분할보다 낮은 지니 불순도를 보여줍니다. 빈번한 쇼핑객은 이진 특성이므로 분할할 값이 하나뿐입니다.
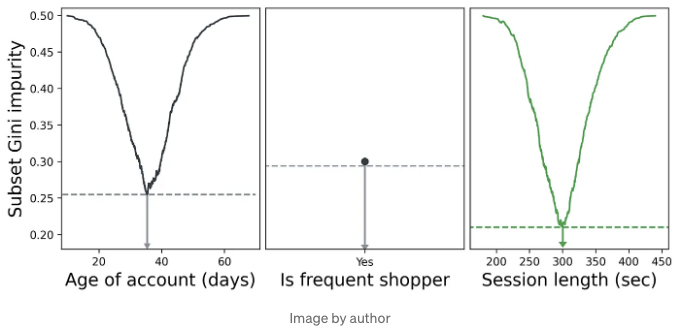
세션 길이에 대한 분할 5분이 우리 결정 트리에서 첫 번째 분기가 됩니다. 그런 다음 특성 및 값 반복 프로세스를 반복하고 각 부분집합, 그들의 하위 부분집합 등에 대해 데이터를 최적으로 분할하는 최상의 특성을 선택합니다. 이렇게 완벽하게 분할된 데이터가 필요하거나 트리가 허용된 최대 깊이에 도달할 때까지 진행합니다. (다음 섹션에서 자세히 설명하겠습니다.)
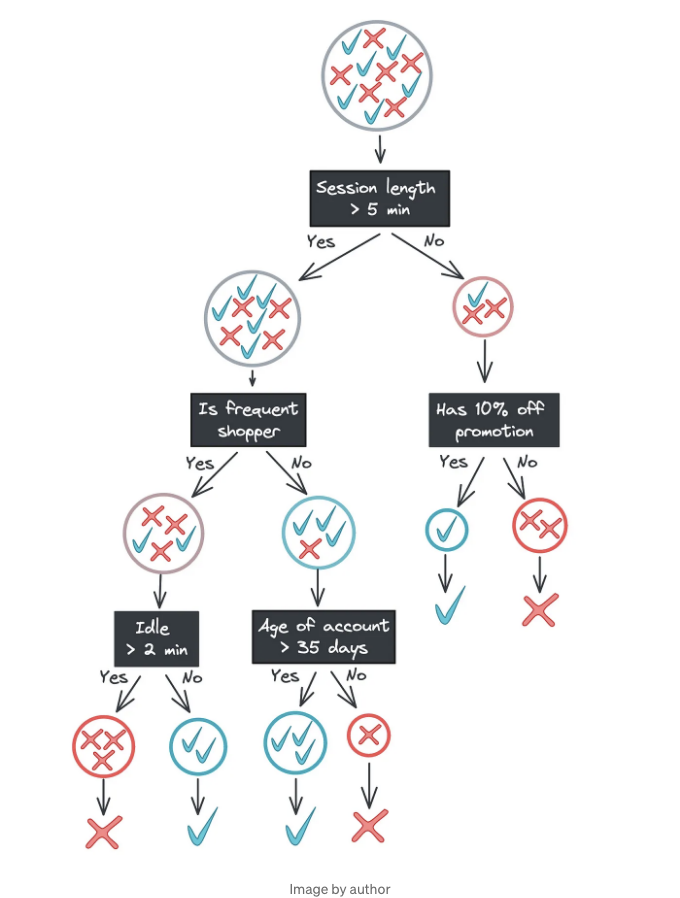
여기에 앞서 본 트리가 나타난 것이지만 각 노드에 훈련 데이터가 표시되어 있습니다. 트리를 아래로 이동할수록 양성 및 음성 클래스가 점점 분리되는 것을 주목하세요. 트리의 맨 아래에 도달하면 잎 노드는 데이터 하위 집합에서의 과반 클래스를 출력합니다. (우리의 경우에는 유일한 클래스입니다.)
랜덤 포레스트
위의 결정 트리는 데이터를 하나의 클래스 레이블만 포함하도록 분할합니다 (즉, Gini 불순도 = 0). 이렇게 함으로써 모델이 훈련 데이터를 설명하는 능력을 최대화하지만, 모델을 데이터에 과적합할 위험이 있습니다. 모델이 모든 특징-레이블 조합을 외우는 것이 아니라 근본적인 패턴을 학습하는 대신에 기억하는 것처럼 생각해보세요. 과적합된 모델은 일반화하기 어렵고, 일반적으로 모델링의 목표인 새로운 데이터에 대한 일반화가 어려워집니다.
과적합을 방지하는 몇 가지 방법이 있습니다. 한 가지 방법은 트리의 깊이를 제한하는 것입니다. 예를 들어 위의 트리를 두 레벨로 제한하면 왼쪽 가지를 자주 쇼핑 고객 분할에서 끝낼 수 있습니다.
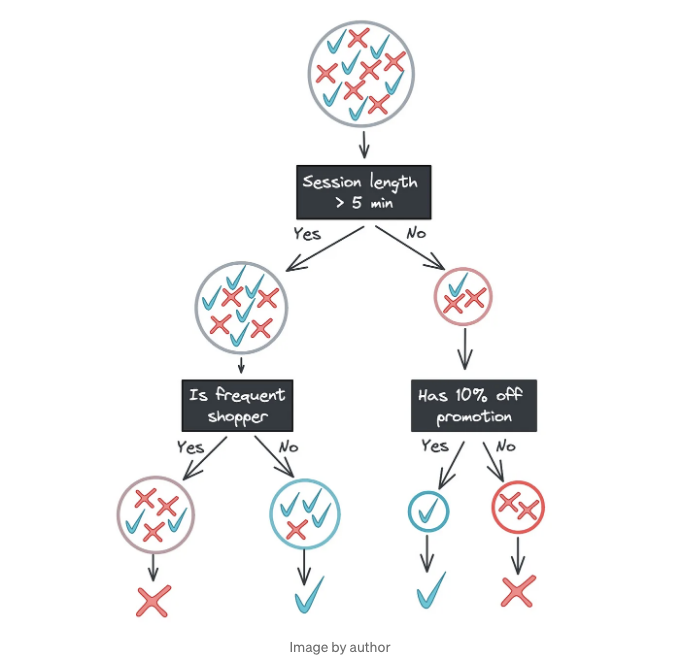
이제 왼쪽 가지의 잎 노드에는 자신들의 하위 집합에서 혼합된 레이블이 있습니다. 이 "불순도"를 허용하는 것은 비최적적으로 보일 수 있지만, 이는 잡음이 있는 피쳐에 대한 강력한 방어 수단입니다. 예를 들어, 훈련 데이터에서 Time idle과 Age of account가 우연히 예측력이 있었다면, 해당 피쳐를 제외한 모델이 새 데이터에 대해 일반화하는 데 더 좋을 것입니다.
트리 깊이 제한은 효과적입니다. 하지만 더 강력한 전략과 함께 사용할 수 있습니다: 앙상블 학습. 머신러닝에서 - 그리고 동물 집단에서도 - 일련의 예측을 집계하면 종종 개별 예측보다 더 높은 정확도를 달성할 수 있습니다. 개별 모델의 오류가 상쇄되어 모델링되는 데이터의 기본 패턴을 더 명확하게 볼 수 있습니다.
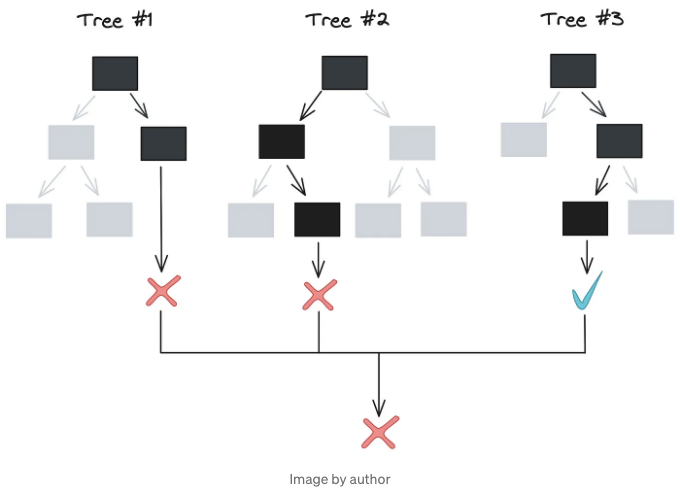
이거 굉장히 좋은데, 전체 모델 예측에 변동이 있어야 앙상블이 유용해집니다. 지난 섹션에서 설명한 알고리즘 - 모든 피처의 모든 값에 대해 Gini 불순도가 가장 낮은 지점에서 분할 - 은 결정론적입니다. 주어진 데이터 세트에 대해 저희 알고리즘은 항상 동일한 의사결정 나무 [2]를 출력하므로, 앙상블로 10개 또는 100개의 트리를 학습시켜도 실제로 아무것도 이루지 못할 것입니다. 그렇다면 왜 숲이 단일 트리보다 나은가요?
여기서 랜덤성이 등장합니다. 랜덤 포레스트 내의 트리들 사이에는 데이터 분할 방식 및 데이터 자체의 변화가 있어서 모델 예측에 변동이 생기고, 오버피팅에 대한 더 큰 방어 기능을 제공합니다.
우선 데이터로 시작해보죠. 부스트랩을 사용하여 데이터를 샘플링하거나 대체로써 모델에 영향을 미치는 아웃라이어들이 무의미한 상관 관계를 가로채는 것을 방지할 수 있습니다. 아이디어는 아웃라이어가 희박하기 때문에 실제 피처와 레이블 간의 진짜 관계를 반영하는 샘플보다 덜 무작위로 선택될 가능성이 높다는 것입니다. 부스트랩을 사용하면 숲 내의 각 의사결정 트리에 약간 다른 데이터 세트를 제공할 수 있어서 여전히 동일한 일반적인 경향을 포함할 것입니다.
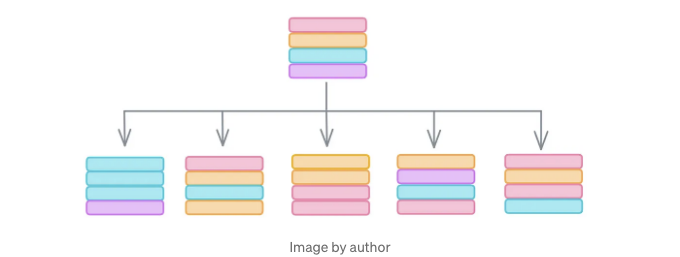
두 번째 방법은 랜덤 포레스트가 데이터를 분할할 때 일부 기능의 임계값을 찾을 때 무작위로 기능의 서브셋만 선택한다는 것입니다. 예를 들어, scikit-learn의 RandomForestClassifier는 지니 불순도를 최소화하는 임계값을 찾을 때 기능 수의 제곱근만 고려합니다.
이 방법들은 이상하게 보일 수 있습니다. 왜 우리가 모든 기능을 사용하지 않는 걸까요? 그리고 왜 의도적으로 데이터에서 행을 중복하거나 삭제할까요? 실제로, 이 방식으로 생성하는 각 개별 트리는 종종 보통의 결정 트리보다 예측 능력이 상당히 떨어집니다. 그러나 수십 개의 이러한 Swiss-cheese 트리를 집계하면 놀라운 결과가 나타납니다: 원래의 결정 트리보다 더 정확한 랜덤 포레스트가 형성됩니다.

구현
이제 직접 Python에서 랜덤 포레스트를 구현해 봅시다. 트리의 노드부터 시작해서 의사 결정 트리, 마지막으로 랜덤 포레스트까지 구현해 보겠습니다.
노드
먼저, 의사 결정 트리에서 노드 역할을 하는 클래스를 만들어 봅시다. 이 클래스는 훈련에 사용되는 다음과 같은 속성을 가지고 있을 것입니다:
- 데이터의 하위 집합(또는 루트 노드의 전체 데이터 세트)
- 이 하위 집합의 양성 레이블 비율과 Gini 불순도
- 왼쪽과 오른쪽 자식 노드를 가리키는 포인터(노드가 잎인 경우 None으로 설정)
이 클래스는 새 데이터를 분류하는 데 사용되는 다음 속성도 갖추고 있습니다:
- 입력을 왼쪽이나 오른쪽 자식 노드로 이동시키는 데 사용되는 특징 이름과 임계값(노드가 잎이 아닌 경우)
- (노드가 잎일 경우) 반환할 레이블
이러한 기준을 충족하는 Node 클래스를 아래 코드로 만들 수 있습니다. GitHub의 소스 코드에는 더 철저한 독스트링과 입력 유효성 검사가 포함되어 있지만, 가독성을 위해 여기서 간소화된 버전을 공유하겠습니다. 참고로 이 파일을 node.py로 명명하고 이후 파일에서 참조할 것입니다.
import numpy as np
import pandas as pd
from typing_extensions import Self
class Node:
"""
의사 결정 트리의 노드입니다.
"""
def __init__(
self,
df: pd.DataFrame,
target_col: str
) -> None:
# 훈련용
self.df = df
self.target_col = target_col
self.pk = self._set_pk()
self.gini = self._set_gini()
# 훈련/추론용
self.left = None
self.right = None
# 추론용
self.feature = None
self.threshold = None
def _set_pk(self) -> float:
"""
pk를 설정합니다. 양성 클래스인 샘플의 비율입니다.
샘플은 양성 클래스가 1이고 음성 클래스가 0인 int 배열로 가정합니다.
"""
return np.mean(self.df[self.target_col].values)
def _set_gini(self) -> float:
"""
지니 불순도를 설정합니다.
"""
return 1 - self.pk**2 - (1 - self.pk)**2
현재까지 코드는 가벼운 내용입니다. 데이터프레임(df)과 레이블을 포함하는 열(target_col)을 지정하여 노드를 인스턴스화합니다. 좌측과 우측 자식 노드(self.left, self.right) 및 추론에 사용되는 feature 및 threshold 값을 가진 빈 속성을 생성합니다. 마지막으로, pk(타겟 열에서 1의 비율)와 _set_pk 및 _set_gini 메서드를 사용하여 Gini 불순도를 계산합니다.
이제 기능을 추가하여 특정 feature의 값들을 반복하고 자식 노드에서 최소 지니 불순도를 최소화하는 임계값을 식별하는 논리를 추가해봅시다. split_on_feature 함수는 각 feature의 고유한 값에 대해 _process_split 도우미 함수를 실행합니다. 값 중에 null을 제거한 후 남은 값들이 있으면(잎 노드의 경우 목록이 비어있을 수 있음), 가장 낮은 불순도를 갖는 분할에 대한 Gini 불순도, feature 임계값, 좌우 자식 노드를 반환합니다.
class Node:
...
def split_on_feature(
self,
feature: str
) -> tuple[float, int|float, Self, Self]:
"""
특정 feature의 값을 반복하고 자식 노드에서 가중 Gini 불순도를 최소화하는 분할을 식별합니다.
가중 Gini 불순도, feature 임계값, 좌우 자식 노드의 튜플을 반환합니다.
"""
values = []
for thresh in self.df[feature].unique():
values.append(self._process_split(feature, thresh))
values = [v for v in values if v[1] is not None]
if values:
return min(values, key=lambda x: x[0])
return None, None, None, None
이것이 실제 작업을 수행하는 _process_split입니다. 우리는 self.df를 feature 임계값에 따라 분할하고, 어느 하위 데이터 세트가 비어 있는 경우 일찍 종료하며, 하위 데이터로 자식 노드를 생성하고, 마지막으로 가중 Gini 불순도를 계산합니다.
class Node:
...
def _process_split(
self,
feature: str,
threshold: int|float
) -> tuple[float, int|float, Self|None, Self|None]:
"""
feature 임계값에 따라 데이터 프레임을 분할합니다. 가중 Gini 불순도를 반환하고, 입력된 임계값 및 자식 노드를 반환합니다.
분할 결과가 빈 하위 집합으로 이어지면 Gini 불순도와 None을 반환합니다.
"""
df_lower = self.df[self.df[feature] <= threshold]
df_upper = self.df[self.df[feature] > threshold]
# 임계값이 데이터를 전혀 분할하지 않을 경우 일찍 종료
if len(df_lower) == 0 or len(df_upper) == 0:
return self.gini, None, None, None
node_lower = Node(df_lower, self.target_col)
node_upper = Node(df_upper, self.target_col)
prop_lower = len(df_lower) / len(self.df)
prop_upper = len(df_upper) / len(self.df)
weighted_gini = node_lower.gini * prop_lower \
+ node_upper.gini * prop_upper
return weighted_gini, threshold, node_lower, node_upper
빠르게 테스트해 봅시다. 아래에서 노드를 인스턴스화하고 데이터에 대해 최적의 분할을 찾도록 합니다. split_on_feature는 자식 노드에서 0.0의 가중 Gini 불순도를 반환합니다. 왜냐하면 레이블을 완벽하게 값 2에서 분할할 수 있기 때문입니다. 세 번째 및 네 번째 값은 분할로 생성된 왼쪽 및 오른쪽 자식 노드입니다.
import pandas as pd
df = pd.DataFrame({'feature': [1, 2, 3], 'label': [0, 0, 1]})
node = Node(df, 'label')
print(f"pk: {round(node.pk, 2)}, gini: {round(node.gini, 2)}")
# pk: 0.33, gini: 0.44
print(node.split_on_feature('feature'))
# (0.0, 2,
# <__main__.Node object at 0x137c279d0>,
# <__main__.Node object at 0x137c24160>)
의사 결정 트리
다음 단계는 트레이닝 데이터를 가장 잘 분할하고 새로운 데이터를 가장 정확하게 분류하기 위해 노드를 트리에 배열하는 것입니다. 먼저 기본 구조부터 시작하여 분류기를 학습하고(즉, 트리를 구축하고) 예측을 생성할 수 있는 능력을 살펴봅시다. 우리는 decision_tree.py 파일을 node.py와 동일한 디렉토리에 저장하고 파일에서 Node를 가져옵니다.
우리의 DecisionTree 클래스는 루트 노드로 시작하는데, 이는 df와 target_col로 인스턴스화하는 Node입니다. feature_select은 랜덤 포레스트의 트리를 트레이닝할 때 사용할 feature의 비율을 제어합니다. 기본 의사 결정 트리 클래스에서는 특성의 100%를 기본값으로 사용할 것입니다. max_depth는 트리가 성장할 수 있는 최대 깊이를 지정하는데, 이는 과적합을 방지하는 데 도움이 됩니다.
import numpy as np
import pandas as pd
from .node import Node
class DecisionTree:
"""
의사 결정 트리 분류기, Node로 구성됨
"""
def __init__(
self,
df: pd.DataFrame,
target_col: str,
feature_select: float = 1.0,
max_depth: int = 4
) -> None:
self.root = Node(df, target_col)
self.features = list(df)
self.features.remove(target_col)
self.feature_select = feature_select
self.max_depth = max_depth
이제 트리를 구축하는 논리를 작성해 봅시다. 코딩 면접뿐만 아니라 Leetcode에서 공부한 모든 것이 유용하다는 것을 증명하기 위해 스택을 사용하여 깊이 우선 탐색을 수행하고, 각 노드에서 _process_node를 반복적으로 호출하고 해당 노드의 자식을 스택에 추가합니다. 또한 현재 깊이를 확인하여 self.max_depth를 초과하지 않도록 확인합니다. 모든 노드를 처리한 후에는 DecisionTree 인스턴스를 반환합니다.
class DecisionTree:
...
def build_tree(self) -> None:
"""
깊이 우선 탐색을 사용하여 트리를 구축합니다.
"""
stack = [(self.root, 0)]
while stack:
current_node, depth = stack.pop()
if depth <= self.max_depth:
left, right = self._process_node(current_node)
if left and right:
current_node.left = left
current_node.right = right
stack.append((right, depth+1))
stack.append((left, depth+1))
return self
_process_node에서 실제로 무엇이 발생할까요? 우리는 먼저 특징의 하위 집합을 무작위로 선택한 다음 (또는 self.feature_select가 1.0이면 모든 특징을 선택합니다), 해당 특징을 반복하여 노드의 split_on_feature 메소드를 호출하여 그 특징의 최적 분할을 찾습니다. 그런 다음 자식 노드에서 지니 불순도가 가장 낮아지는 특징을 찾아 현재 노드의 불순도와 비교합니다. 최적의 분할이 더 낮은 불순도를 유발한다면 자식 노드를 반환하고, 그렇지 않으면 순회를 중지해야 함을 나타내기 위해 None을 반환합니다.
class DecisionTree:
...
def _process_node(
self,
node: Node
) -> tuple[Node|None, Node|None]:
"""
특징을 반복하여 자식 노드에서 지니 불순도를 최소화하는 분할을 식별하고
지니 불순도를 가장 많이 줄이는 특징을 식별한 후 해당 특징에 대해
분할된 자식 노드를 반환합니다.
"""
# 무작위로 특징을 선택합니다. self.feature_select = 1.0이면
# 무작위로 선택되지 않습니다 (기본값).
features = list(
np.random.choice(
self.features,
int(self.feature_select*len(self.features)),
replace=False
)
)
# 각 열에 대한 최상의 분할을 위한 지니 불순도 가져오기
d = {}
for col in features:
feature_info = node.split_on_feature(col)
if feature_info[0] is not None
d[col] = feature_info
# 분할할 최적의 열 선택하기
min_gini = np.inf
best_feature = None
for col, tup in d.items():
if tup[0] < min_gini:
min_gini = tup[0]
best_feature = col
# 최상의 분할이 불순도를 줄이는 경우에만 업데이트
if min_gini < node.gini:
# 노드 업데이트
node.feature = best_feature
node.threshold = d[col][1]
return d[col][2:]
return None, None
위의 코드는 트리를 구축하는 데 사용됩니다. 이제 예측을 생성하는 코드를 작성해 봅시다. classify 함수는 _classify 도우미 함수를 감싸는 래퍼일 뿐이며 한 번에 하나씩이 아닌 피처 벡터의 데이터프레임에 대해 예측을 생성할 수 있도록 합니다. 실제 작업은 _classify에서 수행되는데, 이 함수는 피처 벡터가 노드의 임계값과 비교에 따라 왼쪽이나 오른쪽 자식 노드로 재귀적으로 이동합니다. 잎 노드는 피처와 임계값 속성이 모두 None이므로, 노드의 pk가 0.5보다 크면 1을 반환하고 그렇지 않으면 0을 반환합니다.
class DecisionTree:
...
def classify(self, feature_df: pd.DataFrame) -> list[int]:
"""
각 행이 피처 벡터인 데이터프레임이 주어졌을 때, 트리를 탐색하여 예측 레이블을 생성합니다.
"""
return [
self._classify(self.root, f) for i, f in feature_df.iterrows()
]
def _classify(self, node: Node, features: pd.Series) -> int:
"""
피처 벡터가 주어졌을 때, 노드의 자식을 탐색하여 잎에 도달할 때까지 이동한 후, 노드에서 가장 빈번한 클래스를 반환합니다.
긍정적인 레이블과 부정적인 레이블이 동일한 수일 경우, 부정 클래스를 예측합니다.
"""
# 자식 노드
if node.feature is None or node.threshold is None:
return int(node.pk > 0.5)
if features[node.feature] < node.threshold:
return self._classify(node.left, features)
return self._classify(node.right, features)
Random Forest
이제 결정 트리 분류기에 필요한 모든 것을 갖추었습니다! 가장 어려운 작업은 이미 모두 끝났습니다. 분류기를 랜덤 포레스트로 확장하는 것은 이미 _process_node에서 최소화된 피처 선택을 구현했기 때문에 부트스트랩된 데이터에 여러 개의 트리를 생성하는 것만 필요합니다.
랜덤 포레스트를 구현한 random_forest.py 파일을 만들어봅시다. 이 파일에는 RandomForest 클래스가 포함되어 있습니다. 항상처럼, 우리는 클래스를 데이터프레임(df)과 타깃 열로 초기화하고 DecisionTree 클래스와 마찬가지로 feature_select 및 max_depth 매개변수를 가지고 있습니다. 이제 추가로 n_trees 매개변수도 전달합니다.
Markdown 형식으로 테이블 태그를 변경하세요.
import pandas as pd
from .decision_tree import DecisionTree
class RandomForest:
"""
다수의 의사 결정 트리로 구성된 포레스트.
"""
def __init__(
self,
df: pd.DataFrame,
target_col: str,
n_trees: int = 100,
feature_select: float = 0.5,
max_depth: int = 4
) -> None:
self.df = df
self.target_col = target_col
self.n_trees = n_trees
self.feature_select = feature_select
self.max_depth = max_depth
self.forest = []
학습은 간단합니다. 우리는 n_trees 개의 부트스트랩 데이터프레임을 생성하고, 각각에 대해 DecisionTree를 인스턴스화한 다음 각 의사 결정 트리를 훈련시키기 위해 .build_tree를 호출합니다.
class RandomForest:
...
def train(self) -> None:
"""
self.df에 대해 포레스트를 학습합니다.
"""
bootstrap_dfs = [self._bootstrap() for _ in range(self.n_trees)]
self.forest = [
DecisionTree(
bdf,
self.target_col,
self.feature_select,
self.max_depth
)
for bdf in bootstrap_dfs
]
self.forest = [tree.build_tree() for tree in self.forest]
return None
def _bootstrap(self) -> pd.DataFrame:
"""
self.df에서 복원 추출을 통해 행을 샘플링합니다.
"""
return self.df.sample(len(self.df), replace=True)
분류 또한 간단합니다: 우리는 숲 속의 각 트리가 입력된 feature_df를 분류하고, 각 행에 대해 가장 일반적인 예측 레이블을 반환하도록 합니다. 이 작업을 하는 가장 쉬운 방법은 예측을 데이터프레임으로 변환한 다음, 최빈값을 취하는 것이었습니다.
class RandomForest
...
def classify(self, feature_df: pd.DataFrame) -> int:
"""
입력된 feature 벡터를 분류합니다. 숲 속의 각 트리는 예측 레이블을 생성하고,
각 feature 벡터에 대해 가장 일반적인 레이블이 반환됩니다.
"""
preds = pd.DataFrame(
[tree.classify(feature_df) for tree in self.forest]
)
# 가장 일반적인 예측 레이블 반환
return list(preds.mode().iloc[0])
그리고... 이게 전부입니다! run.py 스크립트를 실행하면 DecisionTree 분류기, RandomForest의 평균 트리, 전체 RandomForest, 그리고 scikit-learn의 RandomForestClassifier의 정확도를 비교할 수 있습니다. 결과는 데이터셋, 숲당 트리 수 등에 따라 다를 수 있지만, 우리가 한 결정 트리가 숲의 평균 트리보다 더 높은 정확도를 가지고 있고, 전체 랜덤 포레스트가 개별 트리보다 훨씬 강하다는 것을 볼 수 있습니다. 역시 scikit-learn이 가장 높은 정확도를 보여주죠... 하지만 우리도 나쁘지 않았습니다!
정확도
* 단일 의사결정 트리: 0.61
* 평균 랜덤 포레스트 트리: 0.595
* 전체 랜덤 포레스트: 0.81
* scikit-learn 랜덤 포레스트: 0.89

결론
이 게시물에서는 랜덤 포레스트(Random Forest)라는 가장 인기 있고 강력한 머신 러닝 알고리즘 중 하나를 다루었습니다. 이론부터 시작하여 결정 트리가 데이터 세트를 분할하는 데 가장 적합한 기능 값을 식별하기 위해 Gini 불순도와 같은 지표를 사용하는 방법을 설명했습니다. 그리고 Gini 불순도를 가장 많이 감소시키는 최적 분할 기능을 반복적으로 식별하여 트리를 구축하는 방법을 보여주었습니다. 또한 무작위 특성 선택 및 부트스트랩 데이터 세트를 사용하여 수십 개의 결정 트리로 구성된 랜덤 포레스트를 구축하는 방법을 설명했습니다. 마지막으로 몇 가지 코드를 작성하여 해당 이론을 테스트했습니다.
더 알고 싶다면 미니 프로젝트가 많이 있습니다. 동일한 기능이 대상 변수와 매우 비선형적인 관계를 가질 경우 트리에서 여러 번 사용될 수 있는 방법을 시각화해 볼 수 있습니다. 이 게시물에서 회귀에 대해 다루지 않았지만, 연속적인 대상을 처리할 수 있도록 코드를 수정하는 것은 그리 어렵지 않을 것입니다. 데이터 양과 열의 수에 따른 일반 DecisionTree, 평균 랜덤 포레스트 트리 및 전체 포레스트의 예측력이 어떻게 달라지는지 확인하는 것도 흥미로울 것입니다. 마지막으로, RandomForest가 어떻게 트리를 학습하는지를 병렬화하고 싶은 사람이 있다면 PR을 제출해 주시기 바랍니다. 😜
친절하게 읽어 주셔서 감사합니다! Matt
1. 의사 결정 트리 훈련
이 그림은 정말 마음을 쏙 들인 작품이었습니다. 곡선과 원들이 한 색에서 다른 색으로 전환되는 방법을 알아내는 것이 어려웠는데, 놀랍게도 가장 어려웠던 부분은 x와 체크 마크를 원 안에 깔끔하게 유지하면서 너무 많이 뭉쳐지지 않게 하는 것이었습니다. 이 그림의 아이콘과 색상을 너무 많이 바꿔서 결국 스크립트를 작성해서 생성하는 것으로 끝이 났죠.
여기에는 장난감 예제(분할 모양)와 포스트의 주요 예제(전자 상거래)와 더 명확한 시각적 구분이 필요하다고 생각하기 전까지 일부 버전의 그림이 있습니다.
2. 랜덤 포레스트
아래 코드를 사용하여 동일한 데이터 세트에 대해 sklearn이 동일한 결정 트리를 출력하는지 직접 확인할 수 있습니다. 랜덤 상태를 동일하게 지정해야한다는 점을 주의하세요.
import numpy as np
import pandas as pd
from sklearn.tree import DecisionTreeClassifier
# 매개변수
random_state = 42
# 데이터 생성
df = pd.DataFrame(
{
'feature_1': np.random.normal(0, 1, 100),
'feature_2': np.random.normal(1, 1, 100),
'label': np.random.choice([0, 1], 100)
}
)
mod1 = DecisionTreeClassifier(random_state=random_state)
mod1.fit(df[['feature_1', 'feature_2']], df['label'])
mod2 = DecisionTreeClassifier(random_state=42)
mod2.fit(df[['feature_1', 'feature_2']], df['label'])
comparison = (mod1.tree_.value == mod2.tree_.value)
print(comparison.all())
# True