• 이 게시물에서는 기술적, 근본적 분석 도구 및 현대 포트폴리오 최적화(PO) 알고리즘을 통합하여 파이썬에서 미국 대형 기술 기업들의 양적 거래 분석에 초점을 맞추고 있습니다.

미국의 대형 기술 기업이란?

• 빅 포 (알파벳, 아마존, 애플, 메타)
• 빅 파이브 (알파벳, 아마존, 애플, 메타, 마이크로소프트)
• 멋진 일곱 (알파벳, 아마존, 애플, 메타, 마이크로소프트, 엔비디아, 테슬라)
• 기타: 보고서에 따르면 AMD는 2023년 이후 브랜드 성장을 상당히 경험했으며, 전년대비 53% 증가했습니다. 또한 AMD의 브랜드 가치가 비즈니스 기술 및 서비스 플랫폼 부문에서 5186만 달러에 달했습니다. 그 강한 성장이 어디서 비롯된 것인지 쉽게 추측할 수 있습니다. AMD는 최근 몇 년 동안 경쟁사 인텔과 엔비디아가 해 온 것처럼 AI에 주력하고 있습니다.

비즈니스 케이스

• 최근 몇 년간 미국 주식 시장은 빅테크가 주도한 놀라운 성장 기회를 제공해 왔습니다. 하지만, 상승장이 계속될 수 있을까요?
• 빅테크 기업들은 역사상 가장 큰 반독점 입법 파동에 직면하고 있습니다.
• 세계적인 세금 전쟁이 임박했습니다. 이는 빅테크에 큰 타격을 줄 수 있습니다.
• 결론: 이러한 인상적인 성과에도 불구하고, 현재의 고 인플레이션과 이자율 경제환경에서 특히 높은 가치평가를 받는 기술 주식에 베팅하는 것에 대해 투자자들은 조심해야 합니다. Nvidia 칩과 Meta의 대형 언어 모델과 같은 AI 응용 프로그램은 약속을 보이지만, 이들의 시장가치는 실제 소비자 혜택과 실현된 생산성 향상에 궁극적으로 의존할 것입니다.

프로젝트 목표

• 우리의 궁극적인 목표는 기술적 분석 (TA) 지표, 주식 기초 내용 및 위험과 수익을 동시에 고려하는 포트폴리오 최적화를 통합하는 것입니다.
• Markowitz (1952) [1]는 투자 포트폴리오의 다양성을 옹호하며, 이 과정이 투자의 분산을 줄인다는 것을 입증했습니다.
• 이 다양성 개념들은 Modern Portfolio Theory (MPT)을 불러일으켰는데, 이는 위험과 수익이라는 두 가지 상충하는 목표 사이에서 선택하는 아이디어를 가져왔습니다.
• TA 지표는 자산 가격과 거래량의 추세를 식별하기 위해 시장 참가자들에 의해 널리 사용됩니다. 최근 연구에 따르면 [2], 우리는 MPT와 TA 간의 격차를 줄이기 위해 TA 신호의 최적 가중치를 직접 다중 TA 신호의 함수로 매개변수화된 PO 전략을 개발했습니다.
• 일부 거래자들은 FA 대신 TA를 선호하지만, 가장 성공적인 전략은 종종 두 가지를 조화롭게 적용한 것에서 나옵니다. 이는 거래자들이 즉각적인 가격 변동과 장기적인 경제 예측에서 모두 이익을 취할 수 있도록 하며 [3], 이 통합된 PO 접근 방식은 시장 역학을 이해하는 것을 강화할 뿐만 아니라 거래자들이 견고한 투자 결정을 내리기 위한 포괄적인 도구 상자를 제공합니다.

기술 분석 (TA)

• TA는 시장을 분석하는 프레임워크를 트레이더에 제공하여 트렌드, 지지/저항 수준 및 진입/퇴출 지점을 식별하는 데 도움을 줍니다 [5].
• TA의 두 가지 주요 가정은 다음과 같습니다 [5]: (1) 보안 가격은 기본적인 요소를 포함한 모든 중요한 정보를 반영한다; (2) 가격 변동은 상승, 하락 또는 측면 추세를 따른다.

근본 분석 (FA)

• TA는 단기적인 패턴만 식별하는 반면, FA는 주식 가격이 실제 가치를 저평가(또는 고평가)하는 자산을 강조할 것입니다 [5, 7].
• 간단히 말해, 스마트한 투자 결정을 내리는 것이 FA의 주요 이점입니다. 이는 회사가 얼마나 벌고 지출하는지, 얼마나 많은 제품을 판매하는지 및 외부 요소에 어떻게 영향을 받는지를 이해하는 것을 포함합니다 [7].

TA vs FA

• FA(기업 재무 분석)는 자산의 품질에 초점을 맞추고, TA(기술적 분석)는 시장 동향을 가치의 지표로 삼습니다. 두 방법 모두 주식 가격의 미래 동향을 예측하는 데 사용됩니다.

포트폴리오 최적화

• PO(포트폴리오 최적화)는 투자자가 자산을 선택하여 재무 위험을 최소화하고 ROI를 극대화하는 프로세스입니다.
• 투자 수익률(ROI)은 모든 산업에서 익숙한 지표입니다.
• 재정적으로 위험은 투자 수익이 기대와 다를 가능성을 의미합니다.

도구들:

• Quantstats는 포트폴리오 분석을 위한 광범위한 기능을 제공합니다. 양적 분석가, 트레이더 및 포트폴리오 매니저를 대상으로 하며, 투자 전략에 대한 보다 깊은 통찰력을 얻고자 하는 사용자를 위해 설계되었습니다.
• TA는 금융 시계열 데이터 세트에 대한 TA 라이브러리입니다. 금융 시계열 데이터 세트(오픈, 클로즈, 하이, 로우, 볼륨)에서 피쳐 엔지니어링을 수행하는 데 유용합니다. Pandas와 Numpy에 기반을 두고 있습니다.
• PyPortfolioOpt는 전통적인 MPT 및 Black-Litterman 할당뿐만 아니라 Shrinkage, Hierarchical Risk Parity와 같은 분야의 최근 개발사항들을 구현하는 라이브러리입니다. 또한, 지수 가중 공분산 행렬과 같은 혁신적인 실험적 기능도 포함하고 있습니다.
• FinanceToolkit은 가장 단순한 방식으로 150가지 이상의 재무 비율, 지표 및 성과 측정 항목이 포함된 오픈 소스 툴킷입니다. 이 툴킷은 주식에만 국한되지 않고, 옵션, 화폐, 암호화폐, ETF, 상장펀드, 지수, 머니 마켓, 상품, 주요 경제 지표 등에 대한 역사적 데이터 및 샤프 비율, VaR과 같은 중요한 성과 및 위험 측정 수단을 얻기 위해 사용할 수 있습니다.

자료

• 금융 시장을 위한 데이터 과학
• FinanceToolkit 예제
• 주식 시장 트렌드 및 Value at Risk

프로젝트 마일스톤

• 빅 포 매칭 2020-2024 (BF)의 기초적인 리스크-수익 분석
• 등가치 가중 BF 포트폴리오의 성과 분석
• Sharpe Ratio 최대화를 위한 BF 최적화 (효율적 투자선) vs S&P 500
• (NVDA, AMD) vs 벤치마크 누적 수익률 및 VaR
• (NVDA, AMD) 수익성 분석 및 그리스 감도
• NVDA 및 AMD의 Fama-French 요인과의 상관 관계
• (AAPL, AMZN, META, MSFT, GOOG) 재무 분석 및 주가 시뮬레이션
• TA 이치모쿠 클라우드 차트: NVDA vs AMD
• META 주식 TA, RSI vs EMA 전략 백테스팅

위의 프로젝트 마일스톤에 대해 깊이 있게 탐구하는 포괄적인 안내서입니다. 해당 프로젝트는 가상 안콘다 환경을 생성한 후 주피터 노트북에서 구현되었습니다.

기본 임포트 및 설치

• 필요한 Python 라이브러리 설치 및 불러오기

!pip install quantstats, ta, pypfopt, plotly, yfinance, sklearn, seaborn, scipy

# 라이브러리 불러오기

# 데이터 처리 및 통계 분석 
import pandas as pd
#from pandas_datareader import data
import numpy as np
from scipy import stats

# 데이터 시각화 
import matplotlib.pyplot as plt
import seaborn as sns
import plotly.express as px
import plotly.graph_objects as go
from plotly.subplots import make_subplots

# 최적화 및 자산 할당
from pypfopt.efficient_frontier import EfficientFrontier
from pypfopt import risk_models
from pypfopt import expected_returns
from pypfopt import black_litterman, BlackLittermanModel

# 금융 데이터 
import quantstats as qs
import ta
import yfinance as yf

# 선형 회귀 모델
from sklearn.linear_model import LinearRegression

# Plotly 오프라인 모드 활성화
from plotly.offline import init_notebook_mode
init_notebook_mode(connected=True)


# 포트폴리오 최적화를 위한 라이브러리 불러오기
from pypfopt.efficient_frontier import EfficientFrontier
from pypfopt import risk_models
from pypfopt import expected_returns

# 날짜 및 경고 숨기기 
import datetime as dt
import warnings
warnings.filterwarnings("ignore")

2020–2024 빅 포 팝 4 (BF) 기본 수익-변동성 분석

• 입력된 BF 주식 데이터 2020-2024년을 읽는 중

#Big Four
tickers = ["AAPL", "GOOG","AMZN","META"] 
aapl = qs.utils.download_returns(tickers)
aapl = aapl.loc['2020-01-01':'2024-07-10']

• BF 주식의 일일 수익률 그래픽 표시

# 각 주식의 일일 수익률 그래픽 표시
print('\n')
print('\n주식 일일 수익률 그래픽:\n')
qs.plots.daily_returns(aapl,benchmark='SPY')

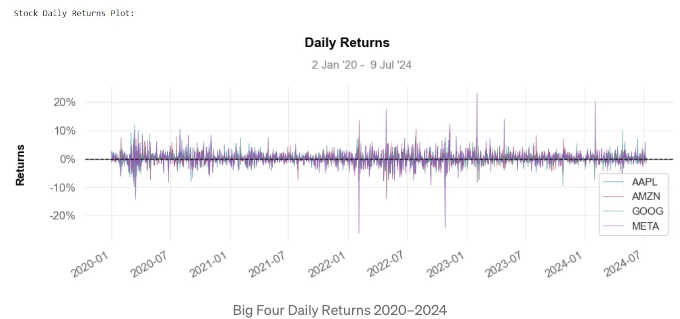
• 주식의 성과를 평가하는 가장 좋은 방법 중 하나는 일일 수익률을 계산하는 것입니다.
• 위에 있는 플롯은 기본적으로 주식 가치가 하루 동안 얼마나 변화했는지 보여줍니다. 이 기본 정보를 사용하여 회사에 더 많이 투자하거나 다른 곳에 투자를 시도할지 결정할 수 있습니다.
• BF 주식 누적 수익 그래플 작성

# 각 주식에 대한 누적 수익 그래프 작성
print('\n')
print('\nStock Cumulative Returns Plot\n')
qs.plots.returns(aapl)

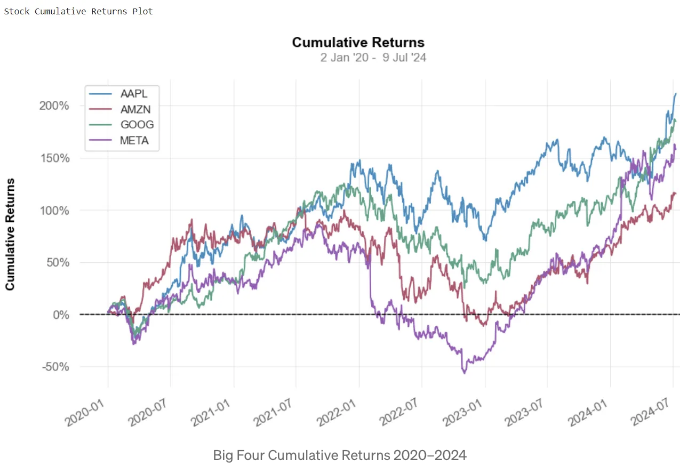
• 누적 수익 대비는 일정 기간 동안 투자 가격의 총 변화를 의미합니다.
• 이것은 물가 상승 및 기타 외부 요인의 영향을 고려하지 않는 총 명목 수익입니다.
• 양의 수익은 이익을 나타내고, 음의 수익은 손실을 나타냅니다.
• 세금은 대부분의 투자에 대한 누적 수익을 상당히 줄일 수 있습니다.

BF의 첨도

• BF 일일 수익의 첨도를 계산하고 그래프로 나타내기

# 첨도를 측정하기 위해 quantstats 사용
print('\n')
print("BF의 첨도: ", qs.stats.kurtosis(aapl).round(2))

AAPL     5.03
AMZN     4.00
GOOG     3.63
META    17.71
dtype: float64

qs.stats.kurtosis(aapl).round(2).plot.bar(label='첨도')
plt.legend()

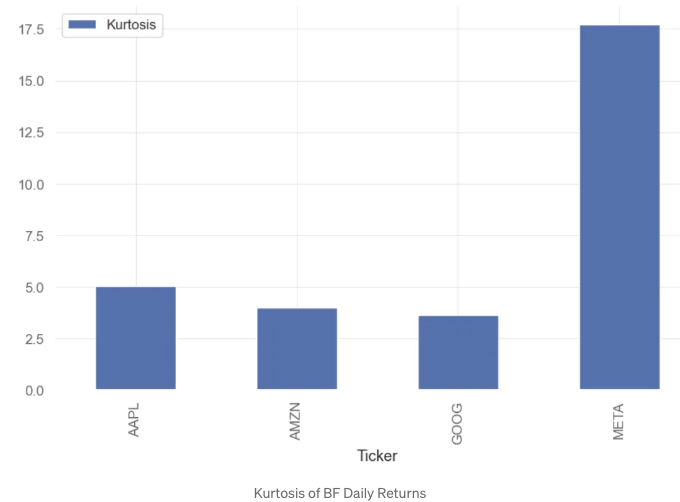
• 첨도(Kurtosis)는 분포의 꼬리 모양을 측정합니다.
• 금융 분석에서 첨도는 투자의 가격 변동성 리스크를 측정하는 데 사용됩니다. 첨도는 투자의 가격이 정기적으로 경험하는 변동성을 측정합니다. 수익 분포의 높은 첨도는 투자가 가끔 극단적인 수익을 내줄 것을 시사합니다. 높은 첨도는 큰 양의 양수 수익 또는 극단적인 음수 수익을 나타낼 수 있다는 것을 염두에 두세요.
• 우리는 BF의 일일 수익을 첨두관련 분포(첨도 ` 3.0)로 간주할 수 있습니다. 이 분포는 긴 꼬리(이상치)를 가진 곡선으로 나타납니다.
• 추론: kur(META) `` kur(AAPL) ` kur(AMZN) ~ kur(GOOG)

BF의 왜도(Skewness)

• BF의 일일 수익의 왜도(Skewness)를 계산하고 그래프에 표시하기

# Quantstats를 사용하여 왜도 측정
print('\n')
print("주식 왜도: ", qs.stats.skew(aapl).round(2))

주식 왜도:  Ticker
AAPL    0.12
AMZN    0.12
GOOG   -0.06
META   -0.29
dtype: float64

qs.stats.skew(aapl).round(2).plot.bar(label='Skewness')
plt.legend()

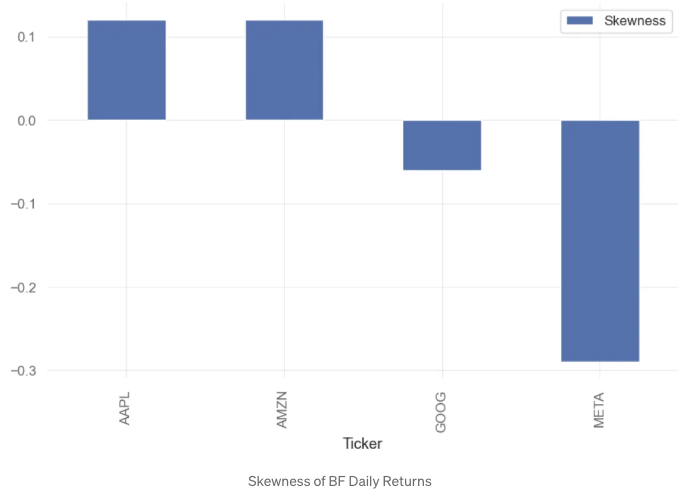
• 왜도는 데이터가 대칭적 벨 곡선에서 벗어나는 방향과 정도를 나타냅니다.
• 왜도가 0인 분포는 완전히 대칭적이며 분포의 왼쪽과 오른쪽이 거울 이미지인 것을 의미합니다. 양수 왜도는 오른쪽 꼬리가 왼쪽보다 길거나 더 두껍다는 것을 의미하며, 데이터가 높은 값을 가질 가능성이 높음을 시사합니다. 음수 왜도는 왼쪽 꼬리가 오른쪽보다 길거나 더 두꺼워 낮은 값을 가질 가능성을 시사합니다.
• 일반적으로 -0.5 ~ 0.5 사이의 값은 약간의 왜도 수준을 나타냅니다.
• 추론: skew(META)=-0.29
• 실현 왜도와 미래 가격 간에 부정적인 교차 섹션이 관찰됩니다. — 음수 왜도를 가진 주식은 높은 변동성에 대해 미래 수익이 높게 보상됩니다.
• GOOG의 부정적인 왜도는 투자자가 빈번한 소규모 이익과 소수의 큰 손실을 기대할 수 있다는 것을 의미합니다. 실제로, 많은 거래 전략이 부정적으로 왜도된 분포에 기초합니다.
• AAPL 및 AMZN의 0에서 적정한 양수의 왜도와 결합되면, 이러한 분포는 안정적인 수익과 낮은 리스크를 시사할 것입니다.

BF의 표준 편차

• BF 일별 수익률의 표준 편차(STD)를 계산하고 그래프로 플로팅합니다.

# 표준 편차 계산하기
print('\n')
print("주식 표준 편차: ", aapl.std().round(3))

주식 표준 편차:  Ticker
AAPL    0.021
AMZN    0.023
GOOG    0.021
META    0.029
dtype: float64

aapl.std().round(3).plot.bar(label='STD')
plt.legend()

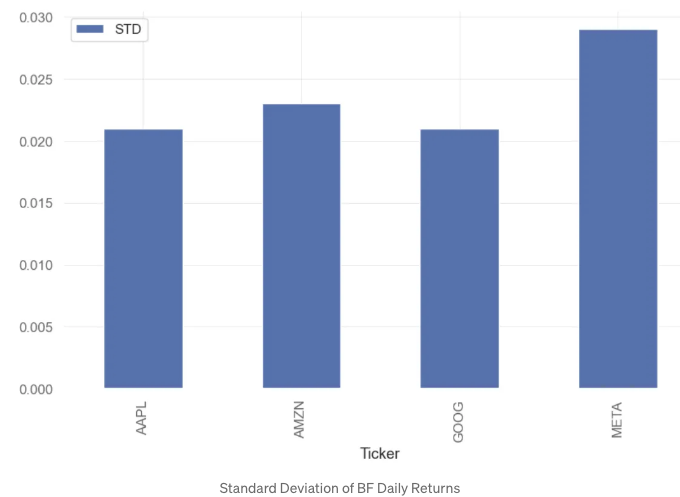
• 표준 편차는 투자를 비교하는 기본적인 방법으로, 데이터의 변동이나 분산을 측정합니다. 더 높은 표준 편차는 더 높은 위험을 의미합니다.
• 데이터 포인트가 평균에서 더 멀리 떨어져 있는 경우 데이터 세트 내에서 더 높은 편차가 있습니다. 표준 편차는 분산의 제곱근으로 계산됩니다.
• 변동성이 큰 주식은 표준 편차가 높고, 안정적인 블루 칩 주가 주식의 편차는 보통 낮습니다.
• 결론: std(AAPL, AMZN, GOOG) 약 0.02, std(META) 약 0.03입니다.

BF 상관 분석

• 페어 플롯(pairplot)과 상관 행렬은 자산 간의 상관 관계를 시각화하는 데 유용한 도구입니다.
• BF 일일 수익의 페어 플롯을 생성합니다.

# 페어 플롯
sns.pairplot(aapl, kind='reg')
plt.show()

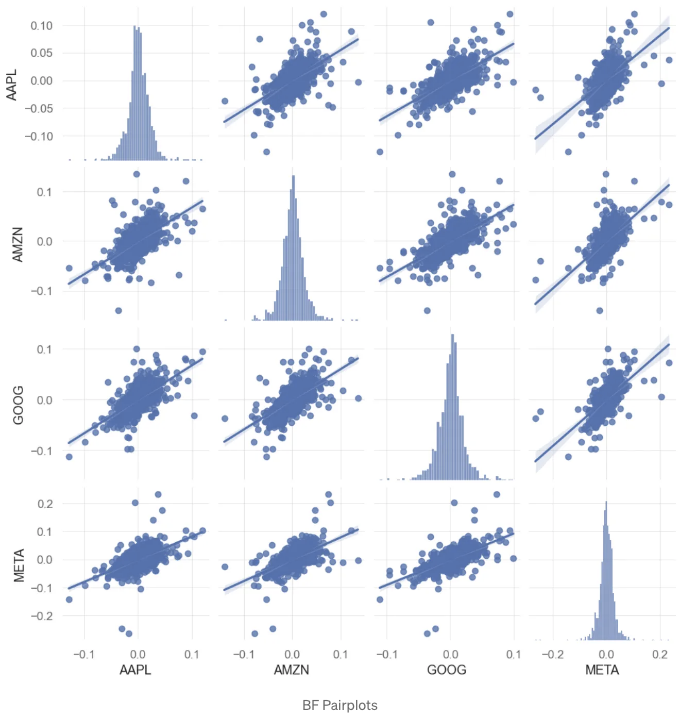
• 위의 플롯은 구글과 메타 주식 간의 흥미로운 선형 관계를 보여줍니다.
• BF 일일 수익의 상관 행렬을 플로팅한 결과입니다.

# 상관 행렬
corr = aapl.corr()
mask = np.zeros_like(corr, dtype=bool)
mask[np.triu_indices_from(mask)] = True
sns.heatmap(corr, annot=True, mask=mask)
plt.show()

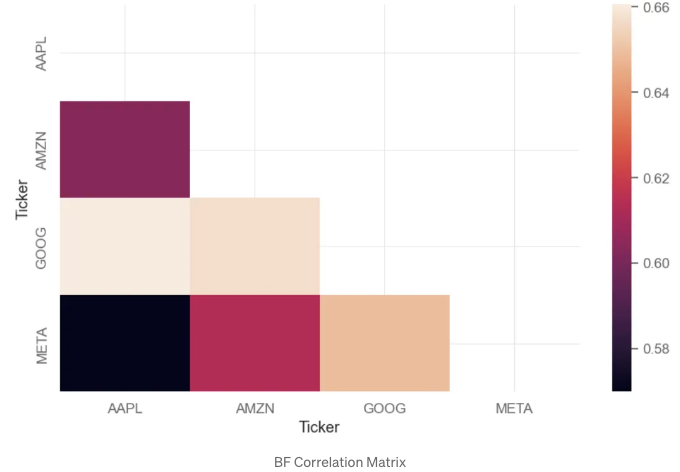
• GOOG와 AAPL, AMZN, META의 3개 주식 간에는 0.64~0.66 정도의 강한 양의 상관 관계가 있습니다.

BF의 베타 계수

• 주식의 베타 계수는 시장 기준으로 시간이 지남에 따른 변동성을 측정하는 지표입니다. 1의 베타는 주식의 변동성이 시장과 정확히 일치한다는 것을 의미합니다. 더 높은 베타는 큰 변동성을 나타내고, 낮은 베타는 덜한 변동성을 나타냅니다.
• BF의 벤치마크 SPY에 대한 베타 계수를 계산하기 위해 선형 회귀 분석을 사용합니다.

bench = ["SPY"] 
spy = qs.utils.download_returns(bench)
spy = spy.loc['2020-01-01':'2024-07-10']

# 인덱스 제거
spy_no_index = spy.reset_index(drop = True)
aapl_no_index = aapl.reset_index(drop = True)

# 애플의 수익률과 벤치마크 사이의 선형 관계 설정

자산='AAPL'
X = spy_no_index.values.reshape(-1,1)
y = aapl_no_index[asset].values.reshape(-1,1)

linreg = LinearRegression().fit(X, y)

베타 = linreg.coef_[0]
알파 = linreg.intercept_
print('\n')
print('AAPL 베타: ', beta.round(3))
print('\nAAPL 알파: ', alpha.round(3))


자산_베타 = []
자산_베타.append(베타.round(3)[0])

AAPL 베타:  [1.203]

AAPL 알파:  [0.001]

자산='AMZN'
X = spy_no_index.values.reshape(-1,1)
y = aapl_no_index[asset].values.reshape(-1,1)

linreg = LinearRegression().fit(X, y)

베타 = linreg.coef_[0]
알파 = linreg.intercept_
print('\n')
print('AMZN 베타: ', beta.round(3))
print('\nAMZN 알파: ', alpha.round(3))

자산_베타.append(베타.round(3)[0])

AMZN 베타:  [1.075]

AMZN 알파:  [0.]

자산='META'
X = spy_no_index.values.reshape(-1,1)
y = aapl_no_index[asset].values.reshape(-1,1)

linreg = LinearRegression().fit(X, y)

베타 = linreg.coef_[0]
알파 = linreg.intercept_
print('\n')
print('META 베타: ', beta.round(3))
print('\nMETA 알파: ', alpha.round(3))

자산_베타.append(베타.round(3)[0])

META 베타:  [1.324]

META 알파:  [0.001]

자산='GOOG'
X = spy_no_index.values.reshape(-1,1)
y = aapl_no_index[asset].values.reshape(-1,1)

linreg = LinearRegression().fit(X, y)

베타 = linreg.coef_[0]
알파 = linreg.intercept_
print('\n')
print('GOOG 베타: ', beta.round(3))
print('\nGOOG 알파: ', alpha.round(3))

자산_베타.append(베타.round(3)[0])

GOOG 베타:  [1.139]

GOOG 알파:  [0.]

print(자산_베타)
[1.203, 1.075, 1.324, 1.139]

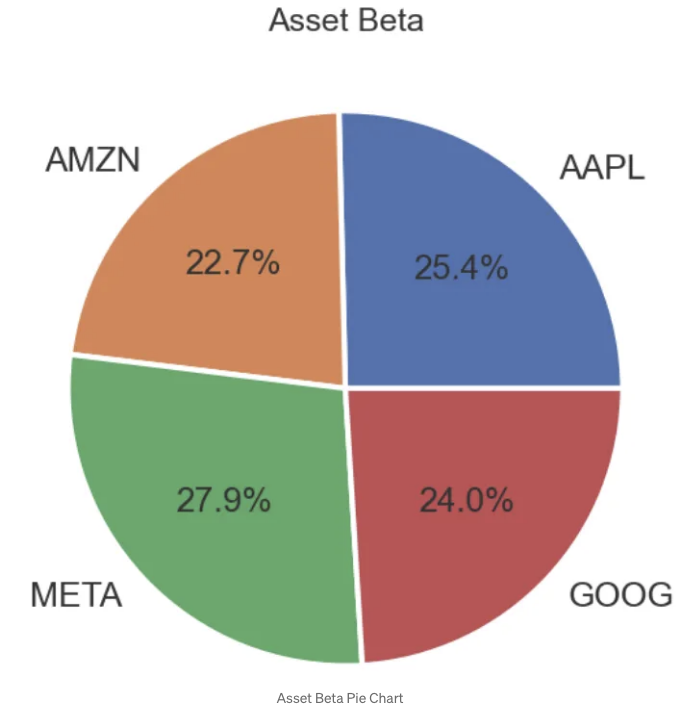
• BF의 베타 계수를 플로팅하기

fig, ax = plt.subplots(figsize=(6, 6))

x = asset_beta
tickers1=['AAPL', 'AMZN', 'META', 'GOOG']

ax.pie(x, labels=tickers1, autopct='%.1f%%',
       wedgeprops={'linewidth': 3.0, 'edgecolor': 'white'},
       textprops={'size': 'x-large'})
ax.set_title('Asset Beta', fontsize=18)
plt.tight_layout()

#import numpy as np
#import matplotlib.pyplot as plt
 
courses = tickers
values = x
 
fig = plt.figure(figsize=(10, 5))

# creating the bar plot
plt.bar(courses, values, color='maroon', width=0.4)

plt.xlabel("Assets")
plt.ylabel("Beta Value")
plt.title("Asset Beta Values")
plt.show()

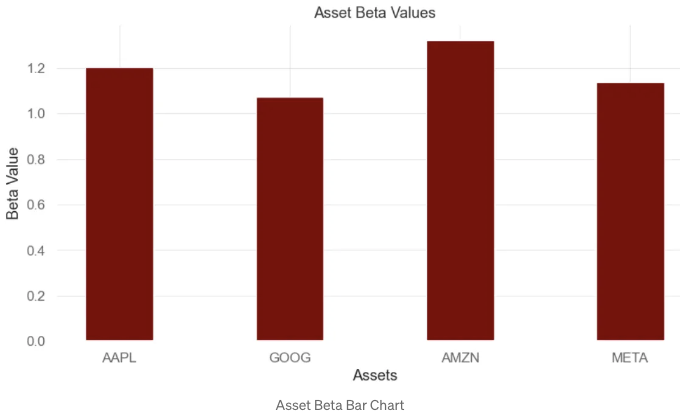
• 정의상 S&P 500 지수와 같은 시장은 베타가 1.0이며, 개별 주식은 시장과 얼마나 벗어나는지에 따라 순위가 매겨집니다.
• 추론: BF 주식은 베타가 1.0보다 높기 때문에 시간이 지남에 따라 시장보다 더 많이 흔듭니다.

BF의 샤프 비율

• 샤프 비율은 투자의 위험 조정 수익률을 측정하는 지표입니다.
• BF의 샤프 비율을 계산하고 시각화합니다.

# 샤프 비율 계산
print('\n')
print("주식의 샤프 비율: ", qs.stats.sharpe(aapl).round(2))
주식의 샤프 비율: Ticker
AAPL 0.93
AMZN 0.65
GOOG 0.87
META 0.69
dtype: float64

qs.stats.sharpe(aapl).round(2).plot.bar(label='샤프 비율')
plt.legend()

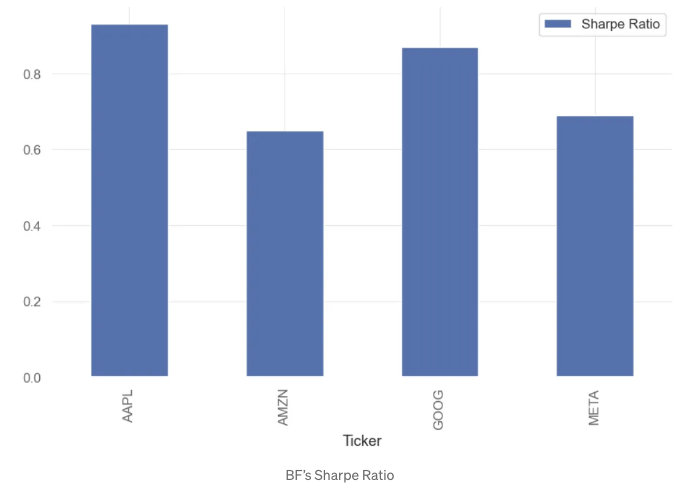
• Sharpe ratio가 높을수록 투자가 다른 Sharpe ratio가 낮은 투자에 비해 주어진 위험 수준에서 더 높은 수익을 제공함을 나타냅니다.
• 결론: AAPL은 다른 3개 주식 (AMZN, GOOG, META)에 비해 주어진 위험 수준에서 더 높은 수익을 제공할 수 있습니다. AAPL의 Sharpe ratio가 거의 1에 가깝다는 것은 투자의 평균 수익이 리스크-프리 이자율과 거의 같다는 것을 의미합니다.

등중 BF 포트폴리오의 성과 분석

• 등중 BF 포트폴리오의 성과를 살펴봅시다.
• 각 보안의 가중치 = 포트폴리오 내 보안 수로 1을 나눈 값
• 4개 주식으로 이루어진 BF 포트폴리오에서 각 주식은 25%의 가중치를 가집니다.

weights = [0.25, 0.25, 0.25, 0.25] # 각 주식의 가중치 정의
ap=aapl['AAPL']
am=aapl['AMZN']
me=aapl['META']
ms=aapl['GOOG']
portfolio = ap*weights[0] + am*weights[1] + me*weights[2] + ms*weights[3] # 각 주식을 해당 가중치로 곱하여 포트폴리오 생성
portfolio # 포트폴리오의 일일 수익률 표시

Date
2020-01-02    0.023684
2020-01-03   -0.008015
2020-01-06    0.016586
2020-01-07   -0.000268
2020-01-08    0.006574
                ...   
2024-07-02    0.012870
2024-07-03   -0.000289
2024-07-05    0.029234
2024-07-08   -0.006084
2024-07-09    0.001275
Length: 1136, dtype: float64

• 포트폴리오의 일일 수익률, 히스토그램, 누적 수익률 플로팅

portfolio.plot()

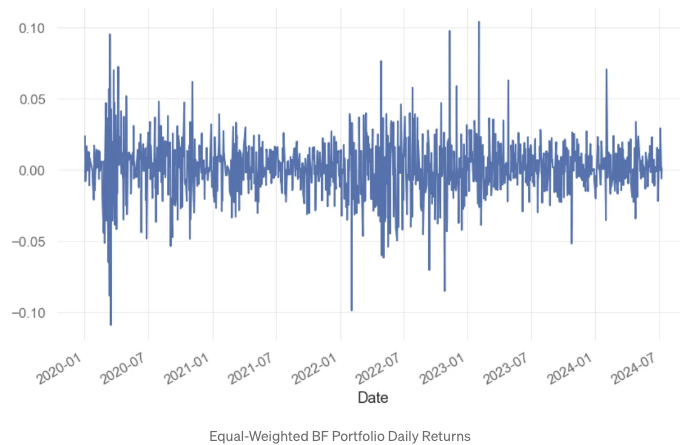
portfolio.hist()

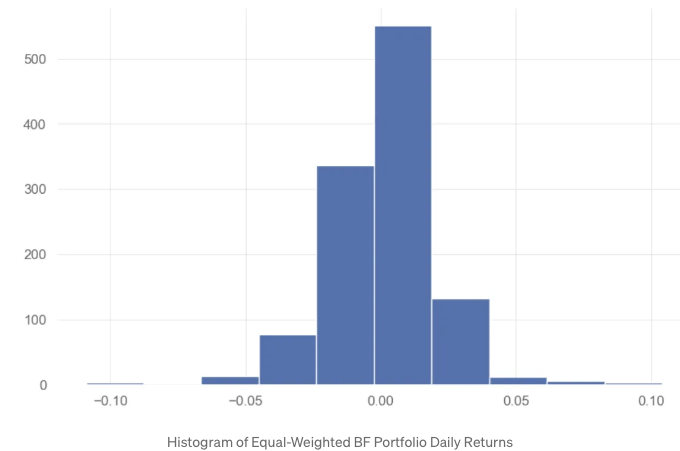
qs.plots.returns(portfolio)

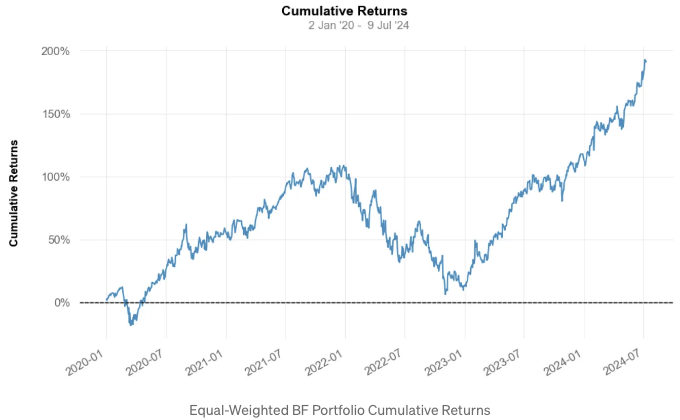
• Equal-Weighted BF 포트폴리오 성과 보고서 및 전략 시각화 vs SPY 기준 생성 중입니다!

qs.reports.full(portfolio, benchmark = spy)

성과 지표
                           기준          전략
-------------------------  -----------  ----------
시작 기간                 2020-01-02   2020-01-02
종료 기간                 2024-07-09   2024-07-09
무위험 이자율             0.0%         0.0%
시장 참여 시간            100.0%       100.0%

누적 수익률               72.69%       191.47%
CAGR﹪                    8.7%         17.75%

샤프 지수                 0.67         0.91
확률적 샤프 비율          91.92%       97.3%
스마트 샤프                0.6          0.82
소르티노 지수              0.93         1.31
스마트 소르티노             0.84         1.18
소르티노/√2                0.66         0.93
스마트 소르티노/√2         0.59         0.83
오메가                     1.18         1.18

최대 하락폭               -34.1%       -49.12%
최장기 하락일             745          690
변동성 (연간)             21.66%       31.42%
R^2                      0.67         0.67
정보 비율                 0.05         0.05
칼마르 비율               0.26         0.36
비대칭도                   -0.54        -0.14
첨도                     11.14        4.01

예상 일일 %              0.05%        0.09%
예상 월별 %              1.0%         1.96%
예상 연간 %              11.55%       23.86%
켈리 기준                4.81%        5.39%
파산 위험                 0.0%         0.0%
일일 VaR                 -2.19%       -3.14%
예상 손실 (cVaR)         -2.19%       -3.14%

최대 연속 승리           10           8
최대 연속 패배           7            6
이익/통곽 비율          0.14         0.18
이익/통곽 (1M)          0.7          1.12

상환 비율                0.92         0.96
이익 요소               1.14         1.18
상식적 비율              1.08         1.14
CPC 지수                0.57         0.61
테일 비율               0.95         0.97
이상치 승률             4.9          3.06
이상치 손실률           4.78         3.19

MTD                     2.13%        5.18%
3M                      7.15%        16.73%
6M                      17.11%       36.32%
YTD                     16.94%       34.8%
1Y                      26.74%       54.69%
3Y (연간)              5.54%        9.97%
5Y (연간)              8.7%         17.75%
10Y (연간)             8.7%         17.75%
전체 기간 (연간)       8.7%         17.75%

최고 효과 일             9.06%        10.41%
최악의 날               -10.94%      -10.9%
최고 월                  12.7%        20.41%
최악의 월               -13.0%       -15.13%
최고 연도               27.04%       91.38%
최악의 연도             -19.48%      -44.71%

평균 하락                  -2.12%       -3.55%
평균 하락 일             21           23
회복 계수                1.91         2.63
울서 지수                0.1          0.18
평정 지수                0.44         0.42

월별 상승 평균           4.73%        7.66%
월별 하락 평균           -5.82%       -7.11%
이익 일 %                 54.41%       53.7%
이익 월 %                63.64%       65.45%
이익 분기 %              73.68%       68.42%
이익 연도 %              80.0%        80.0%

베타                       -            1.19
알파                      -            0.12
상관관계               -            81.71%
Treynor Ratio           -            161.56%
없음


최악 5 번 하락

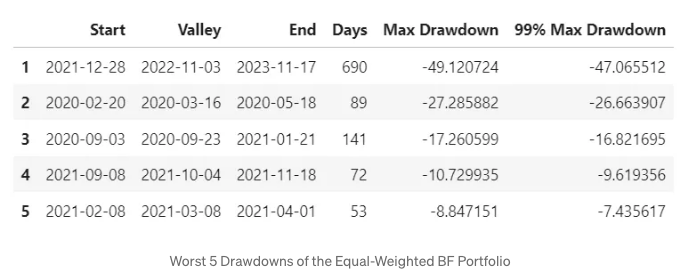
• 전략 시각화 대 SPY 벤치마크

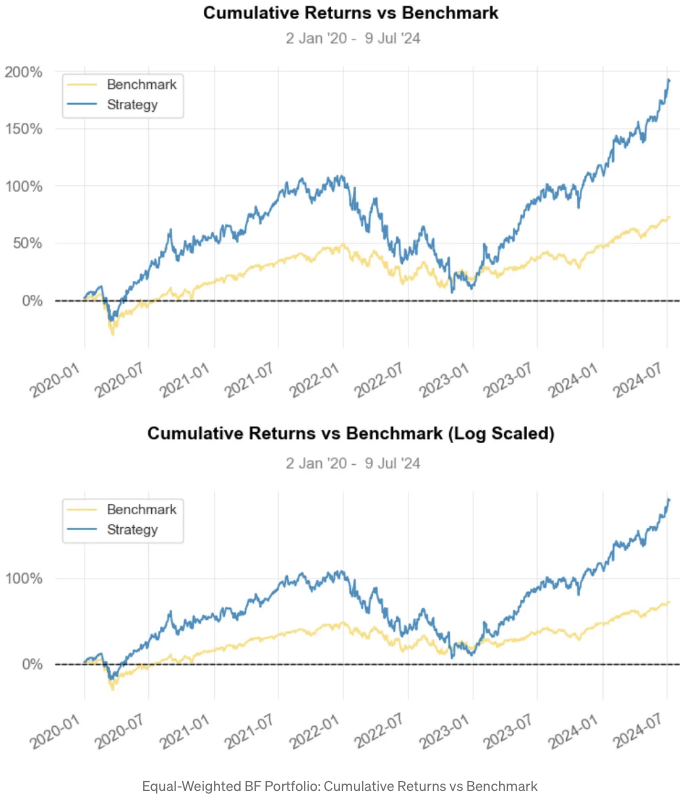
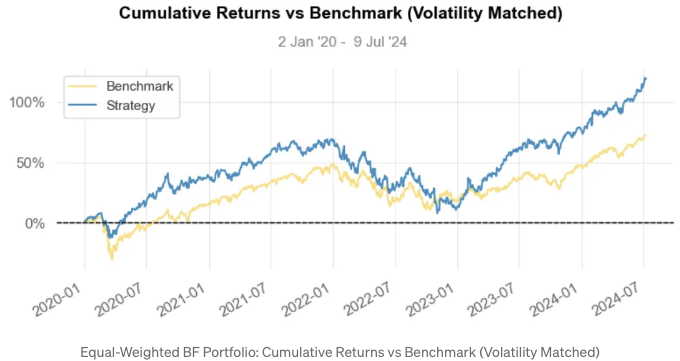
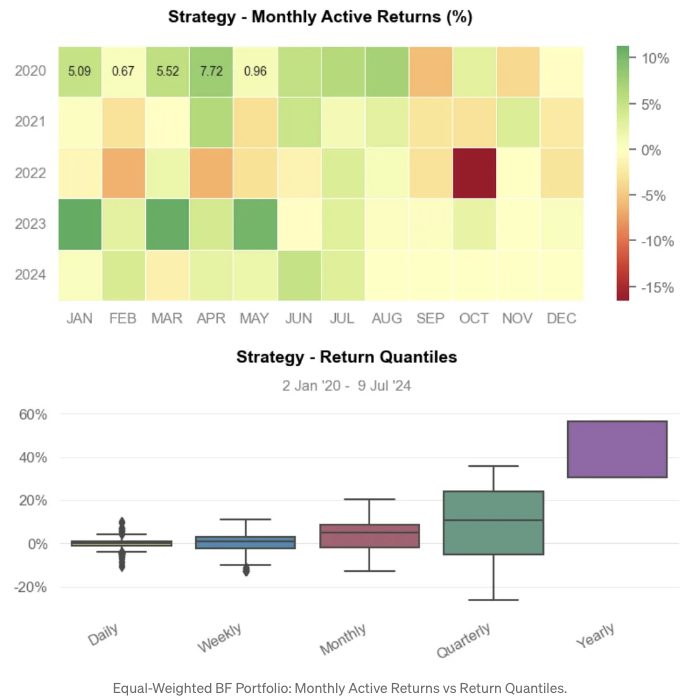
• 결과:

• 전략 누적 수익률은 약 200%에 비해 벤치마크는 약 75%입니다.

• 전략 누적 수익률(변동성 매칭)은 약 125%입니다.

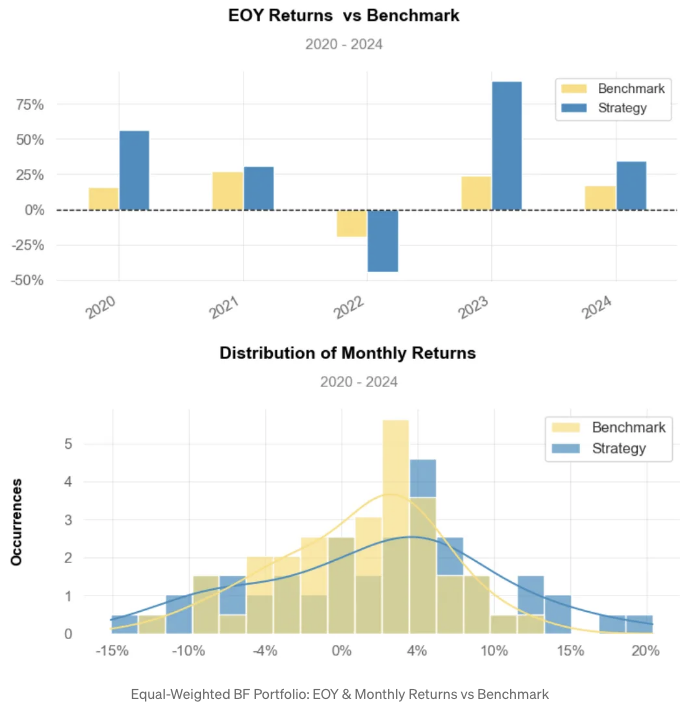
• 연말 전략 수익률은 약 30%에 비해 벤치마크는 약 15%입니다.

• 월간 수익률 분포: 전략은 약 5%에 비해 벤치마크는 약 3%입니다.

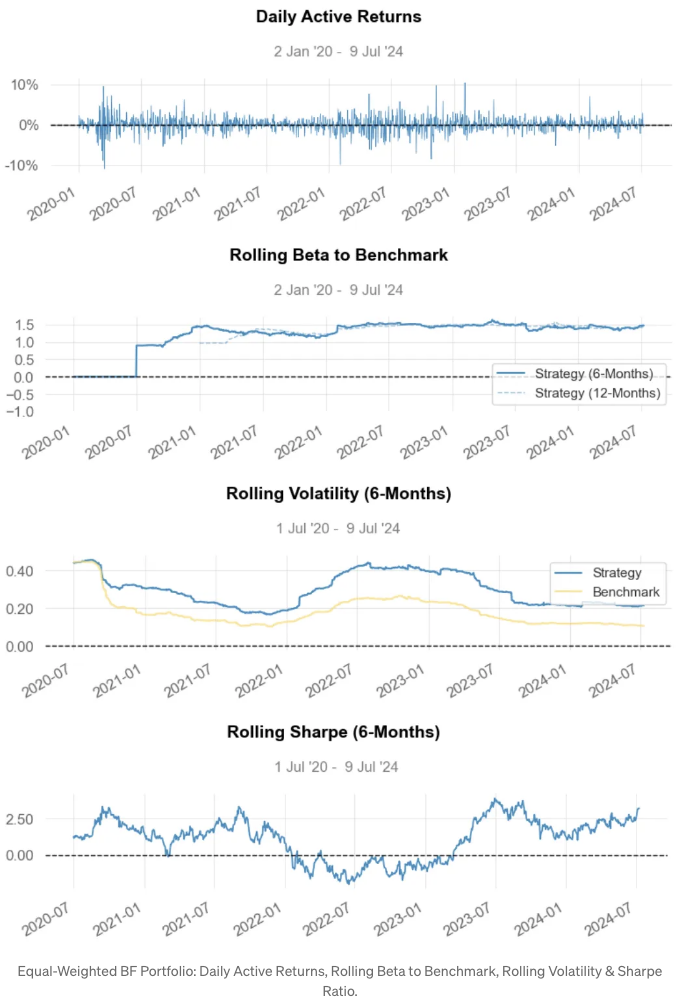
• 롤링 베타는 약 1.5입니다.

• 롤링 변동성은 약 0.2에 비해 벤치마크는 약 0.1입니다.

• 롤링 샤프 비율은 약 2.5입니다.

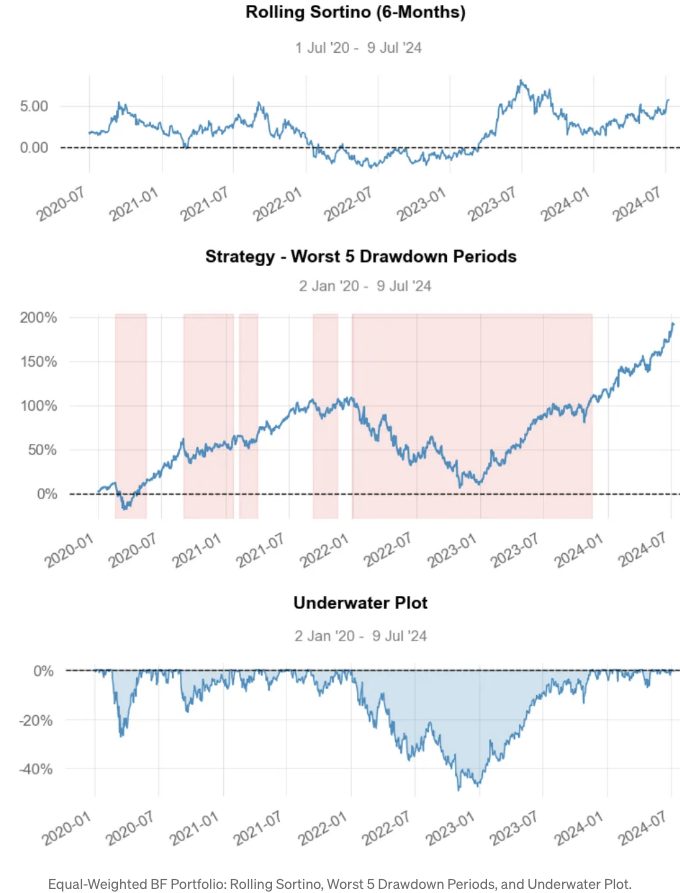
• 롤링 소르티노 비율은 약 5.0입니다.

• 최악의 손실액은 2021년 12월 28일에 -47%입니다.

• 월간 최소 활동 수익률은 2022년 10월에 -15%입니다.

• 전략 수익률 분위: 분기별으로 약 10% 및 연간으로 약 45%입니다.

• 전략의 누적 수익률 및 샤프 비율이 벤치마크보다 높아, 같은 위험 수준에 더 나은 수익을 창출한다는 것을 보여줍니다.

• 일반적으로 샤프 비율이 1.0보다 크면 투자자들에게 만족스럽거나 양호한 것으로 간주됩니다. 2.0보다 높은 비율은 매우 우수하다고 평가됩니다. 전략의 샤프 비율은 약 2.5입니다.

• 소르티노 비율은 2 이상이면 이상적인 것으로 간주됩니다. 우리의 전략은 약 5.0의 소르티노 비율을 얻습니다.

• 베타가 1보다 큰 경우: 베타가 1.0보다 크면 해당 자산의 가격이 이론적으로 시장보다 더 변동적임을 나타냅니다. 주식의 베타가 1.2면 시장보다 20% 더 변동적이라고 가정됩니다 (롤링 변동성 vs 벤치마크 비교). 테크놀로지 주식은 주요 벤치마크보다 더 높은 베타 값을 갖는 경향이 있습니다.

• 전반적으로 제안된 Equal-Weighted BF Portfolio는 합리적인 투자 수익률을 창출했지만 SPY에 비해 더 높은 변동성을 동반합니다.

BF의 최대 샤프 비율을 위한 효율적 투자 가장자리

• PyPortfolioOpt 라이브러리는 EfficientFrontier 클래스를 제공하며, 이 클래스는 공분산 행렬과 예상 수익을 입력으로 사용합니다. weights 변수는 최대 샤프 비율을 갖는 목표에 따라 각 자산에 대한 최적화된 가중치를 저장합니다.
• 효율적인 투자 가장자리(Point of Origin)를 위한 라이브러리 가져오기 및 주식 데이터 읽기.

# 포트폴리오 최적화를 위한 라이브러리 가져오기
from pypfopt.efficient_frontier import EfficientFrontier
from pypfopt import risk_models
from pypfopt import expected_returns

df=yf.download(tickers, start = '2020-01-01')['Adj Close']
df.tail()

Ticker     AAPL       AMZN       GOOG       META
Date    
2024-07-02 220.270004 200.000000 186.610001 509.500000
2024-07-03 221.550003 197.589996 187.389999 509.959991
2024-07-05 226.339996 200.000000 191.960007 539.909973
2024-07-08 227.820007 199.289993 190.479996 529.320007
2024-07-09 228.679993 199.339996 190.440002 530.000000

• 연간화된 기대수익률 및 연간 샘플 공분산 행렬을 계산하고 플로팅합니다.

# 연간화된 기대수익률 및 연간 샘플 공분산 행렬 계산
mu = expected_returns.mean_historical_return(df) # 기대 수익률
S = risk_models.sample_cov(df) # 공분산 행렬

# 연간화된 기대수익률 시각화
mu

Ticker
AAPL    0.288713
AMZN    0.179139
GOOG    0.255711
META    0.229041
dtype: float64

mu.plot.bar(label='연간화된 기대수익률')
plt.legend()

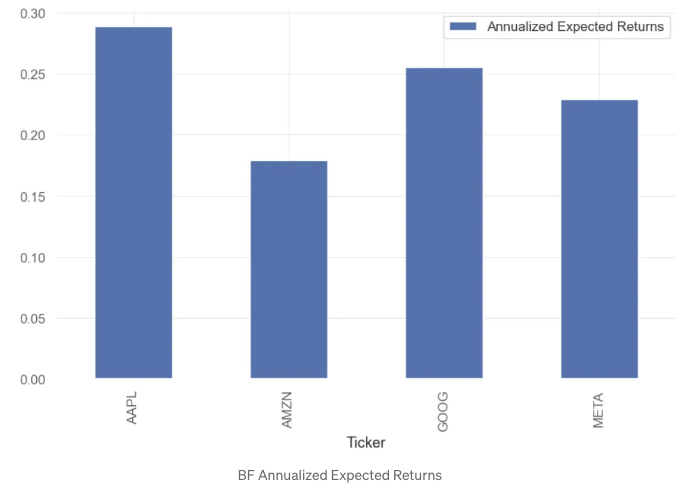
• 공분산 행렬 시각화

# 공분산 행렬 시각화
S

|        | AAPL    | AMZN    | GOOG    | META    |
|--------|---------|---------|---------|---------|
| AAPL   | 0.106707| 0.071803| 0.070835| 0.086041|
| AMZN   | 0.071803| 0.132787| 0.078590| 0.103355|
| GOOG   | 0.070835| 0.078590| 0.107778| 0.098501|
| META   | 0.086041| 0.103355| 0.098501| 0.213837|

S.style.background_gradient(cmap='coolwarm')

• MSR에 대한 포트폴리오 최적화

# 최대 샤프 비율을 위한 최적화
ef = EfficientFrontier(mu, S) # 기대수익과 공분산 행렬을 입력으로 제공
weights = ef.max_sharpe() # 샤프 비율 최적화를 위한 가중치 최적화

clean_weights = ef.clean_weights() # clean_weights는 가중치를 반올림하고 거의 0에 가까운 값을 잘라냄

# 최적화된 가중치와 포트폴리오의 예상 수익을 출력
clean_weights

OrderedDict([('AAPL', 0.66721),
             ('AMZN', 0.0),
             ('GOOG', 0.33279),
             ('META', 0.0)])

• MSR 최적화 포트폴리오 생성

# 최적화된 가중치를 사용하여 새로운 포트폴리오 생성
new_weights = [0.66721, 0.33279]
optimized_portfolio = df['AAPL']*new_weights[0] + df['GOOG']*new_weights[1]
optimized_portfolio # 일일 수익 시각화

Date
2020-01-02     71.406448
2020-01-03     70.821647
2020-01-06     71.763386
2020-01-07     71.520408
2020-01-08     72.480875
                 ...    
2024-07-02    209.068292
2024-07-03    210.181895
2024-07-05    214.898680
2024-07-08    215.393625
2024-07-09    215.954106
Length: 1136, dtype: float64

• MSR 누적 수익 시각화

optimized_portfolio.plot(label='최적화된 포트폴리오')
plt.legend()

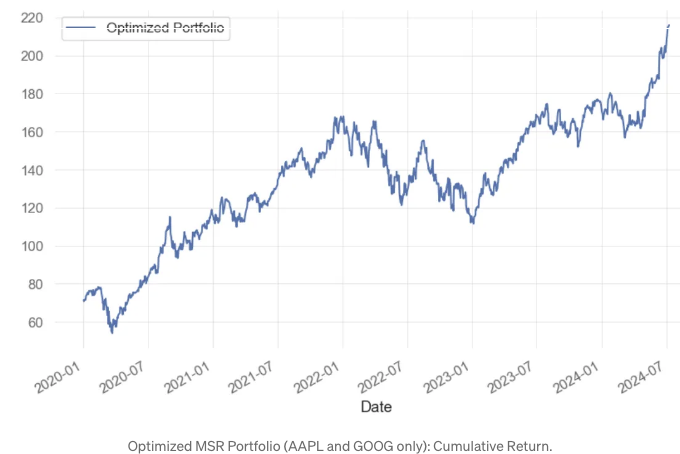
• MSR PO는 BF 대신 AAPL과 GOOG (총 2개 자산)만 고려하여 220%의 수익을 제공합니다. 이는 B2로 불리며 페어 트레이딩의 잠재적 후보입니다.
• MSR B2 포트폴리오 성과 보고서 및 전략 시각화를 SPY 벤치마크 대비 생성

# 첫 번째 포트폴리오와 최적화된 포트폴리오를 비교하는 새로운 보고서 표시
qs.reports.full(optimized_portfolio, benchmark=portfolio)

성과 지표
                           벤치마크    전략
-------------------------  -----------  ----------
시작 기간               2020-01-03   2020-01-03
종료 기간                 2024-07-09   2024-07-09
무위험 이자율             0.0%         0.0%
시장 참여 시간           100.0%       100.0%

누적 수익            184.73%      202.43%
CAGR﹪           17.34%       18.43%

샤프                     0.9          0.96
확률적인 샤프 비율         97.08%       97.9%
스마트 샤프               0.79         0.84
소르티노                    1.29         1.4
스마트 소르티노              1.13         1.23
소르티노/√2                 0.91         0.99
스마트 소르티노/√2           0.8          0.87
오메가                      1.19         1.19

최대 손실                 -49.12%      -33.58%
최장 연속 손실 일수            690          542
변동성 (연간)          31.42%       30.32%
R^2                        0.8          0.8
정보 비율                  0.0          0.0
칼마르                     0.35         0.55
외도                       -0.14        -0.07
첨도                      4.02         4.66

기대되는 일일 %           0.09%        0.1%
기대되는 월간 %         1.92%        2.03%
기대되는 연간 %          23.28%       24.77%
켈리 기준                   5.11%        8.13%
파산 위험                0.0%         0.0%
일일 가치위험            -3.14%       -3.03%
기대되는 실패(조건부 VaR)   -3.14%       -3.03%

연속 최대 성공 수          8            11
연속 최대 손실 수          6            6
이익/손실 비율           0.17         0.19
이익/손실 (1M)            1.1          1.14

상환 비율                 0.95         0.98
이익 요소               1.17         1.19
상식적인 비율           1.14         1.16
CPC 지수                0.6          0.63
꼬리 비율                0.97         0.98
이상치 이기는 비율        3.8          3.97
이상치 손실 비율         3.55         3.62

월말 이익                  5.18%        7.14%
3개월간                   16.73%       31.57%
6개월간                   36.32%       26.89%
YTD                      34.8%        23.43%
1년                    54.69%       29.71%
3년 (연간)             9.97%        10.51%
5년 (연간)             17.34%       18.43%
10년 (연간)            17.34%       18.43%
최고치 (연간)           17.34%       18.43%

최고 수익 날짜         10.41%       11.17%
최악의 날              -10.9%       -12.32%
최고의 월              20.41%       18.65%
최악의 월             -15.13%      -12.31%
최고의 연도           91.38%       62.29%
최악의 연도          -44.71%      -29.98%

평균 하락                 -3.59%       -4.0%
평균 하락 일수            23           26
회복 요인                  2.58         3.91
울서 지수                  0.18         0.12
평온 지수                   0.42         0.94

평균 상승 월              7.75%        8.26%
평균 하락 월           -6.91%       -6.96%
이익 일 %                 53.66%       54.54%
이익 월 %                65.45%       58.18%
이익 분기 %             68.42%       57.89%
이익 연도 %              80.0%        80.0%

베타                       -            0.86
알파                      -            0.05
상관 관계                -            89.32%
트레이너 비율              -            234.87%
없음

• 최악의 5번의 Drawdown

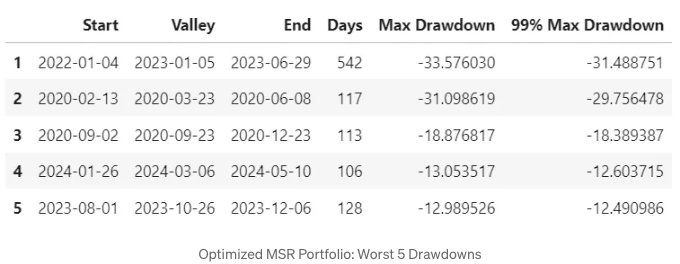
• MSR PO 전략 시각화

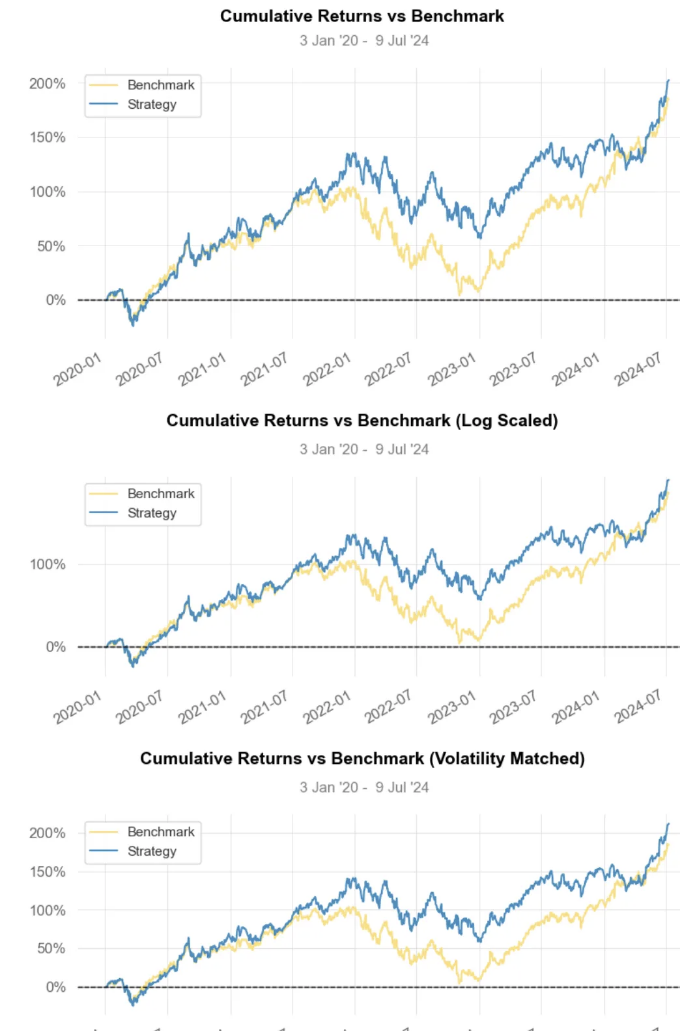
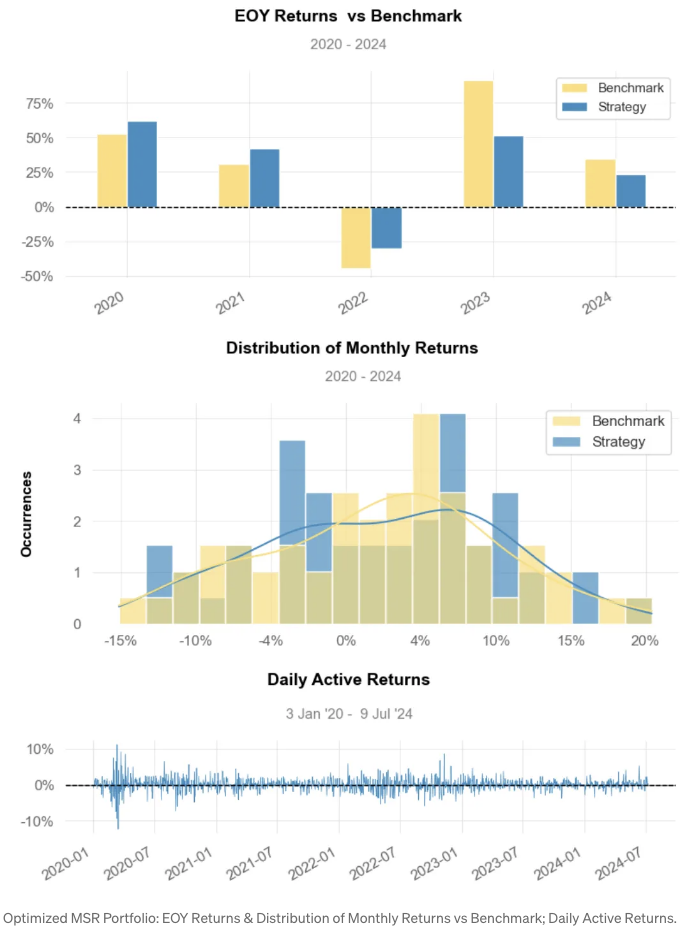
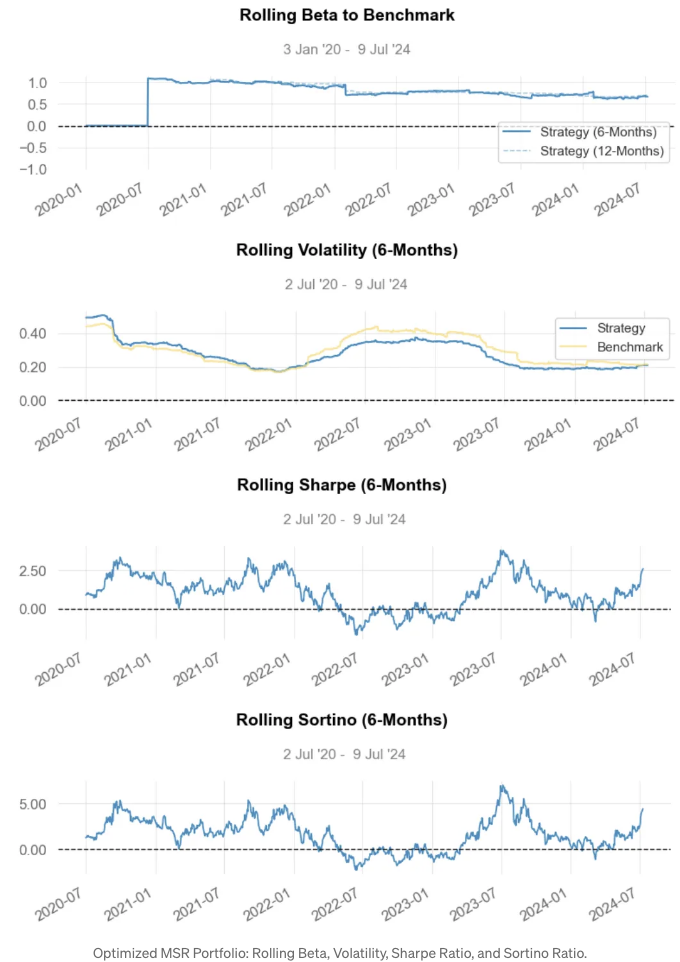
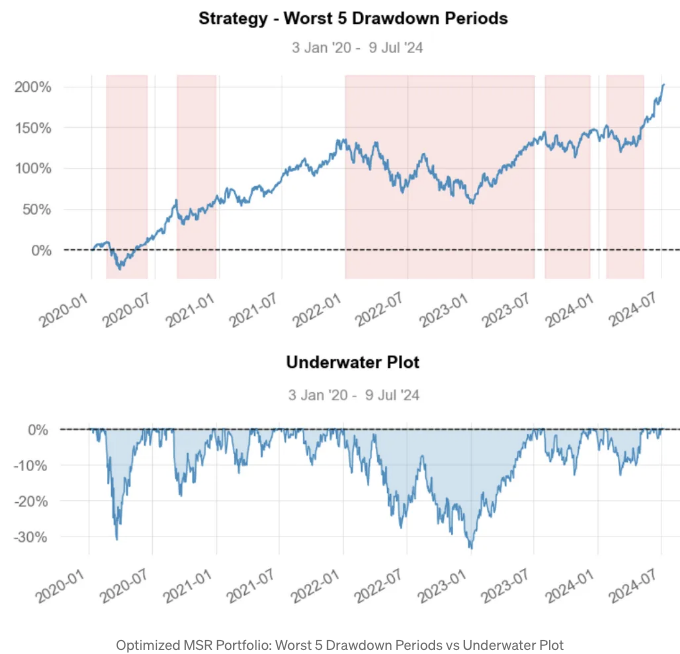
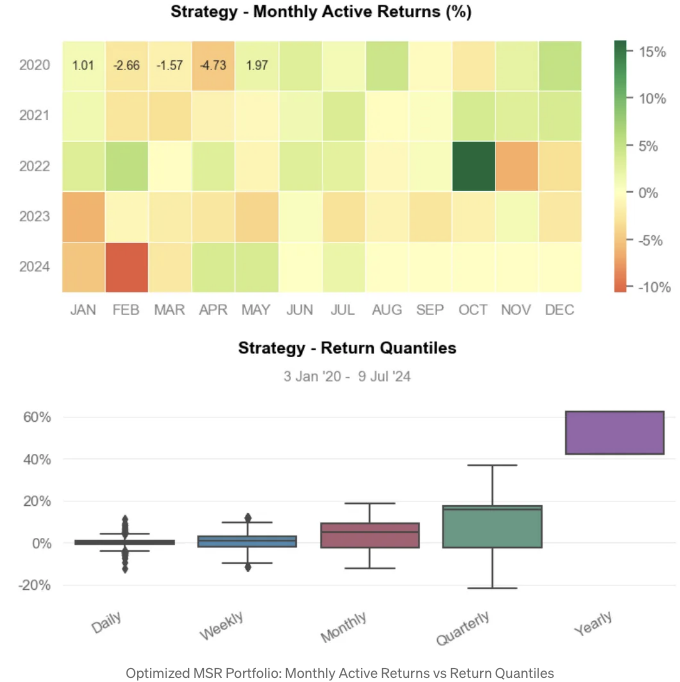
• 결론:

• 전략 누적 수익률 약 220%.

• 전략 누적 수익률 (변동성 일치) 약 210%.

• 월별 수익 분포: 전략 약 7% 대 벤치마크 약 3%.

• 롤링 베타 약 0.6

• 롤링 변동성 약 0.2

• 롤링 샤프 비율 약 2.5

• 롤링 소티노 비율 약 5.0

• 최대 손실 약 -31% (2021년 01월 04일)

• 최소 월간 순활 수익 약 -10% (2022년 10월)

• 전략 수익 분위 수: 분기별로 약 10%, 연간으로 약 50%.

• 전략의 누적 수익률과 샤프 비율이 벤치마크보다 높음을 보여줍니다. 이는 더 많은 수익을 가져오지만, 같은 수준의 위험을 감수하고 있음을 의미합니다.

• 베타 값이 1보다 낮다는 것은 MSR B2가 전체 시장보다 덜 변동성이 있다는 것을 의미합니다.

• 전반적으로 최적화된 MSR B2 포트폴리오는 위험-수익 교환 관계 측면에서 50% BF-to-B2 포트폴리오 비용 절감까지 고려하여 평등가중 BF 포트폴리오보다 우수한 성과를 거뒀습니다.

(NVDA, AMD) 대 S&P 500 수익성 분석

• FinanceToolkit [9]를 사용하여 (NVDA, AMD) 대 S&P 500 수익 분석의 세부 정보를 살펴보겠습니다.
• 입력한 과거 데이터, 손익 계산서, 수익성 비율, FA 및 TA 지표 가져오기 [9]

import matplotlib.pyplot as plt
import matplotlib.ticker as mtick
import pandas as pd
import seaborn as sns
from matplotlib import patheffects

from financetoolkit import Toolkit

API_KEY = "YOUR API KEY"

companies = Toolkit(["NVDA", "AMD"], api_key=API_KEY, start_date="2017-12-31")

# 손익 계산서
historical_data = companies.get_historical_data()

# 재무 제표 예시
income_statement = companies.get_income_statement()

# 수익성 비율
profitability_ratios = companies.ratios.collect_profitability_ratios()

# 그리스 금융 지표
all_greeks = companies.options.collect_all_greeks(expiration_time_range=180)


# 요소 자산 상관 관계
factor_asset_correlations = companies.performance.get_factor_asset_correlations(
    period="quarterly"
)

# VaR
value_at_risk = companies.risk.get_value_at_risk(period="weekly")

# TA 지표
ichimoku_cloud = companies.technicals.get_ichimoku_cloud()

누적 수익률

• NVDA, AMD 및 S&P 500의 누적 수익률을 시각화합니다. [9]

display(역사적_데이터)

# 클립 보드에 복사 (이건 README에 데이터를 붙여 넣기 위함입니다)
pd.io.clipboards.to_clipboard(
    역사적_데이터.xs("NVDA", axis=1, level=1).iloc[:-1].head().to_markdown(),
    excel=False,
)

# 누적 수익을 위한 라인 차트 생성
ax = 역사적_데이터["누적 수익"].plot(
    figsize=(15, 5),
    lw=2,
)

# 색상 및 라인 스타일 사용자 정의
ax.set_prop_cycle(color=["#007ACC", "#FF6F61", "#4CAF50"])
ax.set_xlabel("년도")
ax.set_ylabel("누적 수익")
ax.set_title(
    "NVDA 및 AMD의 누적 수익과 S&P 500을 벤치마크로 함께한 수익"
)

# 범례 추가
ax.legend(["NVDA", "AMD", "S&P 500"], loc="upper left")

# 가시성을 위해 그리드 라인 추가
ax.grid(True, linestyle="--", alpha=0.7)

plt.show()

변동성

• NVDA 및 AMD 대 S&P 500의 변동성 그래픽화

print(historical_data['Volatility'].iloc[-1])
NVDA        0.0324
AMD         0.0345
Benchmark   0.0125
Name: 2024-07-09, dtype: float64

historical_data['Volatility'].iloc[-1].plot.bar(title='Volatility')

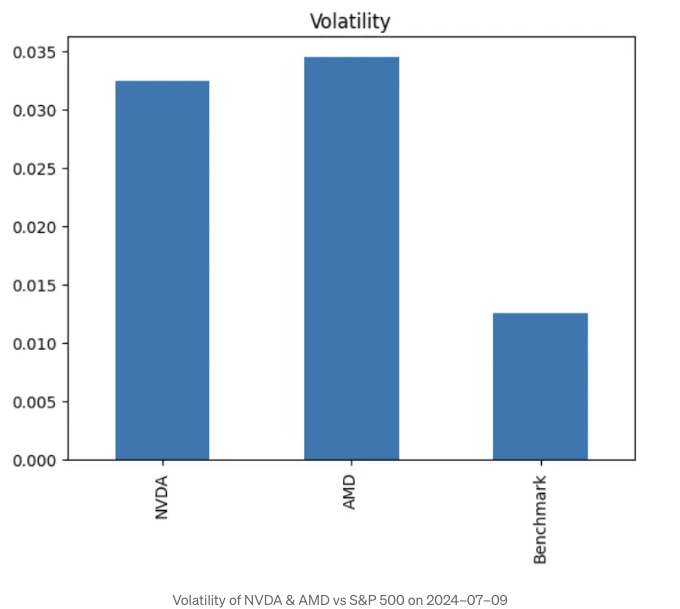
• 저희 두 자산의 변동성이 벤치마크의 3배 정도 더 높다는 것을 알 수 있습니다.

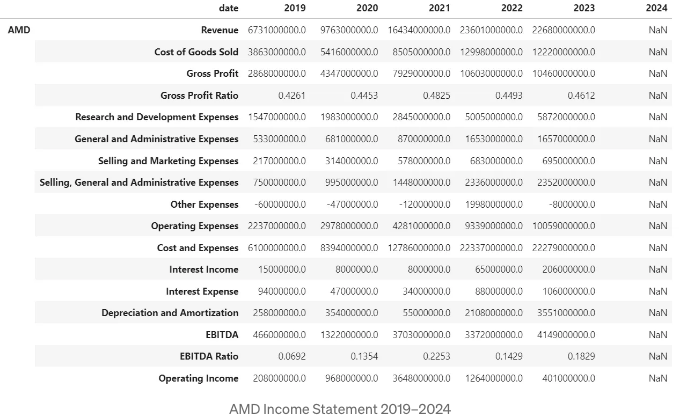
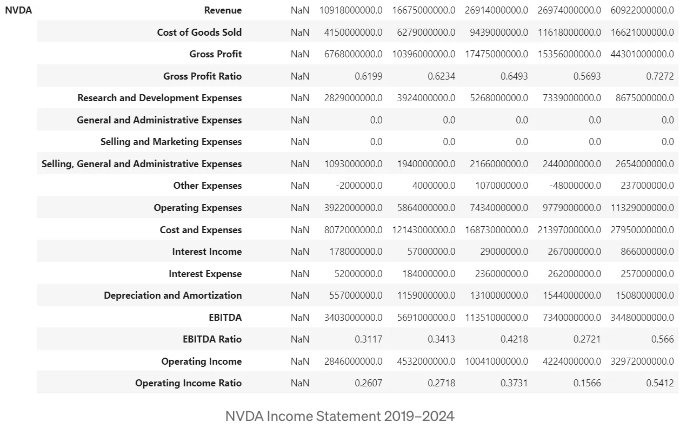
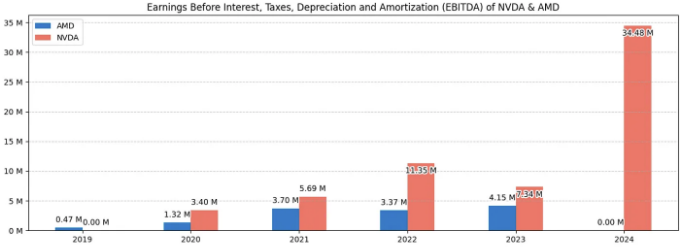
손익계산서

• 2019년부터 2024년까지의 NVDA 및 AMD 손익 계산서를 비교해보세요 [9]

income_statement를 출력하세요

# 클립보드에 복사하세요 (README에 데이터를 붙여넣기 위한 용도입니다)
pd.io.clipboards.to_clipboard(
    income_statement.loc["NVDA"].head().to_markdown(), excel=False
)

# 막대 그래프 생성
ebitda_data = income_statement.loc[:, "EBITDA", :].T
colors = ["#007ACC", "#FF6F61"]
ax = ebitda_data.plot.bar(figsize=(15, 5), color=colors)

# 막대 위에 데이터 라벨 추가 (백만으로 나누어 사용자 정의 포맷팅 (백만과 천 단위 구분))
for p in ax.patches:
    ebitda_millions = p.get_height() / 1_000_000_000
    label = f"{ebitda_millions:,.2f} M"
    x = p.get_x() + p.get_width() / 2.0
    y = p.get_height()

    # 라벨이 차트 상단과 너무 가까운지 확인
    if y < 0.2 * ax.get_ylim()[1]:
        va = "bottom"
        xytext = (0, 5)
    else:
        va = "top"
        xytext = (0, -5)

    # 텍스트에 대한 스트로크 효과 생성
    text = ax.annotate(
        label,
        (x, y),
        ha="center",
        va=va,
        fontsize=10,
        color="black",
        xytext=xytext,
        textcoords="offset points",
    )
    text.set_path_effects([patheffects.withStroke(linewidth=3, foreground="white")])

# 축 라벨 사용자 정의
plt.xlabel("", fontsize=10)
plt.ylabel("", fontsize=10)

# x tick의 각도 조정
plt.xticks(rotation=0)

# 제목 설정
plt.title(
    "Earnings Before Interest, Taxes, Depreciation and Amortization (EBITDA) of NVDA & AMD",
    fontsize=12,
)

# 명확성을 위해 수평 grid 추가
plt.grid(axis="y", linestyle="--", alpha=0.7)

# y축에 천 단위 구분 추가
ax.yaxis.set_major_formatter(
    mtick.FuncFormatter(lambda x, _: f"{x / 1_000_000_000:,.0f} M")
)

# 그래프 출력
plt.show()

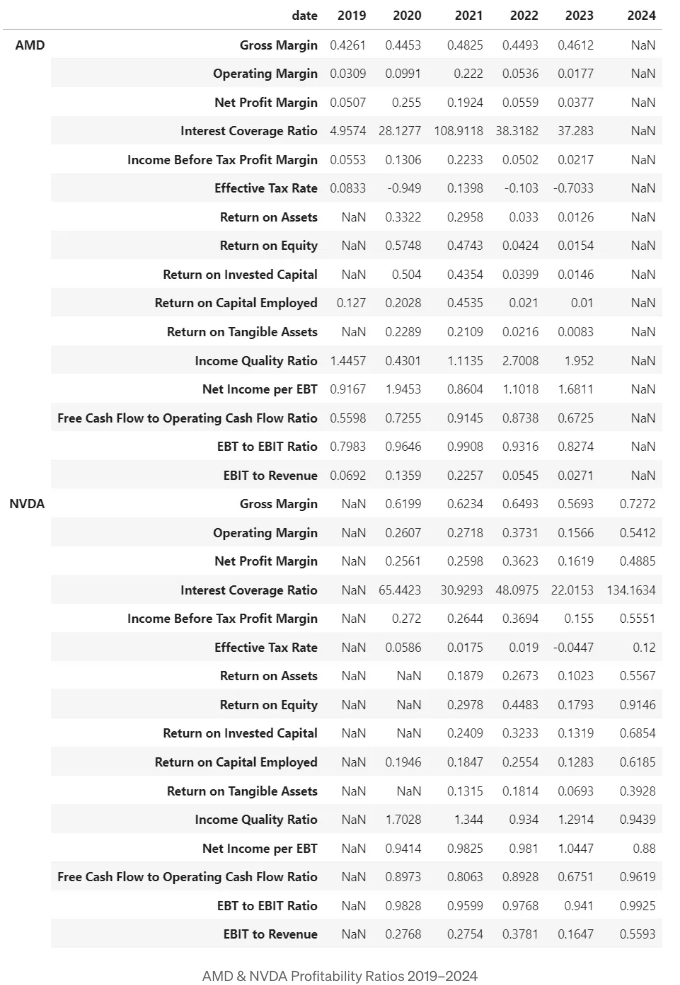
수익성 비율

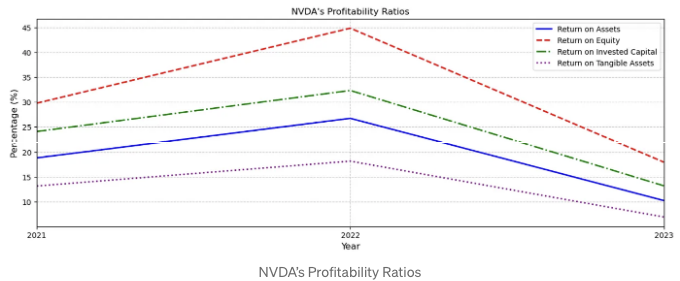
• NVDA 및 AMD 수익성 비율 2019–2024 시각화 [9]

display(profitability_ratios)

# 클립 보드로 복사 (이것은 README에 데이터를 붙여넣기하기 위한 것입니다)
pd.io.clipboards.to_clipboard(
    profitability_ratios.loc["NVDA"].head().to_markdown(), excel=False
)

ratios_to_plot = [
    "Return on Assets",
    "Return on Equity",
    "Return on Invested Capital",
    "Return on Tangible Assets",
]

# 그림 생성
ax = (
    (profitability_ratios.dropna(axis=1) * 100)
    .loc["NVDA", ratios_to_plot, :]
    .T.plot(figsize=(15, 5), title="NVDA의 수익성 비율", lw=2)
)

# 라인 스타일과 색상 커스터마이징
line_styles = ["-", "--", "-.", ":"]
line_colors = ["blue", "red", "green", "purple"]
for i, line in enumerate(ax.get_lines()):
    line.set_linestyle(line_styles[i])
    line.set_color(line_colors[i])

# 범례 커스터마이징
ax.legend(ratios_to_plot)

# 라벨 및 그리드 추가
plt.xlabel("Year", fontsize=12)
plt.ylabel("Percentage (%)", fontsize=12)
plt.grid(True, linestyle="--", alpha=0.7)

# 제목 커스터마이징
plt.title("NVDA의 수익성 비율")

# 그림 표시
plt.show()

-md

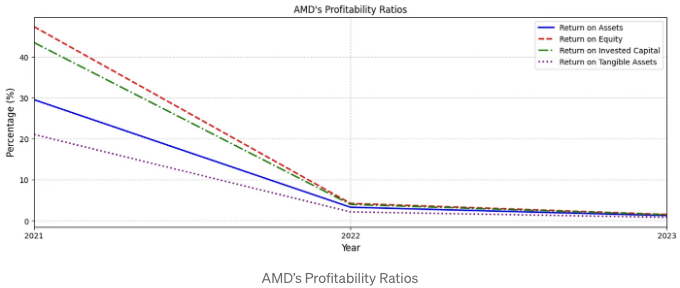
• AMD 수익성 비율 그래픽 그리기

# 클립 보드로 복사 (README에 데이터를 붙여넣을 때 사용)
pd.io.clipboards.to_clipboard(
    profitability_ratios.loc["AMD"].head().to_markdown(), excel=False
)

ratios_to_plot = [
    "Return on Assets",
    "Return on Equity",
    "Return on Invested Capital",
    "Return on Tangible Assets",
]

# 그림 생성
ax = (
    (profitability_ratios.dropna(axis=1) * 100)
    .loc["AMD", ratios_to_plot, :]
    .T.plot(figsize=(15, 5), title="AMD의 수익성 비율", lw=2)
)

# 라인 스타일과 색상 사용자 정의
line_styles = ["-", "--", "-.", ":"]
line_colors = ["blue", "red", "green", "purple"]
for i, line in enumerate(ax.get_lines()):
    line.set_linestyle(line_styles[i])
    line.set_color(line_colors[i])

# 범례 사용자 정의
ax.legend(ratios_to_plot)

# 레이블과 그리드 추가
plt.xlabel("년도", fontsize=12)
plt.ylabel("백분율 (%)", fontsize=12)
plt.grid(True, linestyle="--", alpha=0.7)

# 제목 사용자 정의
plt.title("AMD의 수익성 비율")

# 그림 표시
plt.show()

• 2023년 NVDA 대 AMD 수익성 비율 검토

print(profitability_ratios['2023'])

AMD   매출 이익율                                     0.4612
      영업 이익율                                   0.0177
      순이익율                                      0.0377
      이자 상환 여유성 비율                           37.283
      세전 순이익 마진                              0.0217
      유효 세율                                   -0.7033
      자산 수익률                                   0.0126
      자본 수익률                                   0.0154
      투자 자본 이익률                             0.0146
      자본 운용 이익률                               0.01
      유형 자산 수익률                             0.0083
      소득 품질 비율                               1.952
      EBT당 순이익                                1.6811
      영업현금흐름 대 영업 현금흐름 비율           0.6725
      EBT 대 EBIT 비율                           0.8274
      EBIT 대 매출                               0.0271
NVDA  매출 이익율                                    0.5693
      영업 이익율                                   0.1566
      순이익율                                      0.1619
      이자 상환 여유성 비율                        22.0153
      세전 순이익 마진                             0.155
      유효 세율                                  -0.0447
      자산 수익률                                   0.1023
      자본 수익률                                   0.1793
      투자 자본 이익률                            0.1319
      자본 운용 이익률                            0.1283
      유형 자산 수익률                            0.0693
      소득 품질 비율                              1.2914
      EBT당 순이익                               1.0447
      영업현금흐름 대 영업 현금흐름 비율           0.6751
      EBT 대 EBIT 비율                           0.941
      EBIT 대 매출                               0.1647
Name: 2023, dtype: float64

plt.figure(figsize=(14, 8))
prof=profitability_ratios['2023']
cols = ['NVDA', 'AMD']
prof[cols].plot(kind='bar')

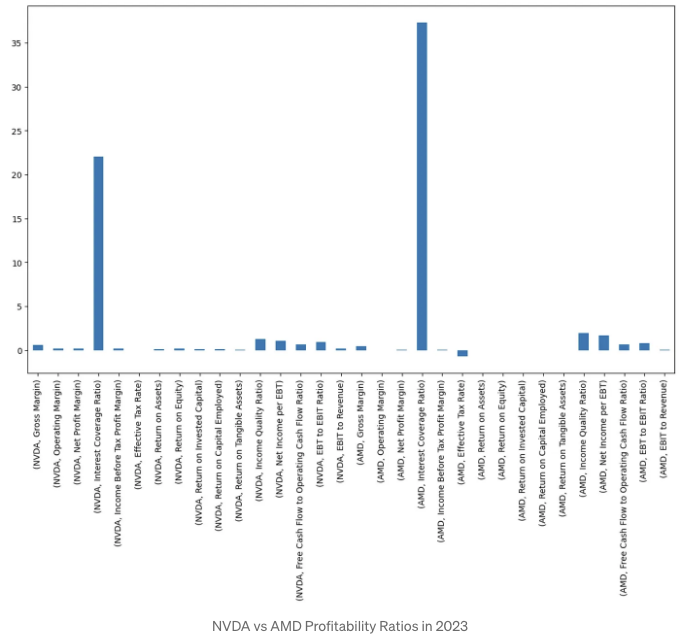
• 2023년 NVDA 대 AMD 수익성 비율 확대

plt.figure(figsize=(14, 8))
prof = profitability_ratios['2023']
cols = ['NVDA', 'AMD']
prof[cols].plot(kind='bar')
plt.ylim(-1, 2.5)

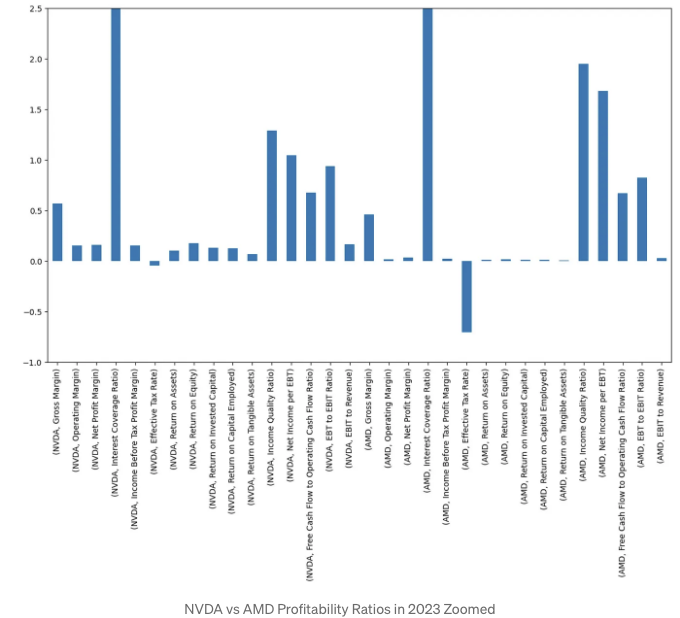
AMD 대 NVDA 그리스 민감도

• AMD에 대한 그리스 감수치 분석 중 [9]

import matplotlib.pyplot as plt
from matplotlib import cm

fig, ax = plt.subplots(figsize=(15, 10), ncols=2, nrows=2)

delta_over_time_df = pd.DataFrame()
dates = all_greeks.columns.get_level_values(0)

# 1, 2개월 ... 처리
for i, time in enumerate(range(30, 210, 30)):

    try:
        period_column = dates[time]
    except IndexError:
        period_column = dates[-1]

    color = cm.viridis(i / 5)  # 색상 변화에 viridis colormap 사용

    # Delta plot
    ax[0, 0].plot(all_greeks.loc["AMD", (period_column, "Delta")], color=color)

    # Gamma plot
    ax[0, 1].plot(all_greeks.loc["AMD", (period_column, "Gamma")], color=color)

    # Theta plot
    ax[1, 0].plot(all_greeks.loc["AMD", (period_column, "Theta")], color=color)

    # Vega plot
    ax[1, 1].plot(all_greeks.loc["AMD", (period_column, "Vega")], color=color)

    delta_over_time_df = pd.concat(
        [delta_over_time_df, all_greeks.loc["AMD", (period_column, "Delta")]], axis=1
    )

date_labels = [
    "1 달",
    "2 달",
    "3 달",
    "4 달",
    "5 달",
    "6 달",
]

delta_over_time_df.columns = date_labels

# DataFrame 표시
display(delta_over_time_df.iloc[7:12])

# 클립보드로 복사 (README에 데이터를 붙여넣으려면)
pd.io.clipboards.to_clipboard(delta_over_time_df.iloc[7:12].to_markdown(), excel=False)

# 타이틀 및 레이블
for number1, number2 in [(0, 0), (1, 0), (0, 1), (1, 1)]:
    ax[number1, number2].set_xlim(
        [all_greeks.loc["AMD"].index.min(), all_greeks.loc["AMD"].index.max()]
    )
    ax[number1, number2].grid(True, linestyle="--", alpha=0.7)
    ax[number1, number2].set_xlabel("행사가")
    ax[number1, number2].set_facecolor("#F5F5F5")

ax[0, 0].set_title("Delta")
ax[0, 1].set_title("Gamma")
ax[1, 0].set_title("Theta")
ax[1, 1].set_title("Vega")

# 레이아웃 조정
fig.legend(
    date_labels,
    loc="upper center",
    ncol=6,
    bbox_to_anchor=(0.5, 0),
    frameon=False,
)
fig.suptitle(
    "AMD에 대한 그리스 감수치 분석", fontsize=30, x=0.5, y=0.98, fontfamily="cursive"
)

fig.tight_layout()

# 플롯 표시
plt.show()

    1 달 2 달 3 달 4 달 5 달 6 달
165 0.872 0.8067 0.7692 0.7398 0.7236 0.7113
170 0.7487 0.698 0.6728 0.6544 0.6449 0.638
175 0.5863 0.5721 0.5664 0.5631 0.562 0.5615
180 0.4124 0.442 0.458 0.471 0.4786 0.4848
185 0.2582 0.3212 0.3555 0.3828 0.3985 0.4108

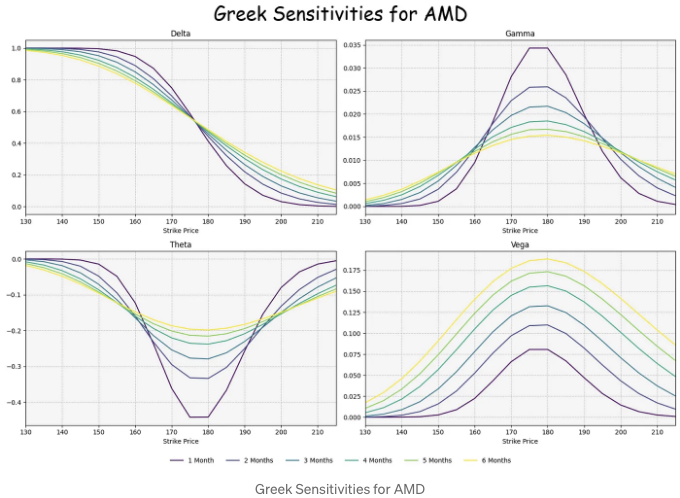
• NVDA에 대한 그리스 감수치 분석 중 [9]

import matplotlib.pyplot as plt
from matplotlib import cm

fig, ax = plt.subplots(figsize=(15, 10), ncols=2, nrows=2)

delta_over_time_df = pd.DataFrame()
dates = all_greeks.columns.get_level_values(0)

# Loop through different times
for i, time in enumerate(range(30, 210, 30)):

    try:
        period_column = dates[time]
    except IndexError:
        period_column = dates[-1]

    color = cm.viridis(i / 5)  # Using viridis colormap for color variation

    # Delta plot
    ax[0, 0].plot(all_greeks.loc["NVDA", (period_column, "Delta")], color=color)

    # Gamma plot
    ax[0, 1].plot(all_greeks.loc["NVDA", (period_column, "Gamma")], color=color)

    # Theta plot
    ax[1, 0].plot(all_greeks.loc["NVDA", (period_column, "Theta")], color=color)

    # Vega plot
    ax[1, 1].plot(all_greeks.loc["NVDA", (period_column, "Vega")], color=color)

    delta_over_time_df = pd.concat(
        [delta_over_time_df, all_greeks.loc["NVDA", (period_column, "Delta")]], axis=1
    )

date_labels = [
    "1 Month",
    "2 Months",
    "3 Months",
    "4 Months",
    "5 Months",
    "6 Months",
]

delta_over_time_df.columns = date_labels

# Show the DataFrame
display(delta_over_time_df.iloc[7:12])

# Copy to clipboard (this is just to paste the data in the README)
pd.io.clipboards.to_clipboard(delta_over_time_df.iloc[7:12].to_markdown(), excel=False)

# Titles and labels
for number1, number2 in [(0, 0), (1, 0), (0, 1), (1, 1)]:
    ax[number1, number2].set_xlim(
        [all_greeks.loc["NVDA"].index.min(), all_greeks.loc["NVDA"].index.max()]
    )
    ax[number1, number2].grid(True, linestyle="--", alpha=0.7)
    ax[number1, number2].set_xlabel("Strike Price")
    ax[number1, number2].set_facecolor("#F5F5F5")

ax[0, 0].set_title("Delta")
ax[0, 1].set_title("Gamma")
ax[1, 0].set_title("Theta")
ax[1, 1].set_title("Vega")

# Adjust layout
fig.legend(
    date_labels,
    loc="upper center",
    ncol=6,
    bbox_to_anchor=(0.5, 0),
    frameon=False,
)
fig.suptitle(
    "Greek Sensitivities for NVDA", fontsize=30, x=0.5, y=0.98, fontfamily="cursive"
)

fig.tight_layout()

# Show the plot
plt.show()

    1 Month 2 Months 3 Months 4 Months 5 Months 6 Months
135 0.3367 0.3835 0.4084 0.4282 0.4395 0.4484
140 0.1525 0.2277 0.2722 0.3087 0.3298 0.3466
145 0.0539 0.1188 0.1666 0.2099 0.2363 0.2578
150 0.0149 0.0547 0.0939 0.1349 0.1619 0.1848
155 0.0033 0.0224 0.049 0.0822 0.1063 0.128

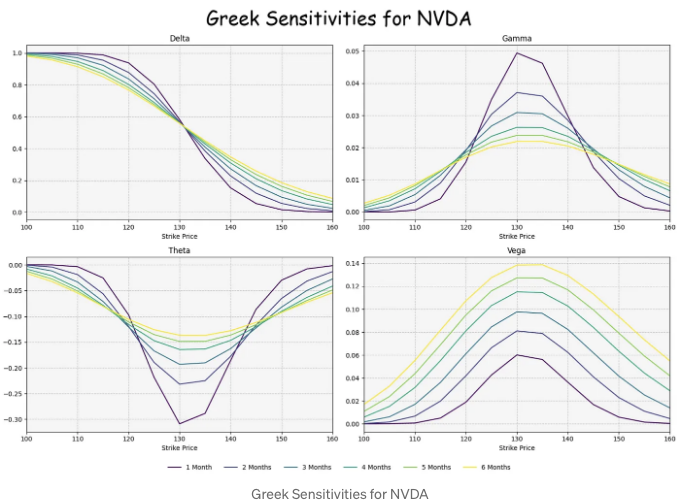
해석: 옵션 그리스는 옵션 가격이 변동성이나 기초 자산의 가격과 같은 기본 결정 요소에 대한 민감성을 나타내는 재정적 측정치입니다. 그리스는 옵션 포트폴리오를 분석하고 옵션 또는 옵션 포트폴리오의 민감성 분석에 활용됩니다. 이러한 측정치는 많은 투자자에 의해 옵션 거래에 대한 정보를 얻기 위한 필수적인 요소로 간주됩니다.

Delta: 기초 자산의 가격이 $1 증가하면 옵션의 가격이 Delta 금액만큼 변동합니다.

감마는 델타의 변화가 기초 자산 가격 변동과 어떻게 관련되는지를 측정하는 지표입니다. 기초 자산 가격이 $1 증가하면, 옵션의 델타는 감마만큼 변화합니다.

베가는 옵션의 가격이 기초 자산의 변동성에 얼마나 민감한지를 나타내는 옵션 그리스 중 하나입니다. 기초 자산의 변동성이 1% 증가하면, 옵션 가격은 베가만큼 변화합니다.

세타는 옵션 가격이 옵션의 만기까지 남은 시간에 대해 얼마나 민감한지를 나타내는 지표입니다. 옵션의 만기까지 남은 기간이 하루 줄어들면, 옵션 가격은 세타만큼 변화합니다. 세타 옵션 그리스는 시간 가치 손실이라고도 불립니다.

• ATM(At the money)은 옵션의 행사 가격이 기초 자산의 현재 시장 가격과 동일한 상황을 말합니다. ATM 콜 옵션은 델타가 0.50입니다.
• NVDA/AMD의 ATM 행사 가격 USD는 130/175입니다.
• 세타는 일반적으로 롱 포지션에 대해 음수로 표현되며, 옵션 가치의 얼마나 많은 부분이 손실되고 있는지를 나타냅니다.
• 저희의 그래프는 NVDA/AMD의 ATM 세타가 약 -0.3/-0.45임을 보여줍니다.
• 델타가 . 40-. 60 범위에 있거나 일반적으로 옵션이 ATM일 때 감마가 가장 높습니다. 따라서 만약 옵션의 델타가 +40이고 감마가 10이라면 기초 자산 가격이 1달러 오르면 그 옵션의 델타가 +50이 됩니다.
• 저희 예시에서 NVDA/AMD의 ATM 감마는 0.05/0.035입니다.
• 옵션 베가는 기본 주가 변동성에 대한 옵션의 민감도를 보고하는 것입니다. 더 높은 베가 값은 옵션 가격이 변동성 변화에 민감하다는 것을 나타내고, 더 낮은 베가는 옵션 가격이 변동성 변화에 민감하지 않다는 것을 나타냅니다.
• 우리의 다이어그램은 NVDA/AMD의 ATM 베가가 0.14/0.18임을 나타냅니다.

NVDA & AMD VaR vs Benchmark

• NVDA & AMD Value-at-Risk (VaR) vs Benchmark을 플로팅합니다. [9]

	NVDA	AMD	Benchmark
2017-01-02/2017-01-08	-0.0198	-0.0141	-0.0007
2017-01-09/2017-01-15	-0.0146	-0.0356	-0.0031
2017-01-16/2017-01-22	-0.0217	-0.0627	-0.0037
2017-01-23/2017-01-29	NaN	-0.004	-0.0024
2017-01-30/2017-02-05	-0.0131	-0.0192	-0.005
...	...	...	...
2024-06-03/2024-06-09	-0.0096	-0.0215	-0.001
2024-06-10/2024-06-16	-0.0042	-0.0376	NaN
2024-06-17/2024-06-23	-0.0349	-0.0214	-0.0025
2024-06-24/2024-06-30	-0.0573	-0.0147	-0.0038
2024-07-01/2024-07-07	-0.0079	-0.0255	NaN

2024-07 추론: NVDA, AMD 및 S&P 500의 VaR은 각각 약 5%, 3% 및 1%입니다.

NVDA 및 AMD의 Fama-French 요인과의 상관 관계

• 투자자들은 위험을 양적화하고 자본에 대한 예상 수익을 추정하는 데 사용되는 금융 모델을 찾고 있습니다. Fama French 5요인 모델은 가장 고전적인 모델 중 하나입니다(Fama 및 French, 2015).
• NVDA와 AMD의 Fama-French 요인과의 상관 관계 탐색

화면에 요소 대상 상호 상관 관계를 표시합니다.

# 클립 보드에 복사하기 (README에 데이터를 붙여넣기하려는 목적)
pd.io.clipboards.to_clipboard(
    factor_asset_correlations.xs("NVDA", axis=1, level=0)
    .iloc[:-1]
    .tail()
    .to_markdown(),
    excel=False,
)

# factor_asset_correlations DataFrame을 정의하세요 (YourDataFrame을 대체하세요)
correlations_aapl = factor_asset_correlations.xs("NVDA", axis=1, level=0)
correlations_msft = factor_asset_correlations.xs("AMD", axis=1, level=0)

# x축을 공유하며 서브플롯을 만들고 스타일을 사용자 정의하세요
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(10, 8), sharex=True)

# 선에 대한 색상 팔렛트 설정
colors = ["#007ACC", "#FF6F61", "#4CAF50", "#FFD700", "#FF6347", "#6A5ACD", "#FF8C00"]

# AAPL의 상호 상관 관계 그래프
correlations_aapl.plot(
    ax=ax1, title="NVDA의 Fama-French Factors와의 상관 관계", color=colors
)
ax1.set_ylabel("상관 관계")
ax1.legend(loc="upper right", frameon=False)

# MSFT의 상호 상관 관계 그래프
correlations_msft.plot(
    ax=ax2, title="AMD의 Fama-French Factors와의 상관 관계", color=colors
)
ax2.set_xlabel("날짜")
ax2.set_ylabel("상관 관계")
ax2.legend(loc="upper right", frameon=False)

# 명확한 그리드 선을 추가하세요
ax1.grid(True, linestyle="--", alpha=0.5)
ax2.grid(True, linestyle="--", alpha=0.5)

# 범례 및 레이블을 사용자 정의하세요
ax1.legend(loc="upper right", frameon=False)
ax2.legend(loc="upper right", frameon=False)

# 서브플롯의 배경색을 설정하세요
ax1.set_facecolor("#F9F9F9")
ax2.set_facecolor("#F9F9F9")

# 서브플롯의 위쪽과 오른쪽 테두리를 제거하세요
ax1.spines[["top", "right"]].set_visible(False)
ax2.spines[["top", "right"]].set_visible(False)

# 간격을 최적화하기 위해 tight 레이아웃 설정
plt.tight_layout()

# 그래프 보기
plt.show()

• MKT은 시장의 초과수익입니다. 이것은 가치가 가중치가 부여된 시장 포트폴리오의 수익률입니다.
• SMB는 소형 주식의 다양한 포트폴리오의 수익률에서 대형 주식의 다양한 포트폴리오의 수익률을 뺀 값입니다.
• HML은 고 Book-to-Market 비율을 가진 주식의 다양한 포트폴리오와 저 Book-to-Market 비율을 가진 주식의 다양한 포트폴리오 간의 차이입니다.
• RMW는 강한(높고 안정적인) 수익성을 가진 주식의 다양한 포트폴리오와 약한(낮은) 수익성을 가진 주식의 다양한 포트폴리오 간의 차이입니다.
• CMA는 저 및 고 투자 기업의 다양한 포트폴리오 간의 차이로 정의됩니다. 여기서 저/고 투자는 재투자 비율이 낮음/높음을 의미합니다.

추론 2024:

• HML(NVDA)`HML(AMD)
• 만약 가치 주식이 성장 주식을 능가할 것이라고 믿는다면, 포트폴리오를 HML 요인이 높은 자산 쪽으로 기울이는 것이 좋습니다.
• 우리의 예에서는 저 Book-to-Market 비율을 가진 대형기업의 경우, "큰 규모" 및 "낮은 가치" 범주로 분류됩니다. Fama-French 모델에 따르면, 이 기업은 장기적으로 낮은 수익률을 제공할 것으로 예상되며, SMB 및 HML 요인이 모두 음수일 것으로 예상됩니다.
• HML 요인과 유사하게 정의된 수익성 요인(RMW)은 운영 수익성이 강한(높음) 기업과 약한(낮은) 기업의 수익률 간의 차이입니다. 우리는 알 수 있습니다.
• RMW(NVDA) 약 0.25이며 RMW(AMD) 약 0.1입니다.

TA 이치모쿠 클라우드: NVDA 대 AMD

• TA 이치모쿠 클라우드는 시장 심리와 가격 모멘텀을 한눈에 볼 수 있게 하여 트레이더가 추세를 식별하는 데 도움을 줄 수 있습니다.
• NVDA & AMD에 대한 이치모쿠 클라우드 비교

display(ichimoku_cloud)

# 이치모쿠 클라우드 데이터 데이터프레임 정의
ichimoku_data_aapl = ichimoku_cloud.xs("NVDA", level=1, axis=1)
ichimoku_data_msft = ichimoku_cloud.xs("AMD", level=1, axis=1)

# 클립보드에 복사 (이것은 README에 데이터를 붙여넣기하기 위한 것입니다)
pd.io.clipboards.to_clipboard(ichimoku_data_aapl.tail().to_markdown(), excel=False)

# 마지막 500행 가져오기
ichimoku_data_aapl = ichimoku_data_aapl.iloc[-500:]
ichimoku_data_msft = ichimoku_data_msft.iloc[-500:]

# 수평 서브플롯을 위한 그림 및 두 개의 축 생성
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(15, 6))

# PeriodIndex를 DatetimeIndex로 변환
ichimoku_data_aapl.index = ichimoku_data_aapl.index.to_timestamp()
ichimoku_data_msft.index = ichimoku_data_msft.index.to_timestamp()

# NVDA용 이치모쿠 클라우드 플롯
ax1.plot(
    ichimoku_data_aapl.index,
    ichimoku_data_aapl["Conversion Line"],
    color="blue",
    label="Conversion Line (텐칸센)",
    linewidth=2,
)
ax1.plot(
    ichimoku_data_aapl.index,
    ichimoku_data_aapl["Base Line"],
    color="red",
    label="Base Line (기준선)",
    linewidth=2,
)
ax1.fill_between(
    ichimoku_data_aapl.index,
    ichimoku_data_aapl["Leading Span A"],
    ichimoku_data_aapl["Leading Span B"],
    where=ichimoku_data_aapl["Leading Span A"] >= ichimoku_data_aapl["Leading Span B"],
    facecolor="green",
    alpha=0.2,
    label="상승 클라우드",
)
ax1.fill_between(
    ichimoku_data_aapl.index,
    ichimoku_data_aapl["Leading Span A"],
    ichimoku_data_aapl["Leading Span B"],
    where=ichimoku_data_aapl["Leading Span A"] < ichimoku_data_aapl["Leading Span B"],
    facecolor="red",
    alpha=0.2,
    label="하락 클라우드",
)

# NVDA에 대한 범례 및 레이블 사용자 정의
ax1.legend(loc="upper left")
ax1.set_xlabel("날짜", fontsize=14)
ax1.set_ylabel("가격", fontsize=14)
ax1.set_title("이치모쿠 클라우드 차트 (NVDA)", fontsize=16)
ax1.grid(True, linestyle="--", alpha=0.5)
ax1.set_facecolor("#f7f7f7")
ax1.tick_params(axis="both", which="major", labelsize=12)

# MSFT용 이치모쿠 클라우드 플롯
ax2.plot(
    ichimoku_data_msft.index,
    ichimoku_data_msft["Conversion Line"],
    color="blue",
    label="Conversion Line (텐칸센)",
    linewidth=2,
)
ax2.plot(
    ichimoku_data_msft.index,
    ichimoku_data_msft["Base Line"],
    color="red",
    label="Base Line (기준선)",
    linewidth=2,
)
ax2.fill_between(
    ichimoku_data_msft.index,
    ichimoku_data_msft["Leading Span A"],
    ichimoku_data_msft["Leading Span B"],
    where=ichimoku_data_msft["Leading Span A"] >= ichimoku_data_msft["Leading Span B"],
    facecolor="green",
    alpha=0.2,
    label="상승 클라우드",
)
ax2.fill_between(
    ichimoku_data_msft.index,
    ichimoku_data_msft["Leading Span A"],
    ichimoku_data_msft["Leading Span B"],
    where=ichimoku_data_msft["Leading Span A"] < ichimoku_data_msft["Leading Span B"],
    facecolor="red",
    alpha=0.2,
    label="하락 클라우드",
)

# AMD에 대한 범례 및 레이블 사용자 정의
ax2.legend(loc="upper left")
ax2.set_xlabel("날짜", fontsize=14)
ax2.set_ylabel("가격", fontsize=14)
ax2.set_title("이치모쿠 클라우드 차트 (AMD)", fontsize=16)
ax2.grid(True, linestyle="--", alpha=0.5)
ax2.set_facecolor("#f7f7f7")
ax2.tick_params(axis="both", which="major", labelsize=12)

# 서브플롯 간의 간격 조정
plt.tight_layout()

# 플롯 보기
plt.show()

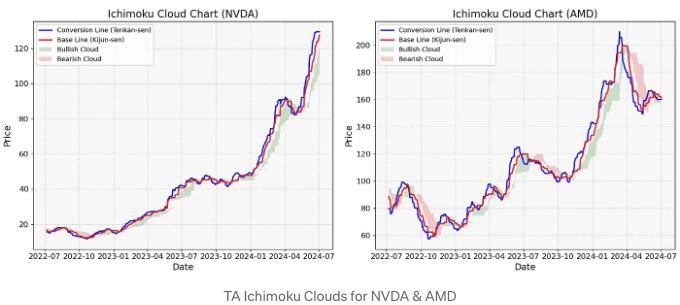
• 이 그래프는 NVDA 및 AMD가 각각 상승 및 하락하는 단기 추세를 따르는 것을 보여줍니다. AMD 플롯을 보면 2024년 7월에 Tenkan Sen(파란색 선)과 Kijun Sen(빨간색 선)이 명확히 교차하는 것을 볼 수 있습니다.

1년 빅테크 주가 예측

• FinanceToolkit이 1년 빅테크 주식을 예측할 수 있나요?
• 회사 티커로 Toolkit을 초기화하고 1년 주식 가격 시뮬레이션을 플로팅하기 [9]

# 회사 티커로 Toolkit을 초기화합니다
회사 = Toolkit(
    ["AAPL", "MSFT", "GOOGL", "AMZN"], api_key=API_KEY, start_date="2005-01-01"
)

주가모의실험 = 회사.options.get_stock_price_simulation(timesteps=10)

fig, ax = plt.subplots(2, 2, figsize=(15, 10))

주가모의실험_전치 = 주가모의실험.T
주가모의실험_전치.index = (
    주가모의실험_전치.index.astype("datetime64[ns]")
)

for i, 티커 in enumerate(회사._tickers):
    ax[i // 2, i % 2].plot(주가모의실험_전치[티커])
    ax[i // 2, i % 2].set_title(티커)
    ax[i // 2, i % 2].xaxis.set_tick_params(rotation=20)
    ax[i // 2, i % 2].yaxis.set_tick_params(labelsize=8)
    ax[i // 2, i % 2].grid(linestyle="--", alpha=0.5)

fig.suptitle("주가 모의실험", fontweight="bold")
fig.tight_layout()
plt.show()

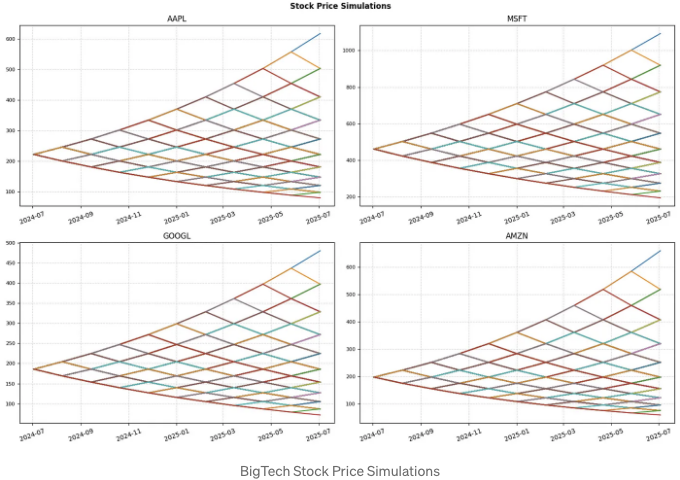
• 이러한 예측은 시간이 흐름에 따른 자본 가격의 이항 리턴 분포에 기반합니다. 이 모델에서는 각 반복마다 두 가지 가능한 결과가 있습니다 — 상승하거나 하락하며, 이는 이항 트리를 따릅니다.
• 시간에 따라 이 두 값을 그리는 것은 이항 트리를 만드는 것으로 알려져 있습니다. 이항 모델에 대한 자세한 내용은 Equity Derivatives의 가격 결정 및 분석(금융 Toolbox)을 참조하십시오.
• 이 모델은 직관적이며 잘 알려진 Black-Scholes 모델보다 실무에서 더 자주 사용됩니다.

META 캔들스틱 & 기술 분석 지표

• 마침내, 지난 729일 동안의 META TA 전략들을 탐색해 보겠습니다.
• 주식 데이터 읽기

ticker="META"
dfme = yf.download(ticker, start = '2020-01-01')

• META 캔들스틱 차트 2020–2024 및 TA 지표 표시

# 이동평균 추가
dfme['EMA9'] = dfme['Adj Close'].ewm(span = 9, adjust = False).mean() # 지수 이동평균 9기간
dfme['SMA20'] = dfme['Adj Close'].rolling(window=20).mean() # 단순 이동평균 20기간
dfme['SMA50'] = dfme['Adj Close'].rolling(window=50).mean() # 단순 이동평균 50기간
dfme['SMA100'] = dfme['Adj Close'].rolling(window=100).mean() # 단순 이동평균 100기간
dfme['SMA200'] = dfme['Adj Close'].rolling(window=200).mean() # 단순 이동평균 200기간

# 14기간 RSI 추가
delta = dfme['Adj Close'].diff() # 델타 계산
gain = delta.where(delta > 0,0) # 상승값 획득
loss = -delta.where(delta < 0,0) # 하락값 획득
avg_gain = gain.rolling(window=14).mean() # 14기간 평균 상승값 측정
avg_loss = loss.rolling(window=14).mean() # 14기간 평균 하락값 측정
rs = avg_gain/avg_loss # RS 계산
dfme['RSI'] = 100 - (100 / (1 + rs)) # 데이터 프레임에 RSI 열 생성

# 20기간 볼린저 밴드 추가
dfme['BB_UPPER'] = dfme['SMA20'] + 2*dfme['Adj Close'].rolling(window=20).std() # 상단 밴드
dfme['BB_LOWER'] = dfme['SMA20'] - 2*dfme['Adj Close'].rolling(window=20).std() # 하단 밴드

# 14기간 ATR 추가
dfme['TR'] = pd.DataFrame(np.maximum(np.maximum(dfme['High'] - dfme['Low'], abs(dfme['High'] - dfme['Adj Close'].shift())), abs(dfme['Low'] - dfme['Adj Close'].shift())), index = dfme.index)
dfme['ATR'] = dfme['TR'].rolling(window = 14).mean() # 데이터 프레임에 ATR 열 생성

# 지표와 함께 캔들스틱 차트 표시
fig = make_subplots(rows=4, cols=1, shared_xaxes=True, vertical_spacing=0.05,row_heights=[0.6, 0.10, 0.10, 0.20])

# 캔들스틱
fig.add_trace(go.Candlestick(x=dfme.index,
                             open=dfme['Open'],
                             high=dfme['High'],
                             low=dfme['Low'],
                             close=dfme['Adj Close'],
                             name='META'),
              row=1, col=1)

# 이동평균
fig.add_trace(go.Scatter(x=dfme.index,
                         y=dfme['EMA9'],
                         mode='lines',
                         line=dict(color='#90EE90'),
                         name='EMA9'),
              row=1, col=1)

# 이하 생략
...

fig.show()

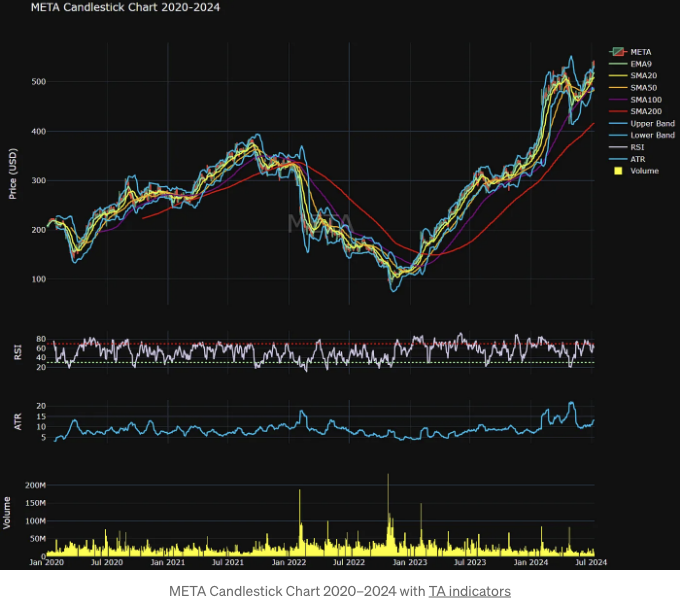
META RSI 대 MA 백테스팅

• 기술적 분석 백테스팅: 지난 729일 동안의 일별 META 데이터에서 RSI 및 MA 전략의 기대 수익 비교

end_date = dt.datetime.now() # 3월 21일 날짜를 정의
start_date = end_date - dt.timedelta(days=729) # 지난 729일 동안의 시간별 데이터 로딩

hourly_eur_usd = yf.download('META', start=start_date, end=end_date, interval='1d')
hourly_eur_usd 

           Open       High       Low        Close      Adj Close   Volume
Date      
2022-07-12 164.800003 165.910004 162.100006 163.270004 162.935181 16639700
2022-07-13 160.160004 164.979996 159.610001 163.490005 163.154739 16555100
2022-07-14 161.220001 162.589996 157.279999 158.050003 157.725891 23765200
2022-07-15 160.539993 164.979996 159.820007 164.699997 164.362244 23342800
2022-07-18 166.750000 171.690002 165.639999 167.229996 166.887054 23574300
... ... ... ... ... ... ...
2024-07-02 500.760010 510.500000 499.450012 509.500000 509.500000 7739500
2024-07-03 506.369995 511.279999 506.019989 509.959991 509.959991 6005600
2024-07-05 511.600006 540.869995 511.600006 539.909973 539.909973 21354100
2024-07-08 542.349976 542.809998 526.650024 529.320007 529.320007 14917500
2024-07-09 533.750000 537.479980 528.190002 530.000000 530.000000 8753200
501 rows × 6 columns

• RSI 백테스팅 전략 구현하기

# TA 라이브러리를 사용하여 RSI 계산하기
hourly_eur_usd['rsi'] = ta.momentum.RSIIndicator(hourly_eur_usd['Adj Close'], window=14).rsi()

# RSI 전략의 매개변수 정의
rsi_period = 14
overbought = 80
oversold = 40

# 신호를 저장할 새 열 생성
hourly_eur_usd['signal'] = 0 # 포지션을 가지지 않을 때 'signal' = 0

# 진입점 생성
for i in range(rsi_period, len(hourly_eur_usd)):
    if hourly_eur_usd['rsi'][i] > overbought and hourly_eur_usd['rsi'][i - 1] <= overbought:
        hourly_eur_usd['signal'][i] = -1 # 'signal' = -1 일 때 판매
    elif hourly_eur_usd['rsi'][i] < oversold and hourly_eur_usd['rsi'][i - 1] >= oversold:
        hourly_eur_usd['signal'][i] = 1 # 'signal' = 1 일 때 구매
        
# 통화쌍의 일일 수익률 계산
hourly_eur_usd['returns'] = hourly_eur_usd['Adj Close'].pct_change()
hourly_eur_usd['cumulative_returns'] = (1 + hourly_eur_usd['returns']).cumprod() - 1 # 기간의 총 수익률

# 신호를 수익에 적용
hourly_eur_usd['strategy_returns'] = hourly_eur_usd['signal'].shift(1) * hourly_eur_usd['returns']

# 전략의 누적 수익 계산
hourly_eur_usd['cumulative_strategy_returns'] = (1 + hourly_eur_usd['strategy_returns']).cumprod() - 1

# 초기 자본을 $100으로 설정
initial_capital = 100

# 전체 포트폴리오 가치 계산
hourly_eur_usd['portfolio_value'] = (1 + hourly_eur_usd['strategy_returns']).cumprod() * initial_capital

# 거래 수, 초기 자본, 최종 자본 출력
num_trades = hourly_eur_usd['signal'].abs().sum()
final_capital = hourly_eur_usd['portfolio_value'].iloc[-1]
total_return = (final_capital - initial_capital) / initial_capital * 100

print('\n')
print(f"거래 수: {num_trades}")
print(f"초기 자본: ${initial_capital}")
print(f"최종 자본: ${final_capital:.2f}")
print(f"총 수익률: {total_return:.2f}%")
print('\n')

# 포트폴리오 총 가치 플로팅
fig = go.Figure()

fig.add_trace(go.Scatter(x=hourly_eur_usd.index,
                         y=hourly_eur_usd['portfolio_value'].round(2),
                         mode='lines',
                         line=dict(color='#00BFFF'),
                         name='포트폴리오 가치'))

fig.update_layout(title='예상 수익 RSI 전략 META 데이터',
                  xaxis_title='날짜',
                  yaxis_title='가치 ($)',
                  template='plotly_dark',
                  height=600)

fig.show()

거래 수: 11
초기 자본: $100
최종 자본: $107.97
총 수익률: 7.97%

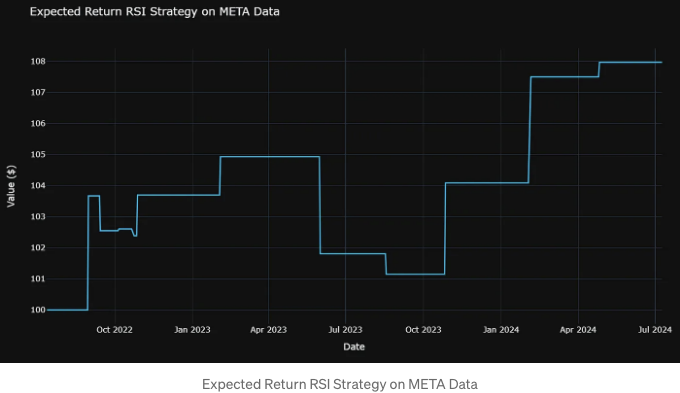
• MA 백테스팅 전략 구현하기

# TA 라이브러리를 사용하여 EMA 생성
ws = 5
wl = 10
hourly_eur_usd['ema9'] = ta.trend.ema_indicator(hourly_eur_usd['Adj Close'], window=ws)

# TA 라이브러리를 사용하여 SMA 생성
hourly_eur_usd['sma20'] = ta.trend.sma_indicator(hourly_eur_usd['Adj Close'], window=wl)

# 이동평균 교차 전략 매개변수 정의
short_ma = 'ema9'
long_ma = 'sma20'

# 신호를 저장할 새 열 생성
hourly_eur_usd['signal'] = 0

# 진입 신호 생성
for i in range(1, len(hourly_eur_usd)):
    if hourly_eur_usd[short_ma][i] > hourly_eur_usd[long_ma][i] and hourly_eur_usd[short_ma][i - 1] <= hourly_eur_usd[long_ma][i - 1]:
        hourly_eur_usd['signal'][i] = 1  # 매수 신호
    elif hourly_eur_usd[short_ma][i] < hourly_eur_usd[long_ma][i] and hourly_eur_usd[short_ma][i - 1] >= hourly_eur_usd[long_ma][i - 1]:
        hourly_eur_usd['signal'][i] = -1  # 매도 신호

# 총 수익률 계산
hourly_eur_usd['returns'] = hourly_eur_usd['Adj Close'].pct_change()
hourly_eur_usd['cumulative_returns'] = (1 + hourly_eur_usd['returns']).cumprod() - 1

# 수익률에 신호 적용
hourly_eur_usd['strategy_returns'] = hourly_eur_usd['signal'].shift(1) * hourly_eur_usd['returns']

# 누적 수익률 계산
hourly_eur_usd['cumulative_strategy_returns'] = (1 + hourly_eur_usd['strategy_returns']).cumprod() - 1

# 초기 자본 설정
initial_capital = 100

# 포트폴리오 가치 총액 계산
hourly_eur_usd['portfolio_value'] = (1 + hourly_eur_usd['strategy_returns']).cumprod() * initial_capital

# 거래 횟수, 초기 자본, 최종 자본 출력
num_trades = hourly_eur_usd['signal'].abs().sum()
final_capital = hourly_eur_usd['portfolio_value'].iloc[-1]
total_return = (final_capital - initial_capital) / initial_capital * 100

print('\n')
print(f"거래 횟수: {num_trades}")
print(f"초기 자본: ${initial_capital}")
print(f"최종 자본: ${final_capital:.2f}")
print(f"총 수익률: {total_return:.2f}%")
print('\n')

# 전략 가치 그래픽화
fig = go.Figure()

fig.add_trace(go.Scatter(x=hourly_eur_usd.index,
                         y=hourly_eur_usd['portfolio_value'].round(2),
                         mode='lines',
                         line=dict(color='#00BFFF'),
                         name='포트폴리오 가치'))

fig.update_layout(title='META 데이터에 기대되는 결과 이동평균 교차 전략',
                  xaxis_title='날짜',
                  yaxis_title='가치 ($)',
                  template='plotly_dark',
                  height=600)

fig.show()

거래 횟수: 50
초기 자본: $100
최종 자본: $108.00
총 수익률: 8.00%

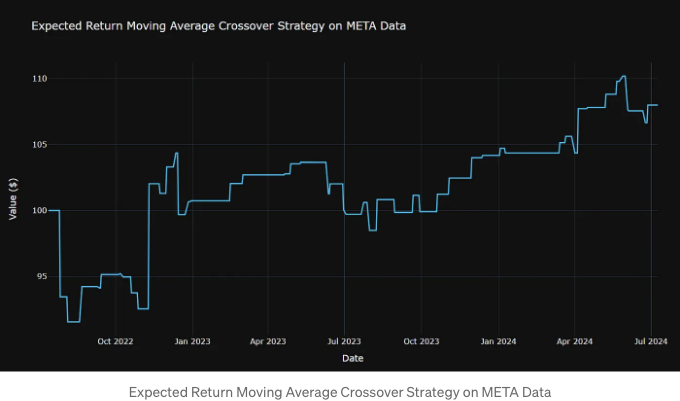
• RSI 및 MA 전략은 모두 2022년부터 2024년까지 META 데이터에서 약 8%의 예상 수익을 산출함을 확인할 수 있습니다. 그러나 거래 횟수 측면에서 RSI 전략이 더 우수함을 알 수 있습니다. 즉, 11 (RSI) vs 50 (MA).

결론

• 저희 사회의 디지털화가 급속히 증가함에 따라 미국 대형 기술 기업(Big Tech)들이 디지털 인프라와 플랫폼 소유를 통해 엄청난 부를 축적하고 영향력을 행사하게 되었습니다.
• 본 게시물에서는 기술적, 기본적 분석 도구와 최신 포트폴리오 최적화(PO) 알고리즘을 Python을 활용해 통합한 미국 Big Tech들의 양적 거래 분석을 제시했습니다.
• 우리는 기술적 분석 지표, 주식 기초 및 리스크 및 수익을 동시에 고려한 PO를 통합했습니다.
• 우리는 이번 연구 동안 Quantstats, TA, PyPortfolioOpt, Plotly, FinanceToolkit 라이브러리를 사용했습니다.
• 누적 수익, 첨도, 비대칭도, 상관 관계, 표준편차, 베타, 샤프 비율 등의 금융 지표를 분석했습니다.
• 2020년부터 2024년까지의 금융 성과인 등가 가중 포트폴리오와 최대 샤프 비율 포트폴리오와 S&P 전략을 비교했습니다(Sortino, Sharpe, Calmar, Treynor 비율, 켈리 기준, MTD, 최대 하락 폭, 베타, 알파, 연평균 복리 증가율 등).
• 2019년부터 2024년까지 NVDA 대 AMD 손익 계산서와 수익성 비율을 분석했습니다. 그리스 감능성, Value-at-Risk(VaR) 대 대조군, Fama-French 5 요인과의 상관 관계를 시각화했습니다.
• 주식 가격 예측에 대한 1년치 Big Tech 주가 예측을 시간별로 이루어진 자산 가격의 이항 분포를 따르는 움직임 상승 또는 하락 두 가지 결과를 지닌 이진 트리를 따라 반복하여 모델을 사용했습니다.
• 기술 시장의 감성 및 가격 모멘텀을 파악하기 위해 TA Ichimoku 클라우드를 활용했습니다.
• 마지막 729일의 META TA 전략을 탐색하면서 RSI 대 MA 크로스오버 거래 신호(백테스팅)의 예상 수익을 비교했습니다.
• TA 지표와 함께 2020년부터 2024년까지의 META 캔들스틱 차트는 주식 데이터 시각화에서 Plotly의 강력함을 보여 주었습니다.

참고 문헌

• Markowitz, H., 1952, PORTFOLIO SELECTION. The Journal of Finance.
• Markowitz meets technical analysis: Building optimal portfolios by exploiting information in trend-following signals
• Mastering Market Movements: Integrating Technical and Fundamental Analysis in Trading
• Fundamental vs. Technical Analysis: An Overview
• The Advantages and Disadvantages of Technical Analysis
• The pros and cons of fundamental analysis
• Fundamental Analysis: Advantages And Disadvantages
• Portfolio Optimization: How to Find Your Investment Balance
• Financial Analysis with the Finance Toolkit in Python

더 알아보기

• 주식 포트폴리오 위험/수익률 최적화
• 비트코인, 금, 원유 가격의 종합 분석
• Max(수익률/위험) 거래를 향하여
• 75가지 간단한 FinTA 지표를 사용한 NVDA 기술 분석

연락처

• 웹사이트
• GitHub
• X/Twitter
• Pinterest
• Mastodon
• Tumblr

면책사항

• 다음의 면책 조항은이 기사에 제공 된 정보가 교육 용도로만 사용되며 재정 건전성 또는 투자 자문으로 간주되어서는 안 된다는 것을 명확히합니다.
• 제공된 정보는 귀하의 개별 재정 상황, 목표 또는 리스크 허용도를 고려하지 않습니다.
• 귀하가 하는 어떠한 투자 결정이나 조치도 귀하의 전적인 책임입니다.
• 귀하의 재정 목표, 리스크 허용도 및 투자 시간표에 근거하여 어떤 투자의 적합성을 독립적으로 평가해야합니다.
• 귀하는 귀하의 특정 요구에 맞게 맞춤 지도를 제공할 수있는 인증 된 재무 전문가의 조언을 구하는 것이 좋습니다.
• 제공되는 도구, 데이터, 콘텐츠 및 정보는 개인의 투자 요구를 충족시키기 위해 맞춤화되지 않았습니다. 따라서 도구, 데이터, 콘텐츠 및 정보는 정보 및 교육 목적으로만 제공됩니다.