
양-장 변동성 추정자는 초고값 점프나 밤사이 갭을 가진 자산에 특히 유용한 역사적 변동성 측정값입니다. 이 추정자는 이전 게시된 로젤스-사첼과 가만-클라스 추정자의 장점을 결합해 단순한 변동성 측정값에서 발생하는 편향과 오류를 줄이도록 설계되었습니다.
이 기사에서는 이 변동성 측정치를 자세히 소개하고, 파이썬을 사용하여 시계열에 대한 롤링 계산 코드를 어떻게 작성하는지 보여줍니다.
양-장 변동성 이해하기
복잡한 변동성 모델에 대해 논의하기 전에, 항상 가장 기본적인 변동성 모델(또는 계산) 즉, 역사적 표준 편차에 대해 잘 이해하는 것이 좋습니다. 역사적 방법을 사용한 표준 편차는 금융 상품의 변동성을 측정하는 일반적인 방법으로, 과거 가격 데이터를 기반으로 합니다.
이는 일련의 값들의 변동이나 분산량을 정량화합니다. 금융에서는 일반적으로 일일 수익률이 그들의 평균 주변에서 얼마나 퍼져있는지를 측정합니다. 표준 편차를 계산하는 단계는 다음과 같습니다:
- 차분(첫 번째 함수) 또는 로그 방법(두 번째 함수)을 사용하여 수익률을 계산합니다.
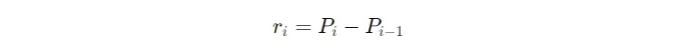
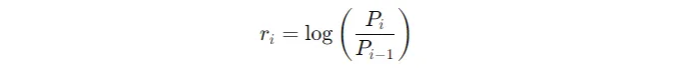
- 수익률의 평균(평균)을 계산하세요:
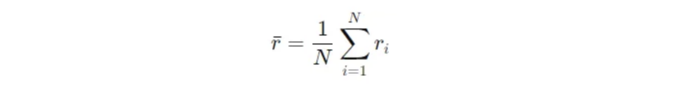
- 일일 수익률의 분산을 계산하세요:
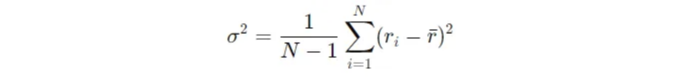
- 표준 편차는 분산의 제곱근이다:
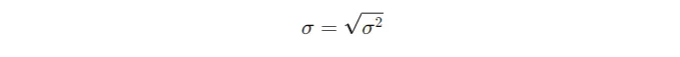
어떤 통계적 측정 값처럼 장단점이 있습니다. 역사적 표준 편차는 쉽게 계산할 수 있습니다. 스프레드시트 및 프로그래밍 언어에서 쉽게 구현할 수 있는 기본 통계 작업이 필요합니다. 변동성에 대한 공식적인 측정 방법으로 이해되며, 깊은 통계 배경을 갖지 않을 수 있는 이해관계자들에게 쉽게 설명할 수 있습니다. 많은 금융 모델 및 위험 지표(예: 샤프 비율)는 리스크 측정 값으로서 표준 편차를 의존합니다.
샘플 크기가 작은 경우, 역사적 표준 편차는 실제 변동성을 과소평가하는 경향이 있습니다. 이 편향은 자산의 리스크에 대한 잘못된 결론으로 이어질 수 있습니다. 이 방법은 분석 기간 동안 자산의 기저 변동성이 일정하다고 가정합니다. 실제로 변동성은 시간이 지남에 따라 변할 수 있으므로 이 가정은 현실적이지 않습니다.
게다가, 금융 수익은 종종 꼬리가 두꺼운 경향(leptokurtosis)과 비뚤림을 나타내며, 이는 정규 분포를 따르지 않음을 의미합니다. 표준 편차는 이러한 특성을 포착하지 못하며, 결과적으로 리스크를 과소평가할 수 있습니다.
Nvidia의 일일 수익에 대한 롤링 5일 변동성 측정치를 계산하기 위해 Python에서 다음 코드를 사용해보세요:
import numpy as np
import matplotlib.pyplot as plt
import yfinance as yf
def calculate_rolling_historical_volatility(data, window):
# 수익률 계산 (차분 방법 사용)
returns = data['Close'] - data['Close'].shift(1).dropna()
# 수익률의 롤링 표준 편차 계산
rolling_volatility = returns.rolling(window=window).std()
# 표준 편차 측정 값을 포함하는 변수 반환
return rolling_volatility
# Nvidia의 역사적 값 다운로드
df = yf.download("NVDA", start="2022-01-01", end="2024-06-30")
# 롤링 윈도우 크기 정의
window_size = 5
# 공식 적용 및 변동성 데이터프레임 얻기
rolling_volatility = calculate_rolling_historical_volatility(df, window=window_size)
# 시간에 따른 변동성 플로팅
plt.plot(rolling_volatility, color='black', label='5일 주기 역사적 표준 편차')
plt.legend()
plt.grid()
plt.axhline(y=np.mean(rolling_volatility), color='red', linestyle='dashed')
Yang-Zhang 변동성 추정기는 Rogers-Satchell 및 Garman-Klass 추정기의 장점을 결합한 과거 변동성 측정치이다. 이는 특히 고개를 넘는 높은 가격 변동이나 야간 갭이 있는 자산에 유용하다. 이 추정기는 더 간단한 변동성 추정기에 존재하는 편향 및 오차를 줄이도록 설계되었다.
Yang-Zhang 변동성 추정기는 다음 공식을 사용하여 계산된다:
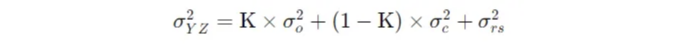
참고:
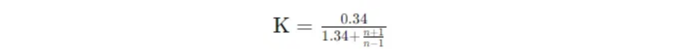
첫 번째 표준 편차 용어는 open-close 변동성을 나타내고, 두 번째는 close-close 변동성을 나타내며, 세 번째는 Rogers-Satchell 변동성 추정값입니다.
K factor는 open-close 변동성과 close-close 변동성의 기여도를 균형 있게 조정하며, 표본 크기 n에 대한 보정을 합니다. 양-장(Estimators) 추정자는 다른 추정자들과 비교하여 개시 가격의 급등과 종가 변동에 덜 민감하며, 상당한 야간 갭을 경험하는 자산에 대해 더 견고합니다.
더 많은 작업을 보려면, 그림에 첨부된 링크를 따라 가면 PDF 책 카탈로그를 찾을 수 있는 제 웹사이트를 방문해주세요!

Python에서 Yang-Zhang 변동성 계산하기
이제 Python을 사용하여 Yang-Zhang 변동성을 계산해 보겠습니다. 같은 예시를 사용할 것입니다 (즉, lookback 기간이 5인 Nvidia의 일일 수익률):
import numpy as np
import matplotlib.pyplot as plt
import yfinance as yf
import math
def yang_zhang(price_data, window_size=30, periods=252, clean=True):
log_ho = (price_data["High"] / price_data["Open"]).apply(np.log)
log_lo = (price_data["Low"] / price_data["Open"]).apply(np.log)
log_co = (price_data["Close"] / price_data["Open"]).apply(np.log)
log_oc = (price_data["Open"] / price_data["Close"].shift(1)).apply(np.log)
log_oc_sq = log_oc ** 2
log_cc = (price_data["Close"] / price_data["Close"].shift(1)).apply(np.log)
log_cc_sq = log_cc ** 2
rs = log_ho * (log_ho - log_co) + log_lo * (log_lo - log_co)
close_vol = log_cc_sq.rolling(window=window_size, center=False).sum() * (
1.0 / (window_size - 1.0)
)
open_vol = log_oc_sq.rolling(window=window_size, center=False).sum() * (
1.0 / (window_size - 1.0)
)
window_rs = rs.rolling(window=window_size, center=False).sum() * (1.0 / (window_size - 1.0))
k = 0.34 / (1.34 + (window_size + 1) / (window_size - 1))
result = (open_vol + k * close_vol + (1 - k) * window_rs).apply(
np.sqrt
) * math.sqrt(periods)
if clean:
return result.dropna()
else:
return result
# Nvidia의 과거 값 다운로드
df = yf.download("NVDA", start="2020-01-01", end="2024-06-30")
# Rolling window 크기 정의
window_size = 5
# 식 적용 및 변동성 데이터 프레임 가져오기
rolling_volatility = yang_zhang(df)
# 시간대별 변동성 플롯
plt.plot(rolling_volatility, color='black', label='5-period Yang-Zhang 변동성')
plt.legend()
plt.grid()
plt.axhline(y=np.mean(rolling_volatility), color='red', linestyle='dashed)

과거 표준 편차는 변동성의 유용하고 널리 채택된 측정 방법이며, 간단함, 계산의 용이성 및 금융 산업에서의 일반적인 수용으로 인해 가치가 있습니다. 그러나 작은 표본 크기, 비정상적 변동성 및 수익의 비정규 분포를 처리하는 데 있어서 특히 한계가 있어 조심해서 사용해야 합니다.
정확성이 중요하거나 표본 크기가 작은 경우, 대안적인 변동성 모델이 더 나은 리스크 평가를 제공할 수 있습니다.