이사는 어려워요. 솔직히 말해서, 매우 귀찮아요. 좀 짜증나죠. 특히 새로 이사갈 곳이 없으면 더 어려워요. 그런 경우에는 친구 집에 머물면서 물건을 임시 보관할 곳을 빌려야 할 수도 있는데, 보관 장소는 사용 면적에 따라 요금을 부과하기 때문에 가격이 비싸질 수 있어요. (그런 일은 절대 없다고 하시기 전에, 프랑스에서 폴란드로 이사 올 때 제 친구 중 한 명에게 일어났던 정황을 알려드립니다.)

개인에게 이사가 이미 어려운 상황이라면, 정식으로 이사를 하고 전체 공장을 임시 보관하는 작업의 복잡함을 상상해보세요. 아마 "와, 루이스, 이건 미친 소리인데"라고 생각하실 수도 있지만, 실제로 이런 상황이 발생해요. 제게도 일어난 일이었고, 그 당시에는 이를 처리할 수 있는 분석 도구가 없었어요.

저는 석유 및 가스 서비스 업종에서 일했었어요. 나라 내에서 비즈니스 환경이 급격히 악화되고 불안정해졌던 시기가 있었어요. 일부 서비스에 대해서는 상황이 더 이상 지속할 수 없어져, 경영진이 손실을 줄이기 위해 그 서비스를 폐쇄하기로 결정했어요. 이 서비스들이 발생한 중요한 비용 중 하나는 운영 시설의 임대료인데, 임대료를 절약하기 위해 그 시설을 사용 중지하는 것이 합리적이었어요. 그러나 시설을 폐쇄한다는 것은 전체 작업장을 닫고 모든 자산을 보관 장소로 이동해야 한다는 것을 의미했어요. 기억하세요, 이건 석유 및 가스 산업입니다. 이 자산들은 수십억 달러의 가치를 지닌 고도로 정교한 도구들이에요. 이 자산 중 일부 스페어 파츠만 수천 달러의 가치를 지니며 도둑질과 불법 시장 매매의 쉬운 표적이었어요. 그래서 도전 과제는 자산을 이동시키는 것뿐만 아니라 임시로 보관하고 그 중요성을 지키는 것이었어요.

제 매니저인 뛰어난 분이 이 문제를 제게 제기했어요. 우리는 전체 서비스 부문의 모든 자산을 본 시설로 이전하여 안전하고 제한된 공간에 보관할 계획이라고 말씀해 주셨어요. 이러한 자산들이 매우 귀중하기 때문에 도난이나 손상 가능성을 최대한 피하고 싶었습니다. 특히 몇몇 특수 트럭은 수천 달러가치의 부품이 장착되어 있었고, 국가의 상황을 감안할 때 도난 유혹이 높았어요. 따라서, 관리 부서의 허락이 없는 한 누구도 안전 구역에 들어가선 안 되었죠. 이 규칙을 시행하기 위해 우리는 전기 울타리와 경계를 침범한 사람이 있을 경우 알람이 울리도록 연결된 적외선 센서로 해당 영역을 둘러쌌어요 (진짜 말이죠; 이건 실화입니다). 그러나 이 계획의 문제는 그 모든 방어 조치가 비용이 많이 든다는 것이었고, 이 방어 시스템을 빌려주는 회사는 총 둘러싸인 영역을 기준으로 비용을 부과했어요. 제 매니저는 안전 구역 면적을 최소화하여 비용을 줄이기 위해 이 자산들의 공간 배치 방법을 찾아보라고 했어요. 전기 울타리 회사는 둘러싸인 영역이 직사각형이나 정사각형이어야 한다고 요구했어요. 게다가, 자산에 손상을 피하기 위해 자산을 쌓을 수 없었죠 (트럭 위에 다른 트럭을 올릴 수 없어요). 그래서 우리는 문서에 공통되게 "조합 문제"라고 알려진 이차원 저장 문제를 다루게 되었어요.

수학적 프로그래밍 능력으로 이 문제를 해결했다고 말씀 드리고 싶지만, 그렇지는 않아요. 이것은 나에게 박사 학위를 취득하기 훨씬 이전의 일이었고, 그 당시에는 이 문제를 수학적 최적화로 어떻게 다루어야 하는지 조차 모르고 있었거든요 - 사실, 어떻게 검색을 시작해야 하는지에 대해선 전혀 알고 있었을 리도 없었어요 (문제가 "조합 문제"라는 걸 어떻게 알고 시작해야 하는지 말이죠?). 삶에선 때로는 아무것도 모르는 걸 모르는 법이 있어요.

사실, 이러한 문제를 해결하는 방법을 배우는 것이 제 학습을 계속하는 주된 동기였어요. 그래서 이 기사에서는 이 문제를 어떻게 구성하는지, 파이썬과 gurobipy를 사용하여 어떻게 해결하는지, 그리고 마지막에는 이를 해결하기 위해 적용할 수 있는 일부 휴리스틱 절차에 대해 간단히 이야기할 거예요.

Gurobi를 사용해본 적이 없다면, 특히 Google Colab에서 사용하는 경우, Gurobi 웹 라이선스를 Colab 환경에 설정하는 방법을 설명한 이전의 제 글 중 하나를 읽어보시기를 권유드립니다. 아래에서 해당 글 링크를 찾아볼 수 있어요:

만약 선형 프로그래밍(LP) 또는 정수 프로그래밍(IP) 기술에 대한 자습서와 더 많은 정보가 필요하다면, Bruno가 쓴 훌륭한 글들을 확인하는 걸 강력 추천해요. 또 다른 좋은 소스는 William의 수학적 프로그래밍에 대한 책이에요 [1].

글 목차:

Assortment 문제
라이브러리 설치 및 Colab 환경 설정
입력 데이터 및 전처리
Gurobipy로 문제 해결
구성적 휴리스틱 솔루션
휴리스틱에서 웜 스타트를 통한 문제 해결
결론
참고 문헌

아이템 조합 문제

아이템 조합 문제의 일반적인 버전은 큰 세트에서 항목의 부분집합을 선택하여 선반 공간이나 예산과 같은 제약 조건 하에 수익 또는 이윤을 극대화하는 것을 포함합니다. 이는 소매 및 운영 관리에서 흔히 볼 수 있는 문제로, 최적화 기술과 종종 소비자 선택 모델링을 포함합니다. 이 글에서 다루는 특정 아이템 조합 문제는 물류 및 생산 상황에서 자주 나타나는 2D 직사각형 패킹 문제로도 알려져 있습니다.

이 문제에서의 목표는 개별 작은 단위가 잘릴 수 있는 객체의 최소 크기를 결정하는 것입니다. 형식적으로는, 동일하거나 다른 크기의 직사각형 모음을 최소 영역 내에 서로 겹치지 않도록 배치하는 문제로 정의될 수 있습니다. 시설 배치 상황에서 이 문제는 여러 응용이 있으며, 이를 해결하기 위한 다양한 휴리스틱 접근법이 있습니다.

이 문제에 필요한 변수는 다음과 같습니다:

변수 x_i와 y_i는 우리 문제의 각 "사각형" 자산의 (x, y) 좌표에 해당합니다. 모든 자산 또는 직사각형을 포함하는 I 집합이 있습니다.
변수 b_i_j_k는 모델에서 "OR" 조건을 설정하기 위해 필요한 보조 이진 변수이며, 사용 방법은 나중에 자세히 설명됩니다.
변수 X와 Y는 모든 자산을 배치하여 얻은 총 폭과 총 높이에 해당하며, 이 두 변수를 사용하여 모든 자산을 저장하는 데 사용된 총 면적을 계산할 것입니다.
마지막으로 각 직사각형 i는 회전할지 여부를 결정하는 변수 r_i를 갖게 됩니다.

다음과 같은 포맷을 사용하여 문제를 모델링할 수 있습니다

위의 공식은 처음에는 복잡해 보일 수 있지만 실제로는 꽤 간단합니다. 목적 함수는 총 면적에 해당하며, 이는 폭과 높이인 X와 Y의 곱입니다.

제약 조건 (1)은 총 폭 값 X가 각 항목의 x 좌표와 너비를 더한 것보다 커야 함을 보장합니다. 비슷하게, 제약 조건 (2)은 총 높이 값 Y가 각 항목의 y 좌표와 높이를 더한 것보다 커야 함을 보장합니다.

제약 조건 (3-7)은 서로 다른 항목들의 위치 간에 겹침이 없도록 보장합니다. 이러한 제약 조건은 각 항목에 대해 변수 b_i_j_1, b_i_j_2, b_i_j_3 및 b_i_j_4를 이용하며 Big-M 방법을 활용하여 OR 조건으로 작동합니다. 요약하면 한 항목은 다른 항목의 왼쪽, 오른쪽, 위 또는 아래에 위치할 수 있지만, 절대로 겹치지 않습니다.

제약 조건 (8-11)은 변수가 적절한 도메인에 속하는 것을 보장합니다.

라이브러리 설치 및 콜랩 환경 설정하기

구글 콜랩에서 Gurobi를 사용하려면 먼저 다음 코드를 사용하여 설치해야 합니다:

!pip install gurobipy

설치가 완료되면 이 프로젝트에 필요한 라이브러리를 가져올 수 있습니다.

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.patches import Rectangle
from itertools import chain, combinations, permutations, product
import gurobipy as gp
from gurobipy import GRB
from copy import deepcopy

또한 gurobi 세션을 초기화해야 하므로 gurobi 라이선스의 모든 관련 정보를 포함한 params 사전을 만들어야 합니다.

WLSACCESSID = '< 여기에 귀하의 WLSACCESSID를 복사하세요 >'
WLSSECRET = '< 여기에 귀하의 WLSSECRET를 복사하세요 >'
LICENSEID = '< 여기에 귀하의 LICENSEID를 복사하세요 >'

params = {
"WLSACCESSID": WLSACCESSID,
"WLSSECRET": WLSSECRET,
"LICENSEID": LICENSEID,
}
env = gp.Env(params=params) #이 줄은 gurobi 환경을 초기화합니다

입력 데이터 및 전처리

간편함을 위해, 7가지 다른 차원의 34개 아이템만 사용하겠습니다. 이 값들은 설명을 위해 작게 유지했습니다. 이전 경험상으로는 수백 개의 엄청난 크기의 자산들과 실제로 무거운 화물 트럭들도 처리해야 했었습니다. 예시 아이템들의 차원은 표 1에 나와 있습니다.

데이터를 사용할 수 있도록 보장하기 위해, 서로 다른 값을 리스트에 저장한 다음, 각 항목을 따로 행으로 준비한 확장된 데이터프레임을 만들 것입니다. 다음 코드로 이를 실현할 수 있습니다:

widths = [4,1,2,3,2,6,10]
heights = [3,1,1,2,4,2,4]
quants = [4,10,8,5,2,3,2]

WIDTHS = []
HEIGHTS = []
for q, w, h in zip(quants, widths, heights):
  for x in range(q):
    HEIGHTS.append(w)
    WIDTHS.append(h)

data_df = pd.DataFrame()
data_df['HEIGHTS'] = HEIGHTS
data_df['WIDTHS'] = WIDTHS

N = len(data_df) # 항목 개수
top = max(data_df['HEIGHTS'].sum(), data_df['WIDTHS'].sum()) # X 또는 Y의 최댓값
M = top # OR 조건에 사용될 큰 M

I = range(N) # 각 자산 "i"의 인덱스
K = range(4) # OR 변수 "b"의 인덱스

Gurobipy로 문제 해결

이제 필요한 모든 라이브러리와 입력 데이터가 준비되었으니, Figure 3에 설명된 수학 모델을 생성할 차례입니다. GurobiPy를 사용하여 이 모델을 구현하려면 아래의 코드 스니펫을 따르면 됩니다:

model = gp.Model("Assortment",env=env)

# (x,y) 좌표 변수
x = model.addVars(I,lb = 0,ub = top,vtype=GRB.CONTINUOUS, name="x")
y = model.addVars(I,lb = 0,ub = top,vtype=GRB.CONTINUOUS, name="y")

# 회전 변수
R = model.addVars(I,vtype=GRB.BINARY,name = 'R')

X = model.addVar(lb=0,ub = top,vtype = GRB.CONTINUOUS,name = "X")
Y = model.addVar(lb=0,ub = top,vtype = GRB.CONTINUOUS,name = "Y")

# OR 조건을 위한 b 변수
b_vars = [(i,j,k) for i in I for j in I if j!=i for k in K]
B = model.addVars(b_vars,vtype = GRB.BINARY,name = "B")

# 목적 함수
model.setObjective(X*Y,GRB.MINIMIZE);

# 제약 조건 (1) 및 (2)
for i in I:

  model.addConstr(X >= x[i] + WIDTHS[i]*R[i] + (1-R[i])*HEIGHTS[i])
  model.addConstr(Y >= y[i] + HEIGHTS[i]*R[i] + (1-R[i])*WIDTHS[i])


# 제약 조건 (3-7)
for i in I:
  for j in I:
    if i == j:
      continue
    else:
      #제약 조건 (3)
      model.addConstr(x[i] + WIDTHS[i]*R[i] + (1-R[i])*HEIGHTS[i] <= x[j] + M*(1-B[i,j,0]))
      #제약 조건 (4)
      model.addConstr(x[j] + WIDTHS[j]*R[j] + (1-R[j])*HEIGHTS[j] <= x[i] + M*(1-B[i,j,1]))
      #제약 조건 (5)
      model.addConstr(y[i] + HEIGHTS[i]*R[i] + (1-R[i])*WIDTHS[i] <= y[j] + M*(1-B[i,j,2]))
      #제약 조건 (6)
      model.addConstr(y[j] + HEIGHTS[j]*R[j] + (1-R[j])*WIDTHS[j] <= y[i] + M*(1-B[i,j,3]))
      #제약 조건 (7)
      model.addConstr(B[i,j,0] + B[i,j,1] + B[i,j,2] + B[i,j,3] >= 1)

참고로 제약 조건 (8–11)은 변수 생성 단계에서 설정되었으므로 model.addConstr 메서드를 통해 명시적으로 추가할 필요가 없습니다. 이제 모델이 완성되었으니 해결할 수 있습니다. 이 문제를 해결하기 위해 아래 코드를 따라주세요:

tl = 600
mip_gap = 0.05

model.setParam('TimeLimit', tl)
model.setParam('MIPGap', mip_gap)
model.optimize()

600초 후에도 최적 솔루션에는 아직 멀리 떨어져 있지만 사용 영역이 크게 줄어들었습니다. 초기 값 620에서 최종 값 238로 줄었습니다. 이는 초기 솔루션의 약 1/3에 해당하는 값입니다. 나쁘지 않죠.

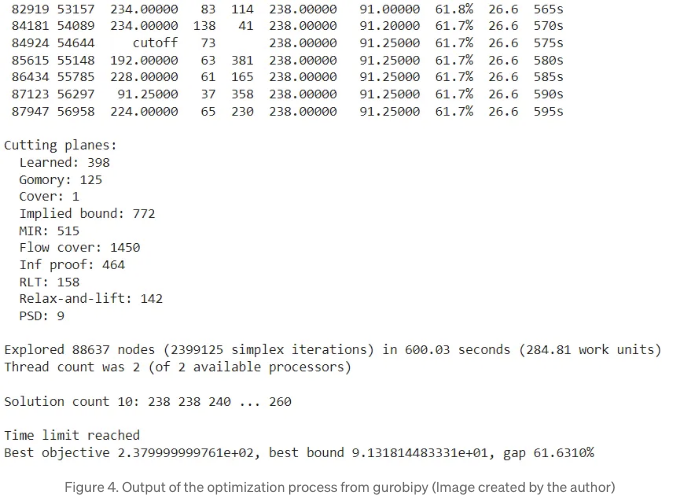
문제가 해결되었으므로 솔루션을 추출하고 플롯해야 합니다. 다음 코드를 따라하기만 하면 matplotlib의 Rectangle 객체를 사용하여 쉽게 이 작업을 수행할 수 있습니다:

all_vars = model.getVars()
values = model.getAttr("X", all_vars)
names = model.getAttr("VarName", all_vars)

obj = round(model.getObjective().getValue(),0)

total_X = int(round((X.x),0))
total_Y = int(round((Y.x),0))

fig, ax = plt.subplots()

for item in I:

  coords = (x[item].x,y[item].x)

  if R[item].x <= 0.01:
    wid = HEIGHTS[item]
    hig = WIDTHS[item]
  else:
    wid = WIDTHS[item]
    hig = HEIGHTS[item]

  ax.add_patch(Rectangle(coords, wid, hig,
            edgecolor = 'black',
            facecolor = "Grey",
            fill = True,
            alpha = 0.5,
            lw=2))
ax. set_xlim(0, total_X )
ax. set_ylim(0, total_Y )

ax.set_xticks(range(total_X+1))
ax.set_yticks(range(total_Y+1))
ax.grid()
ax.set_title(f" Total area {total_X} x {total_Y} = {int(obj)}")

plt.show()

아래의 그림 5에서 얻은 조합 솔루션을 시각화할 수 있습니다.

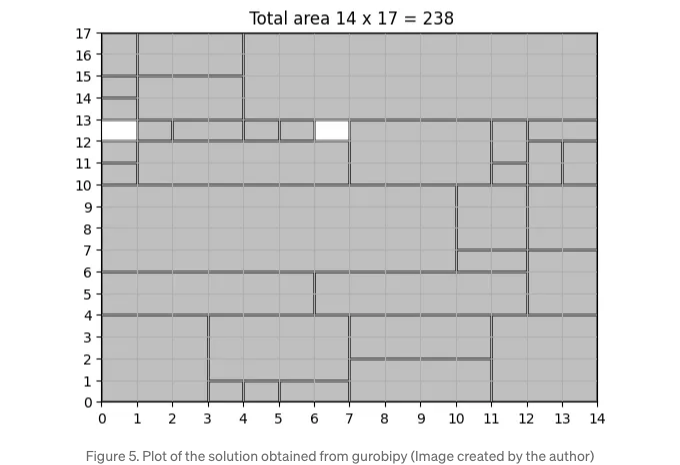
마지막으로, 솔루션을 데이터프레임에 저장할 수 있습니다. 이후 동료와 공유하고 싶을 때 CSV 또는 Excel 파일로 다운로드할 수 있습니다. 아래 코드 스니펫을 따라하면 됩니다:

output_list = []
for i in I:
  print(f"item {i} x:{x[i].x}, y:{y[i].x}, Rotated:{R[i].x <= 0.01}")
  row = {'item':i,'x':round(x[i].x,2),'y':round(y[i].x,2),'Rotated':R[i].x <= 0.01}
  output_list.append(row)

output_df = pd.DataFrame(output_list)
output_df.to_csv("output_solution.csv") # 솔루션을 .csv 파일로 다운로드

휴리스틱 솔루션 구성

소개에서 언급한대로, 이 문제를 이전 섹션의 수학적 프로그래밍 공식을 사용하여 최적으로 해결하고 싶었지만, 이 도전에 처음 직면할 때 이러한 기술을 알지 못했습니다. 그러나 그렇다고 해서 해결책을 제공하지 않았던 것은 아닙니다. 사실, 모든 자산을 정리하고 안전한 영역에 포장했습니다. 솔루션은 최적은 아니지만, 그래도 솔루션이었습니다. 어떻게 하였을까요? 아마도 휴리스틱이나 여러 가지 휴리스틱의 조합을 사용했을 것입니다.

정식으로는, 휴리스틱이란 "완전히 최적화되거나 완전히 최적화되지 않은, 완벽하게 되찾거나 합리화되지 않은 현실적인 방법을 사용하는 문제 해결 방법"입니다. 우리는 인지하지 못해도, 우리는 상당히 휴리스틱을 적용하여 문제를 해결하며, 이 문제 조합 문제도 예외가 아닙니다. 다양한 구성 휴리스틱을 만들어낼 수 있습니다. 다음 섹션에서 두 가지에 대해 논의할 것입니다.

FFDH: 첫 번째 적합 감소 높이 휴리스틱

이 접근 방식으로는, 간단히 사각형을 높이 순으로 정렬한 다음 각 자산을 왼쪽에서 오른쪽으로 이동하면서 맞는 첫 번째 위치에 배치합니다. 이 휴리스틱을 구현하기 위해 Python에서 새로운 클래스를 만든 후 해당 클래스의 인스턴스와 함께 작동하는 함수로 휴리스틱을 개발할 것입니다. 아래의 코드를 사용하여 간단히 새 클래스를 만들고 각 자산을 인스턴스화할 수 있습니다:

# 새 클래스 정의
class Rectangle_class:
    # 생성자
    def __init__(self, width, height, index):
        self.width = width
        self.height = height
        self.x = 0
        self.y = 0
        self.index = index

# 모든 자산의 목록 만들기
rectangles = [] 

# 각 자산을 위해 사각형 인스턴스 초기화
for i in range(len(data_df)): 
    h, w = data_df.iloc[i,0], data_df.iloc[i,1]
    REC = Rectangle_class(w, h, i)
    rectangles.append(REC)

아래의 코드를 사용하여 휴리스틱 함수를 구현할 수 있습니다:

def ffdh(rectangles):
    # 높이를 기준으로 사각형 정렬(내림차순)
    rectangles.sort(key=lambda rect: rect.height, reverse=True)

    # 위치 추적을 위한 변수 초기화
    current_y = 0
    current_x = 0
    row_height = 0
    total_width = 0

    for rect in rectangles:
        if current_x + rect.width > total_width:
            total_width = current_x + rect.width
        # 현재 행에 사각형이 맞는지 확인
        if current_x + rect.width <= total_width:
            rect.x = current_x
            rect.y = current_y
            current_x += rect.width
            row_height = max(row_height, rect.height)
        else:
            # 다음 행으로 이동
            current_y += row_height
            rect.x = 0
            rect.y = current_y
            current_x = rect.width
            row_height = rect.height

    total_height = current_y + row_height
    return rectangles, total_width, total_height

이 함수는 수정된 좌표와 함께 자산의 총 너비와 높이를 반환합니다. 이 휴리스틱을 사용하여 34개의 자산 문제에 대해 어떤 결과를 얻을 수 있는지 확인해보겠습니다.

# 함수 호출 및 출력값 저장
packed_rectangles, total_width, total_height = ffdh(rectangles)

total_X = total_width
total_Y = total_height

# 사용된 최종 영역 계산
obj = total_X * total_Y

# 솔루션 플롯
fig, ax = plt.subplots(figsize=(16, 6))

for rect in packed_rectangles:
    coords = (rect.x, rect.y)
    wid, hig = rect.width, rect.height

    ax.add_patch(Rectangle(coords, wid, hig,
            edgecolor='black',
            facecolor="Grey",
            fill=True,
            alpha=0.5,
            lw=2))
ax.set_xlim(0, total_X)
ax.set_ylim(0, total_Y)

ax.set_xticks(range(total_X+1))
ax.set_yticks(range(total_Y+1))
ax.grid()
ax.set_title(f" 총 면적 {total_X} x {total_Y} = {int(obj)}")
plt.xticks(rotation=30)
plt.show()

얻은 출력 솔루션은 아래 그림 6에 표시되어 있습니다:

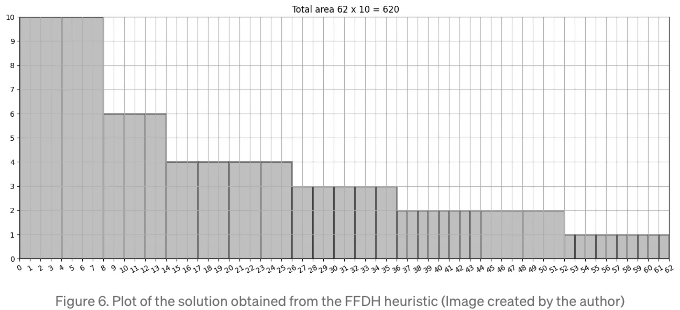
이 휴리스틱으로 제공된 솔루션은 총 620의 면적을 갖고 있습니다. 우연히도 이 값은 Gurobi의 시작점이기도 했습니다. 솔루버가 가지-및-한정 알고리즘을 시작하기 전에, 초기 솔루션을 미세 조정하기 위해 여러 휴리스틱을 적용하며, 아마도 이 휴리스틱이 하나일 것입니다.

선반 휴리스틱

이 휴리스틱은 최대 너비 제약 조건(우리가 제공하는 경우)으로 자산들을 높이 기준으로 정렬하여 평면 상에 배치합니다. 휴리스틱은 현재 선반이 가로 제한에 도달할 때까지 자산들을 배치하고, 그 후에 새로운 선반으로 이동하여 총 너비와 높이를 갱신합니다. 아래 함수를 사용하여 휴리스틱을 구현했습니다:

def shelf_heuristic(rectangles, max_width):
    # 자산들을 높이 기준으로 내림차순 정렬
    rectangles.sort(key=lambda rect: rect.height, reverse=True)

    current_x = 0
    current_y = 0
    shelf_height = 0

    for rect in rectangles:
        if current_x + rect.width > max_width:
            # 새로운 선반으로 이동
            current_x = 0
            current_y += shelf_height
            shelf_height = 0

        # 직사각형 배치
        rect.x = current_x
        rect.y = current_y
        current_x += rect.width
        shelf_height = max(shelf_height, rect.height)

    total_width = max([rec.x + rec.width for rec in rectangles])
    total_height = max([rec.y + rec.height for rec in rectangles])

    return rectangles, total_width, total_height

좌표와 폭, 높이 값을 결정한 뒤, 해당 사각형을 도형으로 그려보세요. 이것이 우리가 34개의 자산과 선반 너비 20을 사용했을 때 발생한 결과입니다. 결과는 아래 그림 7에 표시되어 있습니다:

container_width = 20
packed_rectangles,total_width, total_height = shelf_heuristic(rectangles, container_width)

total_X = total_width
total_Y = total_height

obj = total_X*total_Y

# 솔루션의 그래프 생성
fig, ax = plt.subplots(figsize=(16, 6))

for rect in packed_rectangles:

  coords = (rect.x,rect.y)
  wid,hig = rect.width,rect.height

  ax.add_patch(Rectangle(coords, wid, hig,
            edgecolor = 'black',
            facecolor = "Grey",
            fill = True,
            alpha = 0.5,
            lw=2))
ax. set_xlim(0, total_X )
ax. set_ylim(0, total_Y )

ax.set_xticks(range(total_X+1))
ax.set_yticks(range(total_Y+1))
ax.grid()
ax.set_title(f" Total area {total_X} x {total_Y} = {int(obj)}")
plt.xticks(rotation=30)
plt.show()

위 코드를 사용하여 얻은 출력 결과는 아래 그림 7에 표시되어 있습니다:

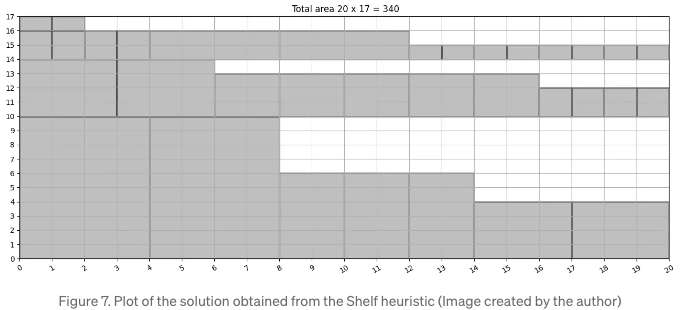
이 휴리스틱으로 제공된 솔루션은 총 340의 면적을 가지고 있으며, FFDH로부터 얻은 면적의 거의 절반이 됩니다. 이는 이 휴리스틱처럼 빠르게 실행되는 휴리스틱이며, 자산의 회전을 허용하지 않기 때문에 휴리스틱의 품질이 크게 향상될 것으로 예상되는 것을 고려할 때 훌륭합니다. 이 문제에는 수십 개의 휴리스틱이 있음을 유의해 주세요. 저희는 인기 있는 두 가지만 다루었을 뿐이니, 더 자세한 정보는 참고 문헌 [6-8]을 확인해 주세요.

아마도 "와, 루이스야, 이 340 면적에서 시작하는 솔버가 있으면 좋겠다"고 생각 중일 수도 있으시겠죠? 그렇다면 틀림없습니다. 그래서 다음 섹션에서 이에 대해 다룰 것입니다.

휴리스틱에서 시작하는 웜 스타트로 문제 해결하기

Gurobi와 같은 최신 솔버는 사용자가 모델을 설정할 때 "웜 스타트" 솔루션을 제공할 수 있도록 합니다. 이 초기 솔루션은 최적화 프로세스를 더 효율적으로 만들어 줍니다. 저희의 선반 휴리스틱으로부터 얻은 솔루션에서 값을 추출하고 모델에서 기대하는 형식으로 솔루션을 변환할 수 있습니다. 기억하세요, 이에는 좌표 뿐만 아니라 총 너비, 높이, 회전 변수 및 겹치는 변수 b_i_j_k도 포함됩니다. 아래의 코드 스니펫을 사용하여 휴리스틱에서 솔루션을 쉽게 변환할 수 있습니다:

heuristic_dict = dict()
for rect in packed_rectangles: 
  index = rect.index
  heuristic_dict[index] = rect

b_values = dict()
for i in I:
  for j in I:
    if i == j:
      continue
    else:
      rect_i = heuristic_dict[i]
      rect_j = heuristic_dict[j]
      
      # b의 초기값을 0으로 설정
      b_values[(i,j,0)] = 0
      b_values[(i,j,1)] = 0
      b_values[(i,j,2)] = 0
      b_values[(i,j,3)] = 0

      # 각 조건을 확인하고 b의 실제 값을 설정
      if rect_i.x + rect_i.width <= rect_j.x:
        b_values[(i,j,0)] = 1

      if rect_j.x + rect_j.width <= rect_i.x:
        b_values[(i,j,1)] = 1

      if rect_i.y + rect_i.height <= rect_j.y:
        b_values[(i,j,2)] = 1

      if rect_j.y + rect_j.height <= rect_i.y:
        b_values[(i,j,3)] = 1   

# x, y 및 r의 솔루션 값을 저장
x_dict = dict()
y_dict = dict()
r_dict = dict()

for i in I:
  REC = heuristic_dict[i]
  x_dict[i] = REC.x
  y_dict[i] = REC.y
  r_dict[i] = 1  # 모든 자산은 회전되지 않음

이제 휴리스틱 솔루션을 추출하고 모델이 예상하는 적절한 형식으로 변환했으므로 이 솔루션을 시작점으로 추가하여 모델을 다시 실행할 수 있습니다. 아래 코드는 새로운 모델을 작성하고 웜 스타트 솔루션을 추가하는 방법을 보여줍니다.

# 이전과 같은 모델
model = gp.Model("Assortment_warm_start", env=env)

x = model.addVars(I, lb=0, ub=top, vtype=GRB.CONTINUOUS, name="x")
y = model.addVars(I, lb=0, ub=top, vtype=GRB.CONTINUOUS, name="y")

R = model.addVars(I, vtype=GRB.BINARY, name='R')

X = model.addVar(lb=0, ub=top, vtype=GRB.CONTINUOUS, name="X")
Y = model.addVar(lb=0, ub=top, vtype=GRB.CONTINUOUS, name="Y")

b_vars = [(i, j, k) for i in I for j in I if j != i for k in K]
B = model.addVars(b_vars, vtype=GRB.BINARY, name="B")

model.setObjective(X*Y, GRB.MINIMIZE)

for i in I:
  model.addConstr(X >= x[i] + WIDTHS[i]*R[i] + (1-R[i])*HEIGHTS[i])
  model.addConstr(Y >= y[i] + HEIGHTS[i]*R[i] + (1-R[i])*WIDTHS[i])

for i in I:
  for j in I:
    if i == j:
      continue
    else:
      model.addConstr(x[i] + WIDTHS[i]*R[i] + (1-R[i])*HEIGHTS[i] <= x[j] + M*(1-B[i,j,0]))
      model.addConstr(x[j] + WIDTHS[j]*R[j] + (1-R[j])*HEIGHTS[j] <= x[i] + M*(1-B[i,j,1]))
      model.addConstr(y[i] + HEIGHTS[i]*R[i] + (1-R[i])*WIDTHS[i] <= y[j] + M*(1-B[i,j,2]))
      model.addConstr(y[j] + HEIGHTS[j]*R[j] + (1-R[j])*WIDTHS[j] <= y[i] + M*(1-B[i,j,3]))
      model.addConstr(B[i,j,0] + B[i,j,1] + B[i,j,2] + B[i,j,3] >= 1)

# 휴리스틱 솔루션을 추가
for var in x:
  x[var].Start = x_dict[var]
  y[var].Start = y_dict[var]
  R[var].Start = r_dict[var]

X.Start = total_X
Y.start = total_Y

for var in B:
  B[var] = b_values[var]

이제 모델이 웜 스타트로 초기화되었으므로 해결할 수 있습니다.

tl = 600
mip_gap = 0.05

model.setParam('TimeLimit', tl)
model.setParam('MIPGap', mip_gap)
model.optimize()

만약 모든 게 예정대로 진행된다면, 최적화 프로세스를 시작하기 위해 사용자가 제공한 솔루션으로부터 시작한다는 솔버의 메시지가 나타날 것입니다. 아래 그림 8과 같이 보일 것입니다.

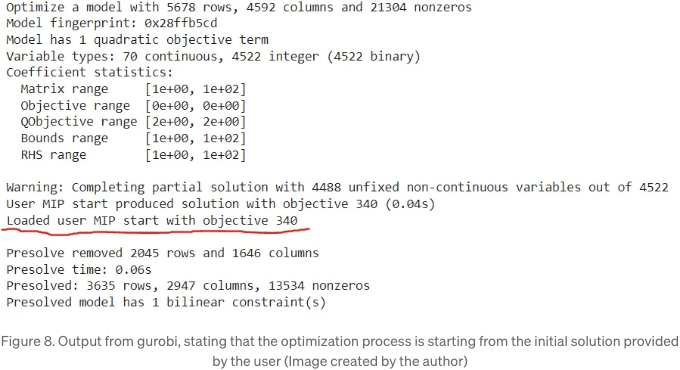
결론

이 글을 마무리하며, 수학적 프로그래밍을 사용하여 2차원 배열 문제를 해결하는 방법에 대한 세부적인 여정을 안내했습니다. 이 문제에 대한 혼합 정수 선형 프로그래밍 공식 및 일부 고전적인 인공 지능을 사용하여 이 문제를 해결하는 방법에 대해 논의했습니다. 또한 이러한 인공 지능에서 얻은 해결책을 우리의 솔버에 대한 초기 설정값으로 사용하는 방법을 다뤘습니다. 이 글이 현재 직무에서 비슷한 도전에 직면한 사람들에게 유용한 자원으로 기여하기를 희망합니다. 그당시 이 지식을 가지고 있었으면 정말 좋았을 텐데, 그럼에도 불구하고 항상 배우는 것은 늦지 않습니다. 이 글에 사용된 코드 전체를 포함한 노트북은 아래 나의 GitHub 저장소 링크에서 찾을 수 있습니다.

이 글이 유익하고 즐거우셨기를 진심으로 바라고 있습니다. 그렇다면, 귀하의 생각을 듣고 싶습니다! 의견을 자유롭게 남겨주시거나 박수 👏로 감사의 의미를 표현해주세요. 그리고 최신 글을 계속해서 받아보고 싶다면 저를 Medium에서 팔로우해보세요. 여러분의 지지와 피드백이 제게 이 흥미로운 분야에서 계속 탐험하고 공유하는 원동력이 됩니다. 읽어 주셔서 감사합니다. 앞으로 더 많은 통찰력을 기대해주세요!

참고문헌

[1] William HP. 수학적 프로그래밍에서 모델 작성. 4판. Chichester: Wiley; 1999
[2] Huang, Y.H., Lu, H.C., Wang, Y.C., Chang, Y.F. 및 Gao, C.K., 2020. 제조 산업의 2차원 커팅 재고 문제에 대한 글로벌 방법론. 비즈니스 및 경영에서 의사결정 과학의 응용, p.167.
[3] Li HL, Chang CT. 조합 문제에 대한 대략적인 글로벌 최적화 방법. 유럽 운영 연구 저널. 1998;105:604–612
[4] Martello S, Vigo D. 2차원 유한 바이너리 패킹 문제에 대한 정확한 해법. 경영 과학. 1998;44:388–399
[5] Chen CS, Sarin S, Balasubramanian R. 특정 조합 문제를 위한 혼합 정수 프로그래밍 모델. 유럽 운영 연구 저널. 1993;65:362–367
[6] Apple, J.M., 및 Deisenroth, M.P., “컴퓨터화된 공장 배치 및 평가 기술 — PLANET”, AIIE 연례 회의 논문집, 1973년 5월, 121.
[7] Buffa, E.S., Armour, G.C., 및 Vollman, T.E., “CRAFT를 사용하여 시설 할당”, 하버드 비즈니스 리뷰, 1964년 3-4월, 130.
[8] Seehof, J.M., and Evans, W.O., “자동화된 배치 설계 프로그램 (ALDEP)”, 산업 공학 잡지 1967년 12월, 690.

수학적 프로그래밍으로 자산 저장 문제 해결하는 방법