
고등학교 수학 학생에서 박사 후 수준의 최첨단 순수 수학 연구에 이르기까지 여정을 거친 개발자로서, 이러한 다른 교육 수준에서 뇌가 어떻게 작동하는지에 대한 한 가지 중요한 차이점을 강조하고 싶습니다.
고등학교 학생들은 수학을 연습할 때 일반적으로 특정 문제에 자신들의 교과지식을 적용하여 학습합니다. 이 문제들은 일반적으로 특정 값, 객체 또는 함수와 관련이 있습니다. 예를 들어, 고등학교 학생들은 보통 정수, 실수 또는 복소수, 또는 정수 다항식과 작업할 것입니다. 이로써 그들은 전문 수학자가 되기 위해 필요한 지식과 패턴인식을 향상시킵니다.
그러나 완전히 발전된 전문 수학자들은 최대한 일반화하고 추상화하여 생각하는 데 훈련 받습니다. 정수나 확립된 일상적인 숫자 구조와 작업하는 대신, 그들은 그룹, 환, 모듈 또는 체와 같은 추상 대수 구조와 작업합니다. 이는 많은 알려진 보다 구체적인 구조를 포괄하는데, 그 결과로 그들의 결과물은 더 강력해지며 보다 일반적인 구조와 문제에 적용할 수 있게 됩니다.
이 문장은 조금 추상적이에요. 웃음을 포함하기 위해 말장난을 쓰는 걸 용서해주세요. 수학적 통찰을 일반화하는 기회를 잡는다면 더 강력해질 수 있다는 간단한 예시를 보여드리겠어요. 이 옥스퍼드 수학 입학 시험 문제에서 고등학생은 특정 상황에 대해 결론을 내야 하죠. 그러나 접근법의 일반화를 발견하려는 순간에 훨씬 더 일반적인 결론을 내릴 수 있다는 것이 밝혀졌어요. 시험지에서의 문제로 시작해볼게요.
원본 MAT 문제 및 해답

미국 독자분들을 위해, '사탕'에 대한 미국식 단어는 '과자'입니다 😊
문제를 적혀 있는 그대로 해결해 보겠습니다. 그리고 우리의 해결책에 대해 일반화할 수 있는 부분이 있는지 살펴보겠습니다.
(i)부분에서 우리는 어떤 날이든 미리암이 이득을 얻는 것을 알 수 있습니다. 따라서 미리암은 여행 중 첫 15일이 맑은 날이 되도록 하여 이득을 극대화할 것입니다. 따라서 첫 15일 동안 이득을 한개씩 더 해가며, 총 15일 후에는 15개의 숫자의 합, 즉 ½ × 15 × 16 = 120개의 사탕을 얻을 것입니다. 그리고 나머지 15일 동안은 하루에 15개의 사탕을 받을 것이며, 이로써 추가로 15²= 225개의 사탕을 얻게 됩니다. 따라서 미리암의 가장 많은 사탕의 개수는 120 + 225 = 345개가 됩니다. (부모님은 이곳에서 수학을 한 결과에 확실히 경악할 것입니다)! 반대 경우는 미리암이 가장 적은 사탕의 수를 받는 경우입니다. 즉, 처음 15일이 비 오는 날이고 사탕을 전혀 받지 않으며, 마지막 15일이 맑은 날이고 각각 하나의 사탕을 받는 경우로, 이 경우 총 120개의 사탕을 받게 됩니다.
(ii)부분에서, 처음 15일이 맑은 날인 경우 아담은 이 날들에 사탕을 전혀 받지 않습니다. 그런 다음 16일차에 16개의 사탕을 받고, 17일차에 17개의 사탕을 받는 식으로 30번째 날에 30개의 사탕을 받게 됩니다. 따라서 아담이 받는 총 사탕의 수는 16부터 30까지의 모든 정수를 더한 것으로, 이는 미리암과 마찬가지로 345개가 됩니다. 처음 15일이 비 오는 날인 경우, 아담은 1일차에 1개의 사탕을 받고, 2일차에 2개의 사탕을 받는 식으로 15일차에는 15개의 사탕을 받습니다. 그 후에는 사탕을 받지 않습니다. 따라서 이 경우 아담이 받는 사탕 역시 처음 15개의 정수를 더한 값인 120개입니다.
(iii)부분에서, 우선 하루가 비 오는 날이고 다음 날이 맑은 날인 미리암의 경우를 살펴보겠습니다. 그리고 k를 이 비 오는 날을 포함하여 지난 휴가 중에 발생한 맑은 날의 수라고 가정합니다. 그러면 오늘이 미리암이 총 사탕을 받는 데에 k개에 기여할 것이고, 내일은 k+1개를 기여할 것입니다. 따라서 오늘과 내일 모두 미리암의 총 사탕에 2k+1개를 기여합니다. 이제 이 두 날을 바꿔 봅시다. 그러면 오늘이 미리암에게 k+1개의 사탕을 기여할 것이고, 내일 또한 k+1개를 기여하므로, 따라서 이 두 날은 미리암의 총 사탕에 2k+2개를 기여합니다. 이 교환이 다른 날들이 미리암의 총 사탕에 기여하는 데에 영향을 주지 않는다는 것에 유의하면, 이 교환은 미리암의 총 사탕을 한 개 더 늘어나게 합니다. 아담의 경우에도 동일한 방법을 사용하면, k일이 비 오는 날이라고 가정하고 그 다음 k+1일이 맑은 날인 경우를 생각해봅시다. 그러면 k일이 아담의 총 사탕에 k개를 기여하고 k+1일이 0을 기여하는데, 따라서 총 k개를 기여할 것입니다. 이들을 교환하면, k일이 0을 기여하고 k+1일이 k+1을 기여하므로, 총 기여하는 양은 k+1개가 됩니다. 따라서 아담의 경우에도 이 교환으로 인해 한 개의 사탕을 더 받습니다.
(iv) 부분에서는 실제로 지금까지 한 작업을 약간의 일반적화하도록 유도받았습니다. 처음 두 부분에서 알 수 있듯이 첫 15일이 비 오는 휴일과 다음 15일이 맑음인 경우, 아담과 미리암이 같은 양의 사탕을 먹는다는 것을 알았습니다. 그러나 여기서 중요한 깨달음은 — 이 시나리오로 시작한다면 — 우리는 점진적으로 인접한 비와 맑은 날을 교환하여 15일 간의 비와 맑은 날의 어떤 구성도 얻을 수 있다는 것입니다. 예를 들어, 주어진 구성에서 첫 맑은 날이 16일인 경우, 우리는 초기 시나리오로 돌아가서 15일과 16일을 교환합니다. k가 15이면, 14일과 15일을 교환하고, 이렇게 반복하여 k에 첫 맑은 날을 배치합니다. 그런 다음 j k 위치에 다음 맑은 날을 배치하고, 이를 반복합니다. 이제 (iii)부분에서 어떤 교환 시리즈도 미리암과 아담의 합계에 동일한 영향을 준다는 것에 주목합니다. 따라서 그들은 같은 총 사탕 양으로 시작하며, 우리가 만드는 모든 인접한 교환은 그들의 총 사탕에 동일한 영향을 미치므로, 미리암과 아담이 같은 총 사탕 양을 가질 것이라고 결론지을 수 있습니다. 15일 동안 비와 맑은 날이 있는 휴일에 대해서도 마찬가지입니다. 그럼 이 내용으로 마칩니다.
여기서 멈추는 이유가 있을까요?
우리가 위에서 한 내용을 일반화하여, 휴일이 얼마나 길든 날씨가 어떻든 상관없이 미리암과 아담이 가질 사탕 양의 차이를 계산하는 데 기회를 발견했나요? 다시 한번 살펴보고, 이번에는 계산을 추상화해 봅시다!
휴일이 30일이고 15일 동안 비가 오고 15일 동안 맑은 날이라는 것 대신에, 휴일이 q일이라고 가정하고 k ≤ q인 비 오는 날이 k개이고 맑은 날이 q-k개인 경우를 생각해 봅시다.
위의 방법에서 알 수 있듯이, 우리는 k일 동안의 비가 내린 날이 모두 달의 시작부터인 것으로 가정할 수 있습니다. 인접한 비 오는 날과 맑은 날을 교환하는 일련의 작업으로 이를 통해 어떤 구성도 유도할 수 있고, 이것이 어린이들이 받는 사탕의 총 수를 변경하지 않음을 알 수 있습니다. 따라서 k일 동안 비가 내린 다음 q-k일 동안 맑은 날이 있는 이 초기 구성에서 사탕의 차이를 계산하는 것으로 충분합니다.
아담의 경우, 이 구성에서 그는 0개의 사탕에서 시작하여 처음 k일 동안 매일 추가로 한 개의 사탕을 받은 후 더 이상 사탕을 받지 않게 됩니다. 따라서 아담은 다음과 같은 수의 사탕을 받게 됩니다:
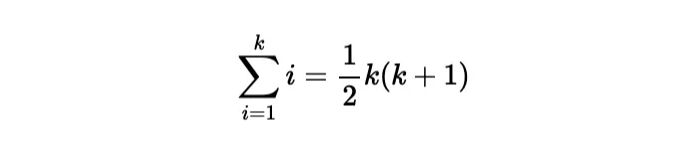
미리암의 경우, 처음 k일 동안은 사탕을 받지 않다가 k+1일에 한 개의 사탕을 받은 후 마지막 날(q일)까지 각각의 추가적인 날마다 한 개의 사탕을 받습니다. 따라서 미리암은 다음과 같은 수의 사탕을 받게 됩니다:
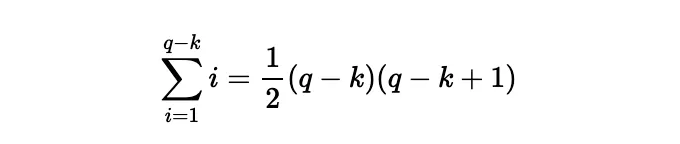
When we subtract these two and perform some algebraic simplification, we obtain a general expression for the difference in the number of sweets received by Miriam and Adam for any holiday lasting q days with k ≤ q rainy days:
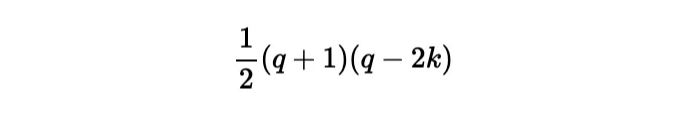
It's clear from this equation that for holidays with an equal number of rainy and sunny days (i.e., q = 2k), the difference in sweets is zero, and both children will receive the same number of sweets. Furthermore, the number is positive when there are more sunny days than rainy days (favoring Miriam), and negative when there are more rainy days than sunny days (favoring Adam).
시험 문제의 이 추상화에 대해 어떻게 생각하셨나요? 자유롭게 의겢하여 주세요.