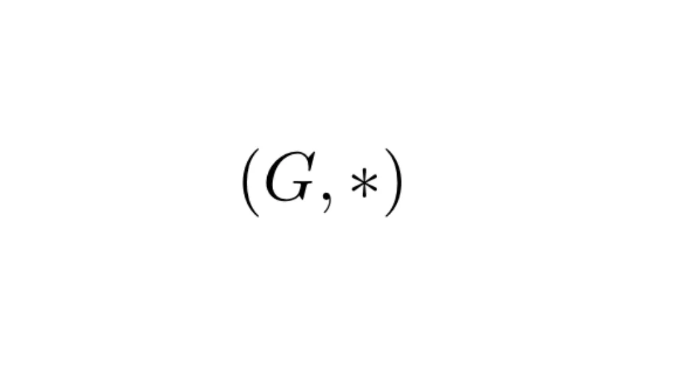
30년이나 40년 전에 열정적이고 재능 있는 고등학교 수학 학생이었다면, 당신이 교과과정의 일환으로 기초 그룹 이론을 공부했을 확률은 거의 확실했습니다. 안타깝게도 이제는 이러한 경우가 많지 않습니다. 많은 고등학교 교육과정에서 그룹 이론이 제외되었으며, 오늘날 많은 사람들은 수학 관련 학과를 전공할 때 처음으로 마주치게 됩니다.
이 점이 안타깝습니다. 그룹 이론은 대수학자처럼 생각하는 방법에 대한 훌륭한 입문입니다. 이러한 사고 방식을 통해 조직적이고 체계적이게 이산적이고 추상적인 객체를 처리할 수 있으며, 이는 고급 수학을 공부하는 데 필수적인 기술이자 삶 전반에서 극도로 유용한 기술입니다. 이러한 방식으로 생각하는 데는 익숙해지기에 시간이 필요하며, 학교에서 조금이라도 경험이 있는 사람들은 학위 수준에서 수학을 공부할 때 더 빨리 적응할 것입니다.
저는 1988년 케임브리지 대학 입학 시험지에서 이 문제를 발견했으며, 이 문제가 내 주장을 훌륭하게 설명해 주는 사례라고 생각합니다. 만약 이 문제에 대해 적절한 순서와 논리적으로 생각할 수 있다면, 해결책은 깔끔하고 매우 우아할 것입니다. 그러나 대수학자처럼 생각하는 방법에 대한 훈련이 없다면, 이 문제에 대처하는 데 어려움을 겪을 것입니다.
문제를 제시하기 전에 옛날에 고등학생들이 배우던 작은 양의 군 이론을 소개해드릴게요 😊
그룹이란 무엇인가요?
그룹은 수학에서 보는 일부 공통 구조를 추상화하고 일반화하는 방법입니다. 간단한 예로, 정수 집합을 살펴봅시다. 이 집합에서 덧셈 연산을 살펴보겠습니다. 정수와 이 연산에 대한 몇 가지 특성이 있습니다. 이러한 특성들은 당연하게 여기지만, 그들이 작동하고 유용성과 관련이 있습니다. 여기 몇 가지 특성이 있습니다:
- 정수는 덧셈에 대해 닫혀 있습니다. 즉, 모든 두 정수를 더하면 다른 정수가 나옵니다.
- 정수는 덧셈에 대해 결합적입니다. 즉, 세 개의 정수 a, b 및 c가 있을 때 a + (b + c) = (a + b) + c 가 성립합니다.
- 항등원인 0(영)이 존재합니다. 이 정수는 다른 어떤 정수에 더해져도 같은 정수를 반환합니다. 따라서 모든 정수 a에 대해 a + 0 = 0 + a = a 가 성립합니다.
- 임의의 정수 a에 대해 역원 -a가 존재합니다. 이는 정수와 그 역원을 아무 순서로 더하면 항등원 0이 나온다는 것을 의미합니다. 즉, 모든 정수 a에 대해 a + (-a) = (-a) + a = 0 가 성립합니다.
이러한 속성들을 일반 대수 구조를 정의하는 추상화된 개념으로 정의할 수 있습니다.
그룹은 다음과 같은 조건을 만족하는 객체 G로 이루어진 집합과 해당 객체들에 대한 연산인 *을 함께 하는 것으로 정의됩니다:
- g, h가 G에 속한다면 g*h도 G에 속합니다.
- 임의의 g, h, k가 G에 속할 때, g*(hk) = (gh)*k가 성립합니다.
- G에는 항등원인 e가 존재하며, 모든 g ∈ G에 대해 ge = eg = g가 성립합니다.
- 모든 g ∈ G에 대해 역원 g^(-1)이 존재하며, g * g^(-1) = g^(-1) * g = e가 성립합니다.
그룹이라는 개념은 우리가 일상 생활에서 유용하게 활용하는 수학적 구조를 추상화하는 방법으로 개발되었지만, 이 정의가 소개된 이후 몇 세기 동안, 수학자들은 이러한 속성을 따르며 거대하고 완전히 믿기 어려운 방식으로 유한 그룹을 형성하는 놀라운 구조들을 발견해왔습니다. 예를 들어, 몬스터 그룹은 1970년대에 발견되었으며 808,017,424,794,512,875,886,459,904,961,710,757,005,754,368,000,000,000개의 원소로 구성되어 있습니다.
문제
여기는 1988년 케임브리지 대학 입시시험의 한 문제입니다. 만약 원하신다면, 제가 풀이를 보여주기 전에 먼저 도전해보세요. 그룹에는 하나의 연산만 정의되어 있기 때문에 그룹에서 대수를 다룰 때 연산 표기를 생략하는 것이 일반적이며 편리합니다. 그렇기 때문에 gh는 단순히 gh로 쓰이고 gg는 g²로 쓰입니다.

나의 풀이 — 파트 (i)
우리는 o(g) = n이라고 말을 들었습니다, 따라서 g^k = e인 더 작은 양수 정수 k ` n은 없습니다. 따라서 g^N = e이면 N ≥ n이어야 합니다.
우리는 숫자 N을 N = kn + j로 쓸 수 있습니다. 여기서 k ≥ 1이고 0 ≤ j ` n입니다. 그러면 다음을 말할 수 있습니다.
| g^j | g^(n+j) | g^(2n+j) | ... | g^((k-1)n+j) |
|---|---|---|---|---|
| g^0 | g^n | g^(2n) | ... | g^((k-1)n) |
그러나 우리는
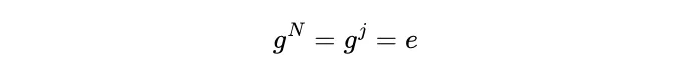
그리고 0 ≤ j ≤ n이기 때문에 j = 0이어야 합니다. 왜냐하면 o(g) = n이기 때문이죠. 따라서 N = kn이고, 따라서 n은 N으로 나누어집니다.
내 해답 — Part (ii)
이 부분이 더욱 명확해지도록 우리의 연산 표기법을 사용해봅시다. 다음과 같이 말할 수 있습니다:
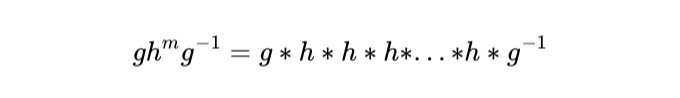
With the h element repeated m times. Now note that:
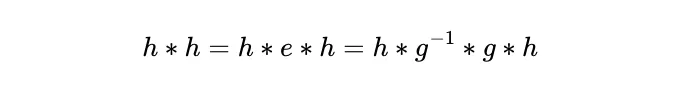
So this means we can make the following replacement:
<img src="/TIL/assets/img/2024-07-12-HowToThinkLikeAnAlgebraist_6.png" />
h가 처음과 끝을 포함해 m번 나타납니다. 이제 우리가 이것을 원래 식에 넣으면
<img src="/TIL/assets/img/2024-07-12-HowToThinkLikeAnAlgebraist_7.png" />
오른쪽에 m번 반복되어 있습니다. 따라서 필요한 결과를 얻을 수 있습니다.
나의 해결책 — Part (iii)
주어진 정보를 사용하면:
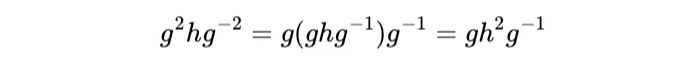
이제 우리가 이전 부분에서 얻은 결과를 사용해봅시다:
아래와 같이 변경해주셨으면 좋겠습니다.
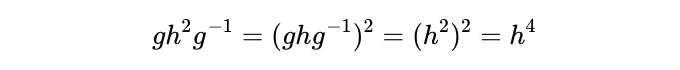
아래의 내용대로 수정해 주십시오.
To find o(h), we can use the given fact that g⁵ = e. Consider the following logic:
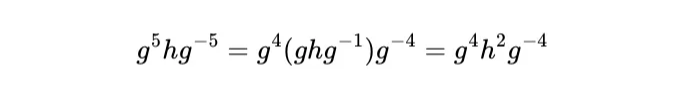
아래와 같이 결과를 사용하여 이를 반복할 수 있습니다.
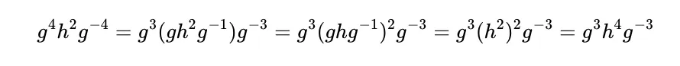
유사한 논리를 사용하여 계속하여 이 패턴을 유지하면 다음과 같은 결론을 내릴 수 있습니다:
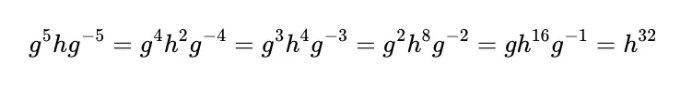
하지만 우리는 g⁵ = e임을 알고 있으므로, 다음과 같이도 말할 수 있습니다:
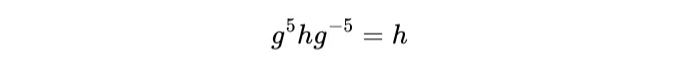
따라서:
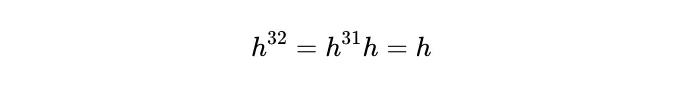
그래서:
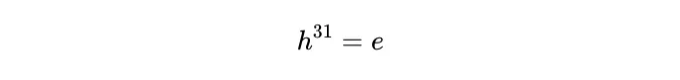
이제, Part (i)를 사용하면 h의 순서는 31로 나누어져야 합니다. 그런데 31은 소수입니다. 따라서 o(h) = 31입니다.
그룹 이론에 대한 소개 어땠나요? 자유롭게 의견을 남겨주세요!