TIL

시계열 데이터에서 기본 모델 적용하는 방법

시계열 데이터에서 기본 모델 적용하는 방법
TILPosted On Jul 12, 20247 min read

이미지

데이터 수집을 완료했습니다. 사업 케이스를 개요하고 후보 모델(예: 랜덤 포레스트)을 결정했으며, 개발 환경을 설정하고 키보드에 손을 대었습니다. 이제 시계열 모델을 구축하고 훈련할 준비가 되었습니다.

잠깐만요 - 바로 시작하지 마세요. 랜덤 포레스트 모델의 훈련 및 테스트를 시작하기 전에 먼저 베이스라인 모델을 훈련해야 합니다.

베이스라인 모델이란 무엇인가요?

기준 모델은 최종적으로 더 복잡한 머신 러닝 모델을 구축하기 위한 기준이 되는 간단한 모델입니다.

데이터 과학자들이 기준 모델을 만드는 이유는:

  • 기준 모델을 통해 더 복잡한 모델의 성능을 어느 정도 예측할 수 있습니다.
  • 기준 모델의 성능이 좋지 않을 경우, 데이터 품질에 문제가 있을 수 있음을 나타낼 수 있습니다.
  • 기준 모델이 최종 모델보다 더 나은 성능을 보일 경우, 해당 알고리즘, 특성, 하이퍼파라미터 또는 다른 데이터 전처리에 문제가 있을 수 있습니다.
  • 기준 모델과 복잡한 모델이 비슷하게 성능을 보인다면, 복잡한 모델이 더 세밀한 조정이 필요하다는 것을 나타낼 수 있습니다. 또한, 더 복잡한 모델이 필요하지 않을 수도 있고, 보다 간단한 모델이 충분할 수도 있습니다.

보통 기준 모델은 이동 평균 모델과 같은 통계 모델이거나, 대상 모델의 간단한 버전일 수 있습니다. 예를 들어, Random Forest 모델을 학습할 예정이라면 먼저 기준으로 Decision Tree 모델을 학습시킬 수 있습니다.

시계열 데이터의 기준 모델

시계열 데이터에 대해 기준 모델로 인기 있는 옵션이 몇 가지 있습니다. 이 중에서 함께 공유하고 싶어요. 이 두 가지 모두 데이터의 시간순서를 전제로 하고 데이터의 패턴에 따라 예측을 수행하기 때문에 잘 작동합니다.

단순 예측

단순 예측은 가장 간단한 방법입니다 — 다음 값은 이전 값과 동일하다고 가정합니다.

날씨를 예측해보려는 모델을 구축 중이라고 가정해 봅시다. 이미 'Date'와 'TemperatureF' 두 개의 열이 적어도 포함된 데이터프레임 df를 불러왔다고 상정할게요. 이를 Python으로 구현하기 위해 먼저 타임스탬프와 타겟 변수를 분리하고 학습 및 테스트 세트로 분할하세요.

import numpy as np 

# 분할 인덱스 정의
split_time = 1000

# 타겟 배열과 시간/날짜 배열 분리
series = np.array(df['TemperatureF'])
time = np.array(df['Date'])

# 학습 및 테스트 세트 나누기
time_train = time[:split_time]
time_test = time[split_time:]

series_train = series[:split_time]
series_test = series[split_time:]

이제 데이터를 준비했으므로, 순진한 예측을 계산할 수 있어요.

# 순진한 예측은 단순히 시리즈를 1만큼 이동합니다
naive_fcst = series[split_time - 1: -1]

결과를 시각화하고 테스트 세트에서 나이브 예측이 어떻게 수행되는지 확인하기 위해 plotly 그래프 개체를 사용할 수 있습니다:

import plotly.graph_objects as go

fig = go.Figure([
        go.Scatter(x=time_test, y=series_test, text='true', name='true'),
        go.Scatter(x=time_test, y=naive_fcst, text='pred', name='pred'),
    ])

fig.show()

여기 제 결과물입니다:

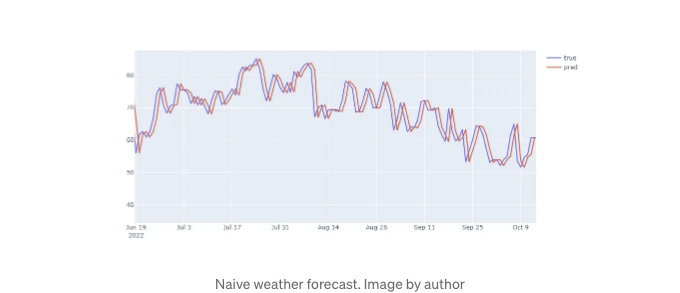
마지막 단계는 후에 벤치마킹에 사용할 메트릭을 계산하는 것입니다. 선택할 메트릭은 특정 문제에 따라 다를 것이지만 MSE 및 RMSE를 계산하는 방법은 다음과 같습니다:

from sklearn.metrics import mean_squared_error

mse = mean_squared_error(series_test,naive_fcst)
rmse = mean_squared_error(series_test,naive_fcst,squared=False)

print(“MSE:”, mse)
print(“RMSE:”, rmse)

이동 평균 예측

이동평균(MA) 베이스라인 모델은 다음 데이터 포인트를 바로 이전 n개의 데이터 포인트의 평균으로 예측합니다. n의 값은 사용자에 달려있어요—일반적인 이동평균에는 30일 이동평균, 60일, 90일, 180일 등이 있습니다. 또한 사용 사례 및 분야에 따라 달라집니다. 주식 시장에서는 종종 21, 50, 100 및 200을 사용합니다. 게다가, 최종 모델로 30일을 예측할 것이라는 것을 알고 있다면 30일 이동평균을 사용하여 베이스라인을 테스트하는 것이 좋습니다.

특정 문제와 목표 결과에 대해 일반적으로 사용되는 이동 평균을 조사해보는 것이 중요합니다.

이를 Python으로 구현하려면, 이전과 동일한 데이터 구조(시간 및 시리즈)를 유지한 채 다음을 수행하십시오.

먼저, 전체 데이터셋에 대한 예측을 생성하십시오.

# 리스트 초기화
forecast = []
window_size = 30

# 윈도우 크기를 기반으로 이동 평균 계산
for time in range(len(series) - window_size):
    forecast.append(series[time:time + window_size].mean())

# 넘파이 배열로 변환
forecast = np.array(forecast)

다음으로 이동 평균 예측에서 테스트 세트를 분리하세요. 원래의 테스트 세트와 일치시키기 위해 window_size만큼 예측 배열을 이동할 겁니다.

moving_avg = forecast[split_time - window_size:]

이전과 같이 결과를 시각화해서 표시해주세요.

fig = go.Figure([
        go.Scatter(x=time_test, y=series_test, text='true', name='true'),
        go.Scatter(x=time_test, y=moving_avg, text='pred', name='pred'),
    ])

fig.show()

이렇게 보이도록 표 태그를 마크다운 형식으로 변경해보세요.

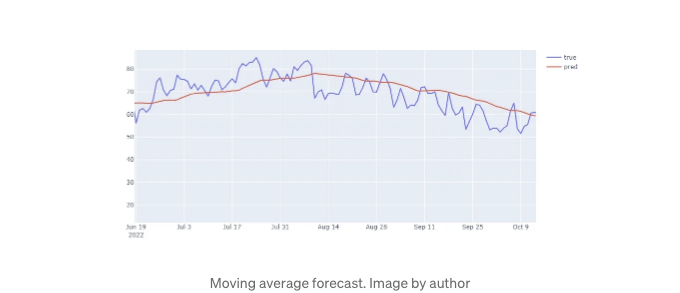
Moving Average Chart

에러 메트릭을 얻으려면, 이전과 같은 과정을 따르되 moving_avg 배열을 사용하면 됩니다.

mse = mean_squared_error(series_test, moving_avg)
rmse = mean_squared_error(series_test, moving_avg, squared=False)

print("MSE:", mse)
print("RMSE:", rmse)

주의 사항 + 결론

"예측"이라는 단어를 사용했지만, 사실 미래를 예측한 것은 아니에요. 저는 train test split을 했기 때문에 테스트 세트에서 예측을 할 때 이미 날짜별 이전 값을 가지고 있었거든요. 만약 앞으로 30일을 예측하려고 한다면, 진정한 naive 예측은 다음 30일이 마지막 날이나 마지막 데이터 포인트와 똑같다고 가정할 것이에요. 이는 수평선 예측으로 이어질 거에요. 이와 마찬가지로 이동평균에도 적용돼요. 그래서 이러한 기술들은 실제로 오랜 기간을 예측하기에는 최적적이지 않아요. 그러나 이러한 기법들은 여전히 기준을 설정하고 최종 모델에서 괜찮은 성능이 어떤 것인지를 평가하는 데 유용해요.

기준 모델은 코드의 타당성을 점검하고 최종 모델이 데이터셋에서 신뢰성 있게 예측할 수 있는 능력을 추정하는 좋은 방법을 제공해요. 데이터 오류를 탐지하고 최종 모델 선택 과정에 도움이 되는 요소일 수 있어요. 다음에 시계열 데이터를 다룰 때는 꼭 먼저 기준선을 설정해보세요.