거리 측정이란 무엇인가요?

아마도 맨해튼 거리 또는 유클리드 거리에 대해 들어보았을 것입니다. 이들은 두 주어진 데이터 포인트가 얼마나 멀리 떨어져 있는지 (또는 얼마나 다른지)에 대한 정보를 제공하는 두 가지 다른 측정 기준입니다.

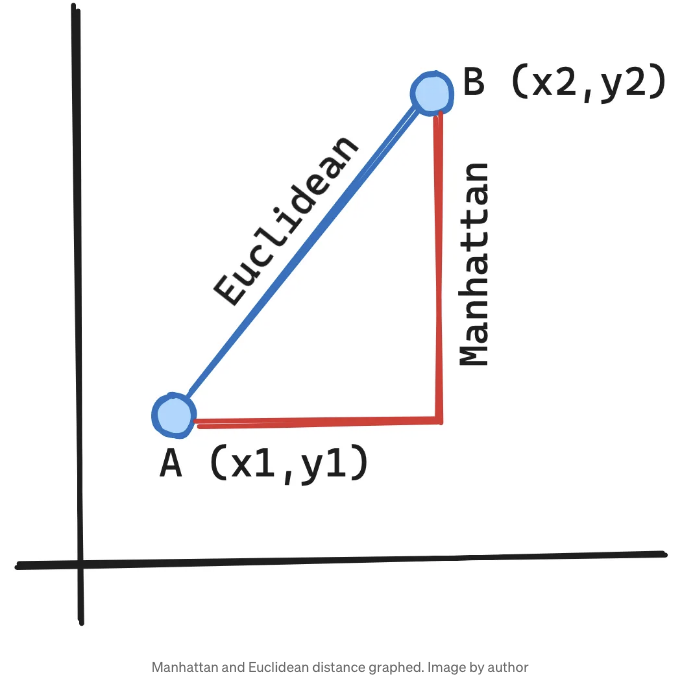
간단히 말해서, 유클리드 거리는 점 A에서 점 B까지의 최단 거리입니다. 맨해튼 거리는 x와 y 좌표 간의 절대적인 차이들의 합을 계산하고, 대각선 방향으로 움직일 수 없고 위, 아래, 왼쪽 또는 오른쪽으로만 이동할 수 있는 격자 상에 위치한 것처럼 두 점 사이의 거리를 찾습니다.

거리 측정 항목은 종종 k-평균 클러스터링과 같은 클러스터링 알고리즘의 기초를 이룹니다. 이 알고리즘은 유클리드 거리를 사용합니다. 데이터 포인트 간의 유사성 또는 차이를 먼저 알아야 하므로 이 점이 타당합니다.

2점 사이의 거리 계산하기

이 프로세스를 보여주기 위해 유클리드 거리를 사용한 예제를 통해 시작하겠습니다.

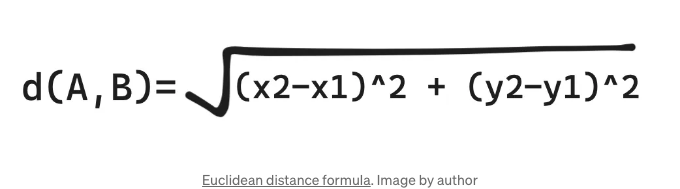
위에 그린 차트를 사용하면 점 A의 좌표가 (50,50)이고 점 B의 좌표가 (300,500)이라고 가정해 봅시다:

d(A,B) = sqrt ((300-50)^2 + (500-50)^2))
d(A,B) = sqrt (62,500 + 202,500)
d(A,B) ≈ 514.78

정말 간단하죠. 이제 Python 데이터 세트에서 데이터프레임을 사용하여 2개의 데이터 포인트(행) 사이에 유사도 점수를 계산하고 싶다면 어떻게 해야 할지 살펴봅시다.

인구 조사 데이터에서의 거리 (Distances in Census Income data)

앞으로 제 모든 예시를 설명하는 데에 UCI Machine Learning Repository에서 제공하는 인구 조사 소득 데이터 세트 (CC BY 4.0)를 사용할 것입니다.

이 데이터 세트는 다양한 인구 특징(나이, 인종, 성별, 직업 등)와 개인이 '$50K 미만' 또는 '$50K 이하'의 소득을 갖고 있는지를 나타내는 바이너리 대상 변수를 가지고 있는 분류 데이터 세트입니다.

이 데이터 세트를 통계 작업에 사용하지는 않겠지만, 유사한 특징을 가진 데이터 포인트 간에는 타겟 변수에 대한 유사성도 보일 수 있기 때문에 거리 측정 지표를 시연하는 데 좋은 예시가 됩니다.

이 데이터를 직접 가져오려면 다음 코드를 실행하세요:

from ucimlrepo import fetch_ucirepo

# 데이터셋 불러오기
census_income = fetch_ucirepo(id=20)

# 데이터 (판다스 데이터프레임 형태)
X = census_income.data.features
y = census_income.data.targets

# 변수 정보
print(census_income.variables)

이 데이터셋에 포함된 특성 변수 중 하나는 "나이(Age)"입니다. 이 경우 나이는 17세에서 90세까지의 숫자 변수입니다. 다른 숫자 변수로는 "자본이득(Capital gains)"이 있습니다. 이 두 변수는 사람의 총 소득과 관련이 깊을 것으로 예상됩니다.

이제 이 두 열을 가지고 데이터 포인트/행에 대한 거리 추정을 얻을 수 있는지 확인해 봅시다.

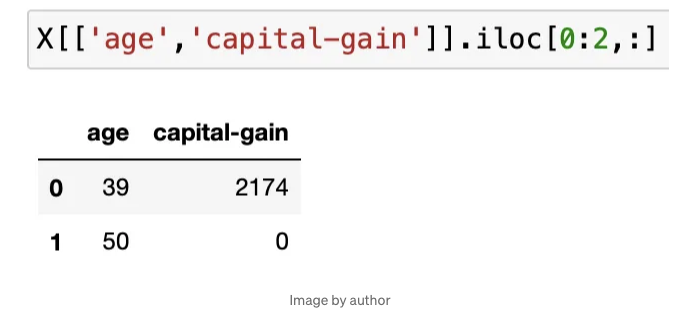
이 두 데이터 포인트 사이의 거리를 찾으려면 위에서 정의한 식에 값을 입력해야 합니다.

각 열은 차원(x 또는 y)이 되고 각 행은 숫자 1 또는 2가 됩니다.

따라서 나이 열은 x가 되고 값(39, 50)은 x1 및 x2가 됩니다. 자본 이득 열은 y1 및 y2 값에 해당합니다.

d(Row1, Row2) = sqrt((50-39)^2 +
(2174-0)^2))

d(Row1, Row2) = 2174.027

총 이동 거리가 자본 이득 열의 차이와 거의 동일한 것을 알 수 있습니다. 이는 값의 연령 범위가 값의 자본 이익 범위보다 훨씬 작기 때문입니다. 따라서 경우에 따라 유클리드 거리를 계산하기 전에 StandardScaler와 같은 것을 사용하여 데이터를 스케일링해야 할 수도 있습니다.

Gower 거리: 방정식에 범주형 변수 추가

이제 만약 이 첫 번째 두 데이터 포인트 사이의 거리를 계산하려면 “workclass”와 “education”과 같은 범주형 변수도 포함해서 어떻게 해야 할까요?

여기서 Gower 거리가 중요합니다. Gower 거리는 숫자형 및 범주형 특성에 대해 서로 다른 거리 계산을 수행하여 특성간 유사성의 가중 평균을 취하여 2개 데이터 포인트 사이의 점수를 계산합니다.

2가지 범주형 특성 간 유사도 점수를 계산할 때, 식은 매우 간단합니다. 값이 동일한 경우 점수는 1입니다. 다른 경우에는 점수가 0입니다.

두 객체(데이터 포인트) i와 j를 비교할 때, 수치/연속적인 특성 k를 비교하는 경우, 유사도 점수는 다음과 같습니다:

[ \frac{|x_{ik} - x_{jk}|}{R(k)} ]

여기서 R(k)는 특성 k의 범위를 나타냅니다. 값의 차이의 절대값은 범위로 나눠줌으로써 특성을 정규화하고 0과 1 사이의 값으로 얻습니다. (이는 매우 큰 값이 포함된 특성이 방정식을 지배하는 문제를 해결하는 데 도움이 될 것입니다.)

이제 각 feature에 대한 점수가 있으므로, p개의 feature가 있는 두 개의 객체 i와 j에 대한 전체 Gower 거리가 계산됩니다:

… where w(ijk) is the weight for that feature (Default is 1).

Python 구현

파이썬 구현은 배열 내 모든 객체를 서로 비교하여 Gower 거리를 반환하는 행렬을 생성합니다.

파이썬에서 이 작업이 어떻게 이루어지는지 보시려고 작은 예제를 소개하겠습니다. 그리고 이것이 대규모 데이터셋에서 어떻게 작동하는지 살펴보겠습니다.

# 먼저 "pip install gower"를 실행했다고 가정합니다.
import gower
import numpy as np

# 특성 정의
features = ['age', 'capital-gain', 'education', 'workclass']

# workclass 열에 일부 누락된 데이터가 "?" 형태로 포함되어 있기 때문에
# 이를 먼저 제거했습니다.
X = X.loc[X['workclass']!='?']

# 가능한 다른 열에서는 널 값을 제거하고 인덱스를 재설정했습니다.
X.dropna(inplace=True)
X.reset_index(inplace=True)

# 정의된 특성만 선택합니다.
X = X[features]

# 처음 2개 행만 포함하는 작은 데이터프레임 생성
# 이 두 행을 Gower 거리를 사용하여 비교할 것입니다.
small_X = X.iloc[0:2,:]

# 나이 열을 부동 소수점으로 변환합니다. 왜냐하면 자본 이익은 실수이며,
# 숫자 열은 동일한 데이터 유형이어야 합니다.
small_X['age'] = small_X['age'].astype(float)

# gower 거리 행렬 생성
# cat_features는 각 열의 인덱스에 해당하는 목록입니다.
# 0은 열이 숫자임을 나타내고, 1은 범주형임을 나타냅니다. 처음 2개 열 (나이 및 자본 이익)
# 는 0으로 표시되고, 마지막 2개 열 (교육, 직업)은 1로 표시됩니다.
gower.gower_matrix(np.asarray(small_X),cat_features=[0,0,1,1])

gower.gower_matrix를 호출하면 이 배열이 반환됩니다.

array([[0. , 1.5],
       [1.5, 0. ]], dtype=float32)

각 요소는 다음을 나타냅니다:

• 요소 [0,0] = 행 1과 행 1 간의 거리 점수
• 요소 [0,1] = 행 1과 행 2 간의 거리 점수
• 요소 [1,0] = 행 2와 행 1 간의 거리 점수
• 요소 [1,1] = 행 2와 행 2 간의 거리 점수

행 1을 행 1과 비교하면 features 측면에서 동일함을 보여주기 때문에 거리는 0으로 표시됩니다. 행 2를 행 2와 비교한 결과도 마찬가지입니다. 행 2를 행 1과 비교하면 행 1을 행 2와 비교했을 때와 동일한 결과가 나오므로 이 요소에서 점수가 동일합니다.

이제 Gower 거리의 구성 요소를 이해했으니 전체 데이터 세트에 이 gower.gower_matrix 함수를 적용해 봅시다.

# 참고: 인구조사 데이터 집합은 40,000개 이상의 행이 있습니다. 이 작업은 
# 계산 비용이 매우 높을 수 있습니다. 저는 제 자신의 코드에서 이 작업을 
# 첫 5000개 행에 대해서만 실행했지만, 데이터 세트에 따라 다를 수 있습니다.
gower.gower_matrix(np.asarray(X),cat_features=[0,0,1,1])

이렇게 하면 각 행을 모든 다른 행들과 비교한 Gower 거리 점수 행렬이 반환됩니다.

Gower 거리의 효과를 더 테스트하기 위해, 첫 번째 레코드와 가장 유사한 10개 레코드를 해당 특성을 사용하여 찾은 다음, 그들의 대상 값(소득 수준)이 유사한지 확인해 보겠습니다.

# 데이터 세트의 첫 번째 행을 가져와 나머지 데이터와 비교합니다. 상위 10개 값의 인덱스를 반환합니다
gower_topn_index = gower.gower_topn(X.iloc[0:1,:], X.iloc[:,], n = 10)['index']

# 원본 df에서 인덱스를 쿼리합니다
X.iloc[gower_topn_index]

다음은 제 결과입니다:

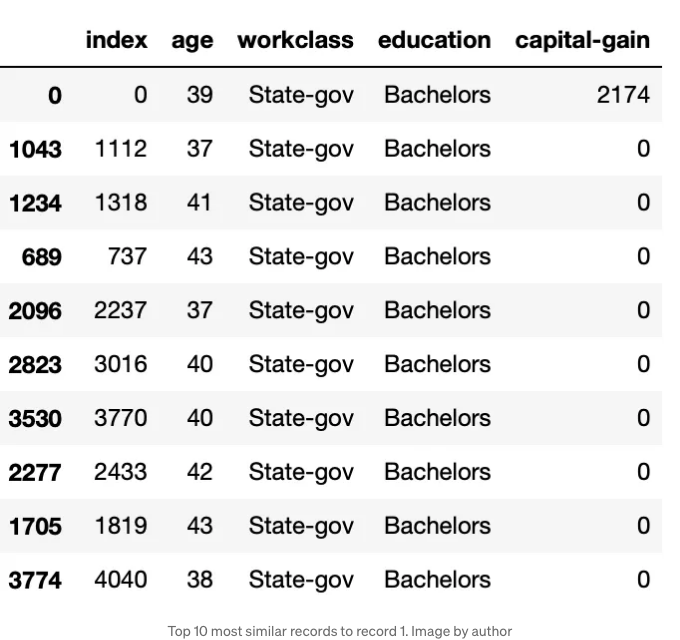
여기서 첫 번째 레코드와 가장 유사한 레코드는 해당 레코드 자체입니다. 이는 Gower가 각각의 레코드를 모든 레코드와 비교하기 때문입니다. 레코드 1과 가장 유사한 상위 n개의 레코드를 가져오고 레코드 1을 제외한 결과를 얻고 싶다면, 초기에 상위 n+1을 가져와 X.iloc[gower_topn_index][1:]를 쿼리하면 해당 최상위 레코드를 결과에서 제외시킬 수 있습니다.

만약 y.loc[gower_topn_index]을 호출하면, 첫 번째 행에 대한 가장 유사한 상위 10개 레코드의 대응하는 타겟 값을 볼 수 있습니다.

여기서 가장 유사한 상위 10개 레코드 중에서 9개 중 6개가 첫 번째 레코드의 수입(≤50K)과 일치했음을 볼 수 있습니다. 9개 중 3개만 일치하지 않고 '50K'를 만들었습니다. 이것은 우리가 4가지 기능만 가지고 있었기 때문에 꽤 괜찮은 결과입니다!

기억해 둘 사항

다른 기계 학습 알고리즘과 마찬가지로 특성을 추가할수록 Gower metric의 정확도가 높아질 것으로 예상됩니다. 이는 레코드가 더욱 유사해진다는 것을 의미합니다. 이때 주의할 점은 범주형 특성이 종종 (연속 값이 아니라 0 또는 1이 될 것이기 때문에 0과 1 사이의 연속적인 값보다) 수치적 특성보다 더욱 중요하다는 것입니다.

이를 균형있게 유지하기 위해 수치적 특성에 더 높은 가중치를 부여하여 실험할 수 있습니다 (weight 인자를 사용).

weight 인자는 cat_features 인자와 유사하게 작동합니다. 여러분은 목록을 전달하고 각 열에 대해 가중치를 지정합니다. 예를 들어 weight = [2, 2, 1, 1]로 설정하면 수치적인 나이와 자본 이득이 포함된 처음 2개 열이 (마지막 2개 범주형 특성보다 최종 거리 공식에서 두 배 높이 가중됩니다.

결론

위에서 볼 수 있듯이, 고워 거리는 혼합 데이터 유형의 기능을 포함하는 두 개체 간의 거리를 계산하는 강력한 메트릭입니다. 이는 단순히 가장 유사한 레코드를 찾는 것에서부터 클러스터링 알고리즘에 사용될 때까지 다양한 용도가 있습니다. 더 많은 정보와 예제는 여기에서 찾을 수 있습니다.

읽어 주셔서 감사합니다