| 인공지능 | 컴퓨터 비전 | 전처리 |

Python에서 모폴로지 연산을 어떻게 구현하는지 및 왜 디지털 이미지 처리에서 중요한지에 대해 설명하는 가이드입니다.
이전 시리즈의 기사는 다음과 같습니다:
형태학 소개
형태학(가끔 수학적 형태학으로도 불립니다)은 이웃 처리의 한 분야로 여겨질 수 있습니다. 1964년 Georges Matheron과 Jean Serra에 의해 개발되었으며, 광물 단면의 특성을 정량화하기 위해 고안되었지만 다른 다양한 응용 분야에서도 가치가 있다는 것이 입증되었습니다. 일반적으로 형태학은 이미지에 일관된 노출이 없는 경우에 발생하는 노이즈를 제거하는 데 사용할 수 있습니다. 실제로 형태학은 역처리로 얻은 바이너리 이미지와 매우 잘 작동하지만(하지만 그레이스케일 이미지에서도 사용할 수 있습니다).
예를 들어, 임계 처리 후 몇 가지 상황이 발생할 수 있고, 이를 형태학으로 해결할 수 있습니다.

여기서 나는 히트 또는 핏 연산, 팽창, 침식을 적용했는데, 이에 대해 자세히 알아볼 것이다.
형태학은 다양한 흥미로운 응용 프로그램을 갖고 있습니다. 예를 들어 광학 문자 인식(OCR)의 전처리 단계로 사용되며, 바코드 및 자동차 번호판은 감지하는 데 사용됩니다. 형태학 연산은 간단하고 계산 비용이 적고 결합하여 효율적으로 사용할 수 있어 시간과 계산 자원을 절약할 수 있습니다. 실제로 여러 가지 작업을 수행하기 위해 복잡한 알고리즘이 필요하지 않을 때가 많으며, 적은 고급 기술도 우아하고 효율적인 솔루션으로 이어질 수 있습니다. 또한, 이러한 연산은 다양한 컴퓨터 비전 알고리즘에서 매우 유용하며 실제로 학습할 가치가 있습니다.
형태학

임계처리는 전역 작업으로 (이미지의 모든 픽셀에 대해) 지역 위치를 고려하지 않고 수행되며, 결과적으로 과소 세분화 또는 과대 세분화된 영역을 유발할 수 있습니다.
대신, 형태학은 이웃 처리와 비슷하게 적용됩니다. 이 경우에는 값이 아닌 모양이 중요합니다 (상자 모양 커널은 날카로운 모서리를 보존하고 둥근/디스크 모양 커널은 모서리를 둥글게 만듭니다).
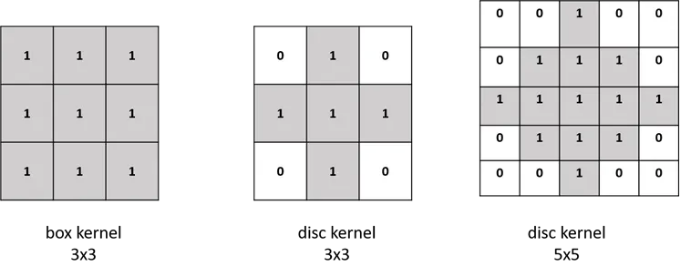
이 커널은 이미지에있는 객체 (또는 요소)에만 적용됩니다. 따라서 커널이 클수록 이미지에 미치는 영향도 커집니다. 이러한 절차는 일반적으로 1이 전경을 나타내고 0이 배경을 나타내는 바이너리 이미지에서 수행됩니다.
맞추기와 맞추기
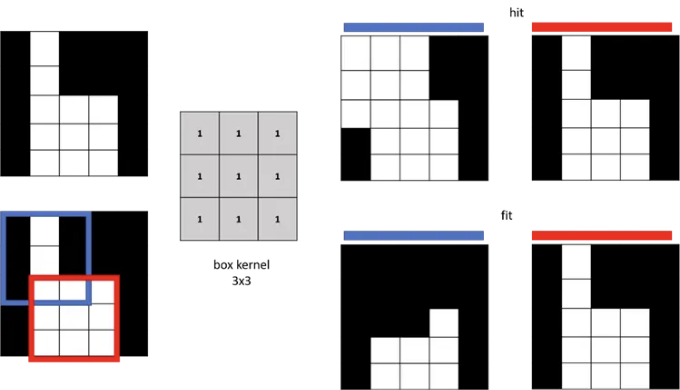
이 알고리즘에서는 위에서 본 것과 같은 모양의 커널을 특정 위치에 놓은 다음 커널에 의해 커버되는 픽셀의 값을 고려합니다. 아이디어는 커널을 고려할 때, 특정 위치에있는 픽셀이 커널에도 1이면 1로 설정하려는 것입니다 (이를 '맞춤'이라고 함). 일치하는 경우 출력 이미지의 픽셀이 1로 설정됩니다. 맞춤 (또는 맞춤)에서 이미지 전체를 스캔하는 것이 아니라 특정 위치와 커널을 선택하고 커널 및 해당 위치의 픽셀의 일치 여부를 확인합니다.
맞춤의 경우에는 커널에있는 것처럼 동일한 위치의 모든 픽셀이 1인지 확인합니다 (참이면 이미지가 맞는 것입니다). 모든 픽셀에 대해 일치하는 경우, 모든 픽셀을 출력 이미지에서 1로 설정하고, 그렇지 않은 경우 모두 0으로 설정합니다. 아래 두 위치에 맞춤 또는 맞춤을 적용합니다:
팽창과 침식
전체 이미지에 히트를 적용하는 것을 '팽창'이라고 합니다. 왜냐하면 그 이미지의 요소들이 변환 후에 크기가 증가하기 때문입니다. 또한, 작은 구멍이 닫히고 일부 객체가 병합됩니다. 증가량은 커널 요소의 크기에 따라 달라지거나, 대안으로 작은 커널을 반복적으로 적용할 수 있습니다. 문제는 잡음이 있는 객체도 확대될 수 있다는 것입니다. 커널 k를 사용한 방정식은 다음과 같습니다:
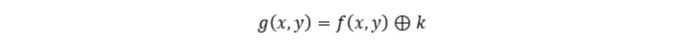
⊕은 벡터 하위 공간의 합을 나타냅니다.
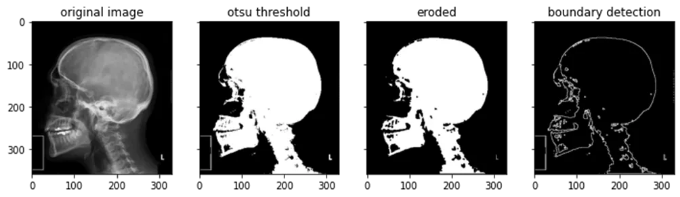
말했듯이, 커널 크기는 영향을 미치며 작은 커널을 반복적으로 적용할 때 영향이 유사합니다 (예: 6x6 커널은 3x3 커널을 2배 적용한 것과 유사한 효과를 줍니다). 이미지에 다른 커널의 효과를 시도해 보겠습니다. 우선 이전 튜토리얼에서 언급했던대로 이미지에 Otsu의 임계값 처리를 적용한 이미지로 시작하겠습니다 (이는 일정 임계값 이상인 픽셀이 255 또는 흰색이 되고 나머지는 0인 바이너리 이미지를 반환합니다).
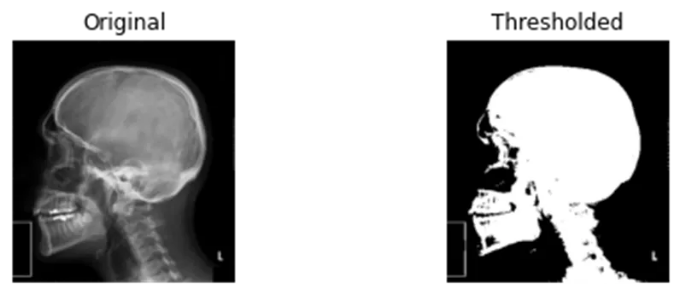
그런 다음 이 바이너리 이미지에 다양한 커널 크기와 팽창을 적용합니다:
# 확장
from scipy import ndimage
from skimage.filters import threshold_otsu
from skimage.morphology import disk
from skimage.morphology import erosion
fig, axes = plt.subplots(ncols=4, nrows=1, sharex=True, sharey=True, figsize=(12, 5))
image = im
thresh = threshold_otsu(image)
binary = image > thresh
dilated = ndimage.binary_dilation(binary, structure=np.ones((3,3)))
dilated1 = ndimage.binary_dilation(binary, structure=np.ones((5,5)))
dilated2 = ndimage.binary_dilation(binary, structure=np.ones((9,9)))
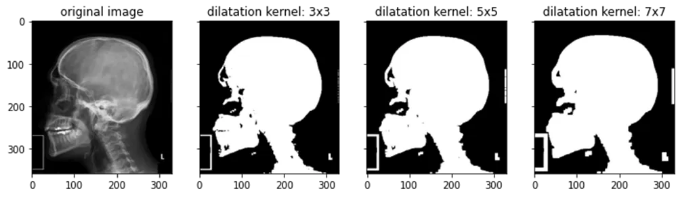
물체가 커지고 이미지의 구멍이 메꿔지며 일부 잡음 요소가 확대되는 것을 알 수 있습니다.
침식은 확장과 정반대입니다. 이 경우에는 모든 이미지에 대해 맞추고 있습니다. 효과는 객체 크기의 일반적인 축소와 작은 객체의 제거로 이어집니다. 더불어 종종 더 큰 객체가 더 작은 객체로 분할됩니다. 우리는 잡음을 제거하지만 관심 대상 객체는 파손됩니다.
여기 방정식입니다:
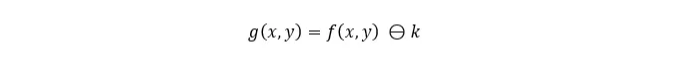
여기에 Python 구현이 있습니다:
#침식
fig, axes = plt.subplots(ncols=4, nrows=1, sharex=True, sharey=True, figsize=(12, 5))
image = im
thresh = threshold_otsu(image)
binary = image > thresh
eroded = ndimage.binary_erosion(binary, structure=np.ones((3,3)))
eroded1 = ndimage.binary_erosion(binary, structure=np.ones((5,5)))
eroded2 = ndimage.binary_erosion(binary, structure=np.ones((9,9)))
아래의 표를 마크다운 형식으로 바꿔보세요.

주의할 점은 작은 물체가 사라지는 것과, 관심 대상물체에 구멍이 형성되는 것입니다.
침식과 팽창의 조합으로 우리는 개방, 폐쇄, 경계 감지와 같은 복합 연산을 유도합니다.
폐쇄와 개방
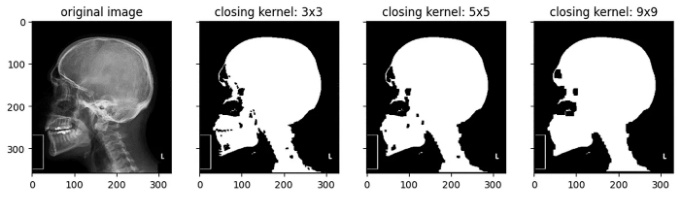
보통 클로징은 구멍을 메우는 연산입니다. 팽창에 이어 침식이 이루어지면 얻을 수 있습니다. 이미지 내부의 구멍은 보통 이 작업 이후에 닫힙니다. 팽창을 사용하여 객체의 크기 (그리고 잡음의 크기)를 키우고 출력 객체는 입력 크기와 같습니다. 따라서 클로징이 이 문제를 해결합니다. 다음 작업을 위한 커널의 크기도 동일합니다. 클로징 연산은 항등성을 갖고 있어 한 번만 사용할 수 있습니다. 그렇지 않으면 이미지 전체를 축소시키는 것만 일어나서 뚜렷한 효과가 없습니다 (경계 문제). 아래 방정식을 볼 수 있습니다:
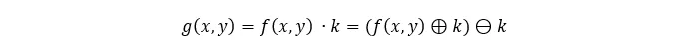
여기서 커널의 크기를 다르게 사용하는 경우 무슨 일이 일어나는지 주목해 보세요:
closed = ndimage.binary_closing(binary, structure=np.ones((3,3)))
closed1 = ndimage.binary_closing(binary, structure=np.ones((5,5)))
closed2 = ndimage.binary_closing(binary, structure=np.ones((9,9)))
Opening is generally used to avoid fractioning bigger objects when removing the noise. In this case, we use first erosion and then dilation. The output image presents an object with the original size but the noise is removed. Another idempotent transformation and the equation is:
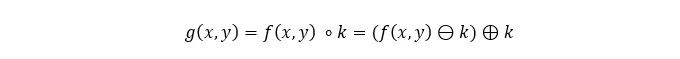
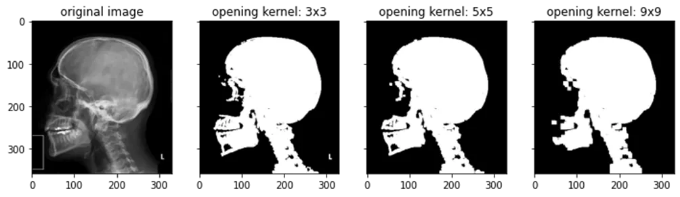
Let’s also test the opening operation to see what is happening:
opened = ndimage.binary_opening(binary, structure=np.ones((3,3)))
opened1 = ndimage.binary_opening(binary, structure=np.ones((5,5)))
opened2 = ndimage.binary_opening(binary, structure=np.ones((9,9)))
두 가지 과정을 결합할 수도 있지만, 커널은 서로 달라야 합니다 (opening에 사용되는 것과 closing에 사용되는 것이 서로 다른 커널이어야 함)
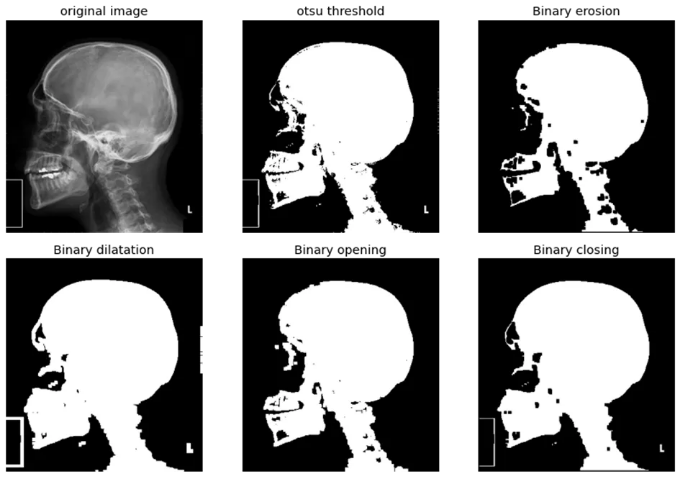
5x5 커널을 사용하여 모든 연산을 함께 확인해보겠습니다.
Boundary detection is an edge detection technique on binary images, where you subtract the eroded image, obtaining the boundary. The idea is that with eroding we are obtaining a smaller version of the object and if we subtract the image only the boundary will remain. In formula:
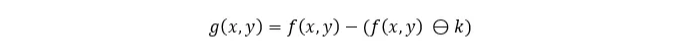
eroded = ndimage.binary_erosion(binary, structure=np.ones((3,3)))
boundary =binary ^ eroded
뺄셈이 아니라 두 개의 논리 마스크 (참/거짓)를 사용하기 때문에 논리 연산자 AND를 사용하는 것에 유의하세요. 그렇지 않으면 Numpy가 오류를 반환합니다. (하지만 원리는 같습니다)
약간의 실제 예시
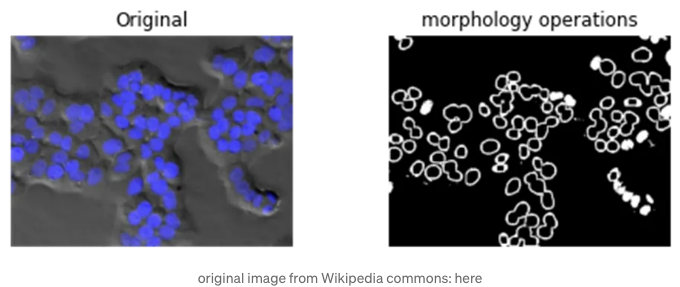
마이크로스코프 이미지에서 핵 윤곽선을 선택하여 분석을 수행하려면 몇 가지 조작만으로 가능합니다:
# 핵을 선택하려고 합니다.
# 따라서, 파란색 부분만 선택합니다.
im = a[:,:,2]
image = im
thresh = threshold_otsu(image)
binary = image > thresh
eroded = ndimage.binary_erosion(binary, structure=np.ones((7,7)))
opening = ndimage.binary_opening(eroded, structure=np.ones((11,11)))
boundary = binary ^ opening
보너스 예제: 자동차 이미지의 번호판을 읽고 싶다면, 복잡한 딥 러닝 모델 대신 간단한 전처리 단계로 시작할 수 있습니다. 하얀색과 검은색 모자(흰색은 회색 이미지에서 개방 이미지를 뺀 것이고 검은색은 회색 입력 이미지에서 닫힘을 뺀 것)와 같은 몇 가지 간단한 연산을 사용할 수 있습니다. 여기서 우리는 번호판이 가로보다 세로가 길기 때문에 사각형 커널을 사용했습니다. 그리고 임의의 크기의 커널을 사용할 수 있습니다. 몇 가지 간단한 작업만으로도 결과가 꽤 좋아집니다.
image = im
thresh = threshold_otsu(image)
binary = image > thresh
opening = ndimage.binary_opening(binary, structure=np.ones((13,5)))
closing = ndimage.binary_closing(binary, structure=np.ones((13,5)))
black_hat = im - closing
white_hat = im - opening

마무리

우리는 간단한 연산으로 다양한 결과를 얻을 수 있는 형태학적 연산이 얼마나 강력한지 보았습니다. 각 연산에는 그만의 반대가 있다는 것을 주목할 가치가 있으며, 이들을 결합하여 더 정교한 작업을 수행할 수 있습니다.
합성에서는 침식 기법을 사용하여 물체를 연결하는 작은 링크를 제거하거나 작은 잡음 물체를 제거하고 바이너리 이미지에서 경계를 감지할 수 있습니다. 반면 팽창은 이미지의 부분을 연결하는 데 유용합니다. 열림은 물체를 파괴하지 않고 작은 물체를 제거할 수 있게 하며, 폐쇄는 물체 크기를 늘리지 않으면서 구멍을 메울 수 있습니다. 그리고 이러한 작업을 필요에 맞게 반복 및 조합할 수도 있습니다. 간단한 작업에 대해 나쁘지 않죠?
이전 글은 여기서 확인할 수 있습니다. 여기에서는 핵심 코드만을 보여줬지만, 사용된 모든 코드는 여기에 있습니다.
어떻게 생각하세요? 이러한 작업을 시도해 보셨나요? 댓글로 알려주세요.
흥미로우셨다면:
제 다른 글을 찾아보실 수 있고, LinkedIn에서 연락이나 소통할 수도 있습니다. 매주 업데이트되는 머신 러닝 및 인공 지능 뉴스가 포함된 이 저장소를 확인해보세요. 협업 및 프로젝트에 대해 열려 있으며 LinkedIn에서 저에게 연락할 수 있습니다.
제 GitHub 저장소 링크는 다음과 같습니다. 거기에는 머신 러닝, 인공 지능 등과 관련된 코드와 다양한 자료를 모아두고 있습니다.
또는 최근 글 중 하나에 관심이 있을 수도 있습니다:
추가 자료
- 형태학 연산에 대해: 일반적으로 (여기, 여기, 여기) 및 OpenCV로 (여기, 여기, 여기)
- 화이트와 블랙 햇에 관해: 여기
평문으로 이해하기 🚀
In Plain English 커뮤니티의 일원이 되어 주셔서 감사합니다! 계속 진행하기 전에:
- 작가를 박수 치고 팔로우해 주세요 👏
- 팔로우: X | LinkedIn | YouTube | Discord | 뉴스레터
- 다른 플랫폼 방문: Stackademic | CoFeed | Venture
- PlainEnglish.io에서 더 많은 콘텐츠 확인하기