안녕하세요!

요즘에는 생성 AI와 거대한 신경망에 많은 관심이 집중되어 있지만, 예전에 시험해본 기계 학습 알고리즘을 간과하기 쉽습니다 (사실 그렇게 오래된 것은 아닌데요...). 대부분의 비즈니스 상황에 대해 단순한 기계 학습 솔루션이 복잡한 AI 구현보다 더 나아질 수 있다고 주장할 정도로 나는 생각해냅니다. 기계 학습 알고리즘은 극도로 확장 가능하며, 모델 복잡성이 낮아서 (내 의견에 따르면) 대부분의 시나리오에서 우수하다고 생각합니다. 그리고 또한, 그런 기계 학습 솔루션의 성능을 추적하는 것이 훨씬 더 쉬웠습니다.

본문에서는 클래식한 ML 문제에 클래식한 ML 솔루션을 사용할 것입니다. 구체적으로 말하자면, Random Forest 분류기를 사용하여 데이터 집합 내에서 특성의 중요성을 식별하는 방법을 (몇 줄의 코드만으로) 보여드리겠습니다. 이 기술의 효과를 시연한 후에는, 이 방법이 어떻게 작동하는지 자세히 살펴보기 위해 Decision Tree와 Random Forest를 처음부터 만들어가면서 모델을 벤치마킹할 것입니다.

저는 ML 프로젝트의 초기 단계를 전문적인 분위기에서 특히 중요하게 생각합니다. 이 프로젝트가 이길만한 가능성이 스테이크홀더들(계산서를 내는 사람들)로부터 승인받은 후에는, 그들은 투자에 대한 수읽성을 보고하길 원하게 될 것입니다. 이 가능성 논의의 일환으로 데이터의 상황에 대해 논의해야 할 것들이 있습니다: 충분한 데이터가 있는지, 데이터의 품질은 어떤가 등등. 몇 가지 초기 분석을 진행한 후에만 데이터의 분포 및 품질에 대한 일부 답을 할 수 있습니다. 여기서 제가 보여주는 기술은 초기 가능성 평가를 완료했다고 가정하고 다음 단계로 진행할 준비가 되었다고 가정합니다. 이 시점에서 스스로 물어봐야 할 주요 질문은: 모델 성능을 유지하면서 얼마나 많은 특성을 제거할 수 있을까요. 모델의 특성(차원)을 줄이는 것에는 많은 이점이 있습니다. 이 중에는 다음과 같은 것들이 포함되어 있지만 이에 한정되지 않습니다:

모델 복잡성 감소
학습 속도 향상
다중공선성 감소 (상관된 피처들)
잡음 감소
모델 성능 향상

랜덤 포레스트 기술을 사용하면 각 피처가 우리의 타겟을 설명하는 데 얼마나 중요한지 명확히 보여주는 그래프가 남습니다(타이타닉 탑승객이 죽었는지 여부… 네, 타이타닉 데이터셋을 사용 중이죠!). 또한 데이터에 적합한 초기 프로토 타입 모델을 보유하게 될 것이며, 추가적인 예측에 활용할 수 있습니다. 이것이 프로토타입에 불과하더라도, 나중에 진행할 실험의 기준이 되며 이 프로젝트가 여러분의 시간과 이해관계자들의 돈을 투자할 가치가 있다는 증거가 될 것입니다! 프로젝트 초기 단계에서 동력을 얻는 훌륭한 방법입니다.

반면에, 이 기술은 또한 여러분의 모델이 피처와 타겟 간의 관계를 더 잘 학습하기 위해 새로운 데이터포인트/피처를 만들거나 외부 소스에서 가져오는 데 노력할 필요가 있다는 것을 보여주는 데 도움이 될 수도 있습니다.

시작해봅시다

Random Forest 구현

의사결정 트리와 이들의 앙상블 버전인 Random Forests는 일반적으로 피처의 사전 처리(일부 인코딩만 필요)를 요구하지 않습니다. 의사결정 트리는 특정 기준에 따라 데이터를 가장 잘 분리하는 피처를 선택합니다. 이 기준을 'Gini 불순도'라고 합니다. 나중 섹션에서 의사결정 트리를 처음부터 만들 때 이에 대해 다룰 것입니다. 또한 의사결정 트리는 피처의 분포나 그들 간의 관계에 대해 가정하지 않습니다. 의사결정 트리는 임계값을 기준으로 피처 공간을 분할할 수 있어 데이터의 분포에 견고합니다. 의사결정 트리는 이상치에도 견고합니다. 나중에 보겠지만, 이들은 각 노드에서 이진 결정에 따라 데이터를 분할합니다. 이상치는 특정 노드에서 분할 임계값에 영향을 줄 수 있지만 개별 트리의 전체 성능에는 큰 영향을 미치지 않을 것입니다. '배깅'이라는 기법을 사용하여 여러 개의 Decision Trees의 평균 예측을 사용하여 Random Forest를 생성함으로써 성능을 향상시킬 수 있는 방법을 알아보겠습니다.

사전 처리와 피처 인코딩을 적용해야 하는 유일한 수정 사항입니다. 필요에 따라 내 코드를 적절히 조정하십시오.

우리는 Kaggle로부터 데이터셋을 가져와서 시작할 것입니다. Kaggle 데이터셋을 가져올 때, 로그인 자격 증명이 컴퓨터의 이 위치에 저장되어 있는지 확인해야 합니다:

~/.kaggle/kaggle.json

kaggle.json 파일에는 API 키가 포함되어 있습니다. 처음부터 시작하는 경우에는 Kaggle에 등록하고 계정 설정에 접근하여 API 헤더로 이동한 다음 '새 토큰 생성'을 클릭하면 됩니다. 이렇게 하면 kaggle.json 파일이 다운로드 폴더에 저장됩니다. 올바른 위치로 이동하려면 CLI(저는 제 맥의 터미널을 사용하고 있습니다)를 열고 다음 명령을 입력하십시오:

mv ~/Downloads/kaggle.json ~/.kaggle/

이 파일이 올바른 위치로 이동되었는지 확인할 수 있습니다. 입력하여 확인할 수 있습니다:

ls ~/.kaggle/

kaggle.json 파일이 보여야 합니다.

이제 API 자격 증명이 준비되었으니 필요한 모든 라이브러리를 가져와봅시다. 모듈을 찾을 수 없다는 오류가 발생하면 해당 라이브러리를 pip로 설치하면 됩니다. 문제가 발생하면 빠른 구글 검색으로 문제 해결이 가능합니다.

import pandas as pd
import numpy as np
np.set_printoptions(linewidth=130)
from pathlib import Path
import zipfile,kaggle
from numpy import random
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import mean_absolute_error

다음으로 데이터를 가져오고 훈련/테스트 데이터를 할당할 것입니다.

path = Path('titanic')
kaggle.api.competition_download_cli(str(path))
zipfile.ZipFile(f'{path}.zip').extractall(path)

df = pd.read_csv(path/'train.csv')
tst_df = pd.read_csv(path/'test.csv')
modes = df.mode().iloc[0]

이제 약간의 전처리를 다룰 것입니다. 다시 한 번, 이 코드를 개인적인 요구에 맞게 조정해주세요. 널 값에 값을 채우고, 요금을 로그 요금으로 변환합니다 (이는 주로 개인 취향에 따른 것이며, 앞서 설명했듯이, 의사 결정 트리는 이상값 및 데이터 분포에 대해 견고합니다). 또한, Embarked 및 Sex 열의 범주형 변환을 설정합니다.

def process_data(df):
    df['Fare'] = df.Fare.fillna(0)
    df.fillna(modes, inplace=True)
    df['LogFare'] = np.log1p(df['Fare'])
    df['Embarked'] = pd.Categorical(df.Embarked)
    df['Sex'] = pd.Categorical(df.Sex)

process_data(df)
process_data(tst_df)

그럼 범주형, 연속 및 종속 변수를 식별할 것입니다 :

cats = ["Sex", "Embarked"];
conts = ["Age", "SibSp", "Parch", "LogFare", "Pclass"];
dep = "Survived";

그 다음, 데이터를 분할한 다음 범주형 변환을 적용해야 합니다:

random.seed(42)
trn_df,val_df = train_test_split(df, test_size=0.25)
trn_df[cats] = trn_df[cats].apply(lambda x: x.cat.codes)
val_df[cats] = val_df[cats].apply(lambda x: x.cat.codes)

그럼 독립 변수(x)와 종속 변수(y)를 할당해보겠습니다:

def xs_y(df):
    xs = df[cats+conts].copy()
    return xs, df[dep] if dep in df else None

trn_xs, trn_y = xs_y(trn_df)
val_xs, val_y = xs_y(val_df)

이제 sklearn의 RandomForestClassifier() 클래스를 사용하여 랜덤 포레스트를 맞추기 준비가 되었습니다. 이 클래스의 좋은 점은 featureimportances라는 밑바닥 메소드가 있어서 특정 feature가 승객의 생존율에 미치는 영향을 식별하고 플롯할 수 있다는 것입니다. 또한 mean_absolute_error를 통해 모델의 성능을 평가할 수 있습니다:

rf = RandomForestClassifier(100, min_samples_leaf=5)
rf.fit(trn_xs, trn_y)
mean_absolute_error(val_y, rf.predict(val_xs))
# 0.18834080717488788

우리 발견물을 그래프로 표현해 보겠습니다:

pd.DataFrame(dict((cols = trn_xs.columns), (imp = rf.feature_importances_))).plot("cols", "imp", "barh");

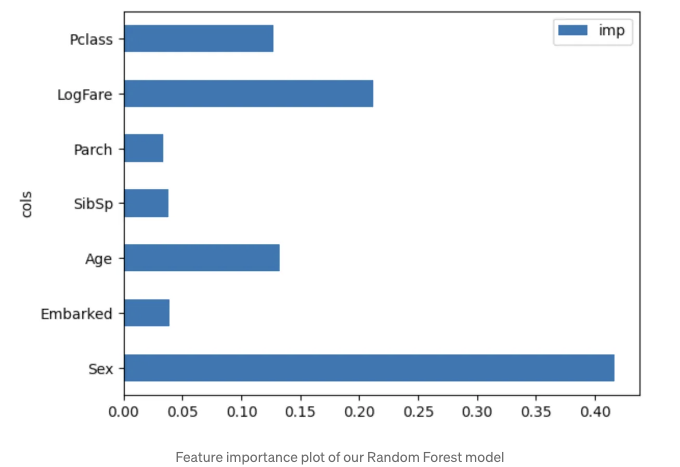
여기서요. 생존 예측에서 성별이 가장 중요한 요소임을 알 수 있습니다. 이 단계에서는 다른 알고리즘을 실험하면서 현재 특성을 유지하거나, 랜덤 포레스트 모델을 성능 기준으로 활용할 수 있습니다. 또한, 모델의 예측 성능이 부족하다면, 더 많은 특성 엔지니어링을 수행할 수도 있습니다. 이 방법은 극히 작은 데이터셋으로만 실험했지만, 매우 효율적으로 확장할 수 있는 방법입니다. 1000개 이상의 특성이 있는 데이터셋이 있다고 상상해보세요. 이 방법을 사용하면 빠르게 상위 특성을 추출하여 프로젝트를 어떻게 가장 잘 진행할지 계획을 세울 수 있습니다.

자세히 살펴보기…

이제 우리는 데이터셋 내에서 특성 중요도를 보여주는 랜덤 포레스트를 구현하는 방법을 갖게 되었으니, 어떻게 그 과정을 거쳤는지 알아보겠습니다. 수동으로 결정 트리를 만들고 여기서부터 진행해보겠습니다.

승객의 생존 여부를 이해하는 데 데이터셋에서 성별이 가장 중요한 특성임을 알고 있습니다. 특정 이진 분할의 불순도를 측정하는 몇 가지 스코어링 함수를 만들어서 이를 수동으로 테스트할 수 있습니다. 불순도는 특정 특성(예: 성별)에 대한 분할이 각 그룹 내의 행이 서로 유사하거나 다른 정도를 나타냅니다. 목표는 특성에 대한 분할을 만들어 이 불순도를 줄이는 것이며, 이를 통해 우리의 특성과 목표 간의 관계를 가장 잘 설명하는 특성에 대한 분할을 생성하는 것입니다. 이전의 랜덤 포레스트 예제에서, 개별 결정 트리는 "성별" 열을 분할하도록 선택한 이유는 그 열이 (생존 및 비생존) 클래스 간에 가장 작은 혼합을 만들어줘서 결과를 예측하는 데 불확실성(불순도)을 줄이기 때문입니다. 이진 분할은 의사 결정 트리의 첫 번째 구성 요소이며, 여기서 각 특성마다 이진 분할이 이뤄집니다.

그룹 내 행의 유사성을 측정하기 위해 종속 변수의 표준 편차를 취할 것입니다. 표준 편차가 높을수록 행들 사이에 차이가 더 크다는 뜻입니다. 그런 다음 이 값을 행 수로 곱할 것입니다. 왜냐하면 값들이 더 큰 그룹이 더 작은 그룹보다 더 큰 영향을 미치기 때문입니다.

def side_score(side, y):
    tot = side.sum()
    if tot <= 1:
        return 0
    return y[side].std() * tot

이제 좌측과 우측의 점수를 더하여 분할에 대한 점수를 계산할 수 있습니다:

def score(col, y, split):
    lhs = col <= split
    return (side_score(lhs, y) + side_score(~lhs, y)) / len(y)

0.5로 임계값을 설정하여 성별 열의 불순도 점수를 확인할 수 있습니다. 데이터 내에서 여성 승객은 0으로 표현되고, 남성은 1로 표현됩니다.

score(trn_xs["Sex"], trn_y, 0.5)
# 0.40787530982063946

다른 요소들에 대해서는 임계값이 명확하지 않습니다. 다른 범주형 또는 상수 변수에 대한 실험을 설정하여 데이터의 불순도에 어떤 영향을 미치는지 확인할 수 있습니다. 각 분할에서 불순도를 줄이고 데이터의 순도를 높이기를 원합니다:

def iscore(nm, split):
    col = trn_xs[nm]
    return score(col, trn_y, split)

from ipywidgets import interact
interact(nm=conts, split=15.5)(iscore);

이제 슬라이더를 사용해보세요. 연속 변수에만 적용했지만 범주형 변수에도 테스트할 수 있습니다. 모든 기능에 대해 이 작업을 수행하면 다소 시간이 소요됩니다. 열의 최적 분할점을 찾을 수 있는 함수를 작성해 봅시다. 해당 필드의 모든 가능한 분할점(해당 필드의 고유한 값) 목록을 만들고 score()가 가장 낮은 지점을 찾아야 합니다:

def min_col(df, nm):
    col,y = df[nm],df[dep]
    unq = col.dropna().unique()
    scores = np.array([score(col, y, o) for o in unq if not np.isnan(o)])
    idx = scores.argmin()
    return unq[idx],scores[idx]

min_col(trn_df, "나이")
# (6.0, 0.478316717508991)

좋아요. 우리의 훈련 세트의 "나이" 열에서 최적 분할이 6인 것을 찾았고, 불순도 점수는 0.478입니다.

모든 열에 대해 이 아이디어를 구현해 봅시다:

cols = cats + conts
{o: min_col(trn_df, o) for o in cols}
# {'성별': (0, 0.40787530982063946),
# '승선항': (0, 0.47883342573147836),
# '나이': (6.0, 0.478316717508991),
# '형제_배우자': (4, 0.4783740258817434),
# '부모_자녀': (0, 0.4805296527841601),
# '로그요금': (2.4390808375825834, 0.4620823937736597),
# '선실등급': (2, 0.46048261885806596)}

그래서, Sex`=0이 최적의 분할이라고 하는 것은 우리의 불순도 점수가 가장 낮을 때입니다. 이 결과들이 초기 랜덤 포레스트 예제와 정확히 일치하지는 않지만 (데이터의 작은 하위 집합만 사용하고 앙상블 방법을 사용하지 않기 때문에 이해하기 쉽다), 여전히 올바른 방향으로 나아가고 있다는 것을 보여줍니다. 본질적으로 OneR 분류기의 기본 버전을 재현한 것입니다.

의사 결정 트리 탐색

여기서부터 진행하려면 Sex 열을 초기 최적 분할로 선택하는 것이 중요합니다. 다음 단계로 수동으로 이동하여 데이터를 남성/여성으로 분할한 후 각 그룹에 대한 다음 최적 분할이 무엇인지 결정합니다. 이것이 어디에 향하고 있는지 볼 수 있습니다. 우리는 다음 단계로 이동하여 의사 결정 트리의 구성 요소를 모아가고 있습니다. 그러기 위해서, 가능한 분할 목록에서 Sex를 제거해야 합니다. 그런 다음 데이터를 남성 또는 여성으로 분할하고 각 그룹의 최적 분할을 찾아야 합니다 (불순도 점수가 가장 낮은 분할). 시작해 봅시다.

Sex 열을 제거하고 데이터를 분할합니다. 이것은 사실상 의사 결정 트리 내에서 첫 번째 이진 분할입니다.

cols.remove("Sex");
ismale = trn_df.Sex == 1;
males, (females = trn_df[ismale]), trn_df[~ismale];

이제 우리는 남성들에 대한 최적의 분할을 찾습니다:

{o:min_col(males, o) for o in cols}
# {'Embarked': (0, 0.3875581870410906),
# 'Age': (6.0, 0.3739828371010595),
# 'SibSp': (4, 0.3875864227586273),
# 'Parch': (0, 0.3874704821461959),
# 'LogFare': (2.803360380906535, 0.3804856231758151),
# 'Pclass': (1, 0.38155442004360934)}

그리고 여성들에 대한 최적의 분할:

{cols의 o에 대해 females 최소 열계수(females, o) for o in cols}
# {'Embarked': (0, 0.4295252982857327),
# 'Age': (50.0, 0.4225927658431649),
# 'SibSp': (4, 0.42319212059713535),
# 'Parch': (3, 0.4193314500446158),
# 'LogFare': (4.256321678298823, 0.41350598332911376),
# 'Pclass': (2, 0.3335388911567601)}

남성의 경우, 다음 최적의 이진 분할은 Age=6이고, 여성의 경우는 Pclass=2입니다. 여기서 불순도 점수가 가장 낮았습니다.

여러분은 손으로 첫 번째 의사 결정 트리를 만들었습니다. 우리는 지금 생성한 네 개의 하위 그룹마다 추가적인 규칙을 만들어 이 과정을 반복할 수 있습니다. 그러나 우리가 바퀴를 재발명할 필요는 없습니다. 우리 대신에 많은 오픈 소스 라이브러리가 중요한 작업을 대신 해줍니다. 동일한 프로세스를 반복하되, 기존 라이브러리를 사용하고 결과 의사 결정 트리를 출력하여 우리의 발견을 비교해 보겠습니다:

from sklearn.tree import DecisionTreeClassifier, plot_tree
import matplotlib.pyplot as plt

model = DecisionTreeClassifier(max_leaf_nodes=4).fit(trn_xs, trn_y)
plt.figure(figsize=(20, 10))
plot_tree(model, feature_names=trn_xs.columns, filled=True, max_depth=3, rounded=True, precision=2)
plt.show()

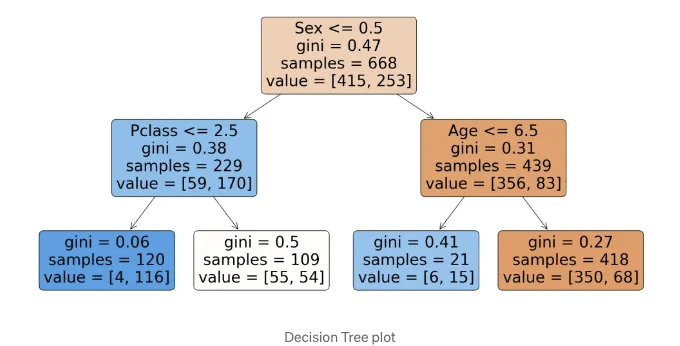
와우, 수동 분리 결과와 동일한 결과를 얻었네요. 이 모델의 성능을 측정해 봅시다:

mean_absolute_error(val_y, model.predict(val_xs))
# 0.2242152466367713

예상대로, 이 모델은 처음에 생성한 랜덤 포레스트 앙상블 모델보다 성능이 낮습니다. 다이어그램의 각 노드는 특정 규칙 집합과 일치하는 행/샘플이 몇 개인지 및 생존 또는 사망한 승객이 몇 명인지를 보여줍니다. Gini 점수는 이전에 만든 점수 기능과 매우 유사합니다. 다음과 같이 정의됩니다:

def gini(cond):
    act = df.loc[cond, dep]
    return 1 - act.mean()**2 - (1-act).mean()**2

이 함수는 조건에 따라 지니 불순도를 계산합니다. 여기서, 먼저 사용자가 선택한 두 행이 각각 "Survived" 결과가 같을 확률을 계산합니다. 그룹이 모두 같은 경우, 확률은 1.0입니다. 모두 다른 경우에는 0.0의 결과가 나옵니다.

더 큰 의사 결정 트리…

더 큰 의사 결정 트리를 만들어 성능에 어떤 영향을 미치는지 살펴봅시다:

model = DecisionTreeClassifier(min_samples_leaf=50).fit(trn_xs, trn_y)
plt.figure(figsize=(20, 10))
plot_tree(model, feature_names=trn_xs.columns, filled=True, rounded=True, precision=2)
plt.show()

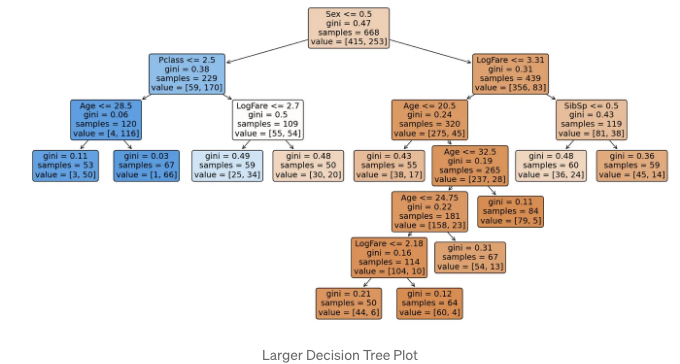
이제 큰 모델의 성능을 측정해 보겠습니다:

mean_absolute_error(val_y, model.predict(val_xs))
# 0.18385650224215247

이 모델은 초기 모델보다 우수한 성능을 보입니다. 그러나 데이터셋이 매우 작기 때문에 이 점을 고려해야 할 것 같아요.

손수 랜덤 포레스트…

마지막으로, 직접 랜덤 포레스트 분류기를 만들어보겠습니다. 우리는 sklearn의 학습 방법을 사용하여 많은 개별 의사 결정 트리를 만들 것입니다. 그리고 각 개별 의사 결정 트리의 출력의 평균을 취할 것입니다. 여기서 아이디어는 상관 관계가 없는 모델의 예측을 평균 내어 예측 오차를 줄인다는 점입니다. 여기서 중요한 것은 '상관 관계가 없는'입니다. 우리의 각 의사 결정 트리가 데이터의 고유한 하위 집합에서 트레이닝을 수행하도록 보장해야 합니다. 따라서 각 의사 결정 트리의 성능은 개별적으로 평균보다 조금 더 나을 것입니다. 각각은 너무 높게 또는 너무 낮게 예측할 것입니다. 여러 개의 개별, 편향되지 않은 상관 관계가 없는 의사 결정 트리의 예측을 평균 내어 정확하게 참 값을 얻을 수 있습니다. 이것은 상관 관계가 없는 무작위 오류의 평균은 0이기 때문입니다. 상당히 멋지죠. 이 기술은 배깅이라고 알려져 있습니다. 이를 코드로 구현해봅시다.

먼저, 데이터의 새로운 무작위 하위 집합에 대한 의사 결정 트리 생성을 다룹니다:

def get_tree(prop=0.75):
    n = len(trn_y)
    idxs = random.choice(n, int(n*prop))
    return DecisionTreeClassifier(min_samples_leaf=5).fit(trn_xs.iloc[idxs], trn_y.iloc[idxs])

이제 원하는 만큼의 트리를 생성합니다:

trees = [get_tree() for t in range(100)]

이제 모든 트리의 평균 예측값을 얻습니다:

all_probs = [t.predict(val_xs) for t in trees]
avg_probs = np.stack(all_probs).mean(0)

mean_absolute_error(val_y, avg_probs)
# 0.22524663677130047

이 방법론은 이 글 초반에서 설명한 랜덤 포레스트 분류기에서 사용하는 방식과 거의 동일합니다. 유일한 차이는 sklearn에서 각 분할마다 무작위로 열의 부분 집합을 선택한다는 것뿐입니다.

결론

요령이다. 데이터셋 내에서 가장 중요한 기능을 이해하는 데 도움이 되는 기본 요소를 다루었습니다. 이 방법론을 적용하여 데이터 과학 프로젝트에서 신속히 진전할 수 있기를 바라겠습니다. 앞서 말했듯이, 이 글에 소개된 각 모델의 성능 기준은 우리의 데이터셋이 매우 작았기 때문에 준중요하게 여겨야 합니다. 그럼에도 불구하고, 이 방법은 놀랍도록 잘 확장되며 설명 가능한 기준을 설정하는 좋은 방법입니다.

언제든지 궁금한 점이 있거나 기사에서 언급된 내용에 대해 논의를 원하시면 언제든지 말씀해 주세요.

건배하세요!

모든 이미지는 명시되지 않는 한 작성자에게 속합니다.

랜덤 포레스트로 PCA와 특징 중요도 해제하는 방법

Random Forest 구현

자세히 살펴보기…

의사 결정 트리 탐색

더 큰 의사 결정 트리…

손수 랜덤 포레스트…

결론