
신경망의 매혹적인 세계에서 손실 함수는 훈련 과정을 정확한 예측으로 이끄는 안내 나침반 같은 역할을 합니다. 이러한 함수들을 숙달하는 것은 딥러닝에 진지하게 임하는 사람들에게 중요합니다. 왜냐하면 손실 함수를 선택하는 것은 모델의 성능에 상당한 영향을 미칠 수 있기 때문입니다. 신진 데이터 과학자든 경험 많은 기계 학습 엔지니어든, 이 블로그는 다양한 손실 함수를 해독하고 그 목적을 설명하며, 처음부터 구현하는 방법을 보여줍니다.
자, 이러한 수학적 도구가 어떻게 신경망 훈련을 변화시킬 수 있는지 알아봅시다!
그래서, 우리 마음에 떠오르는 첫 번째 질문은 '손실 함수란 무엇인가요?'입니다.
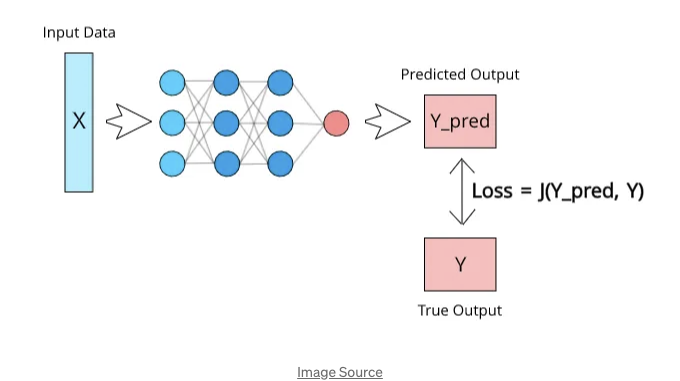
핵심적으로, 손실 함수(J로 표시됨)는 두 개의 매개변수를 입력으로 받는 수학 함수입니다:
- 예측된 출력
- 실제 출력
이 함수는 모델의 예측 값과 모델이 생성해야 하는 실제 값과 비교하여 모델이 얼마나 잘 작동하는지를 평가하기 위해 사용됩니다. 예측 값이 실제 값과 크게 다를 경우 손실 값은 크게 나타납니다. 반면, 낮은 손실 값은 두 값이 거의 유사할 때 발생합니다. 따라서 효율적인 손실 함수를 사용하여 모델을 올바르게 훈련시키는 것이 중요합니다.
높은 손실 값은 모델의 예측이 부정확하다는 것을 시사하며, 네트워크를 크게 재조정해야 한다는 것을 의미합니다. 반면에 낮은 손실 값은 모델이 효과적으로 작동하고 있으며, 가중치를 매우 약간만 조정해야 한다는 것을 나타냅니다.
이러한 시나리오는 새로운 요리법을 만드는 것과 유사합니다. 요리물이 실패하면 "손실"이 높아지고, 요리사는 다음에 요리물을 개선하기 위해 재료나 조리 방법에 상당한 변화를 해야 합니다. 그러나 요리물이 잘 나오면 이미 효과적인 레시피와 기술이기 때문에 필요한 경우에는 작은 조정만 필요합니다. 이 조정은 향후 블로그에서 논의할 하이퍼파라미터를 조정함으로써 수행할 수 있습니다. 이제 손실 함수가 무엇인지 이해했으므로, 다음으로 궁금한 것은 어떤 종류의 손실 함수가 있고 이를 어떻게 구현하는지에 대한 것입니다.
신경망에서의 손실 함수 유형
회귀 손실 함수
- 평균 제곱 오차 (MSE)
MSE는 회귀 문제에 사용되는 가장 인기 있는 손실 함수 중 하나입니다. 이는 예측 값과 실제 값 사이의 오차의 제곱의 평균을 측정합니다. MSE는 이상치에 민감합니다.
사용 사례: MSE는 주택 가격이나 온도와 같은 연속적인 값을 예측하는 회귀 문제에서 흔히 사용됩니다.
수학적 공식:
아래는 Markdown 형식으로 표시된 내용입니다.
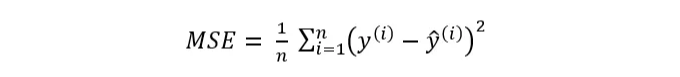
where,

코드 구현:
def mean_squared_error(y_true, y_predicted):
total_error = 0
for yt, yp in zip(y_true, y_predicted):
total_error += (yt-yp)**2
mse = total_error/len(y_true)
return mse
- Mean Absolute Error (MAE)
MAE는 예측 값과 실제 값 사이의 절대 오차의 평균을 측정합니다. MSE보다 이상치에 민감하지 않습니다.
사용 사례: MAE는 중앙값 주택 가격을 예측하는 경우와 같이, 이상치에 민감하지 않은 손실 함수를 원할 때 사용됩니다.
수학 공식:
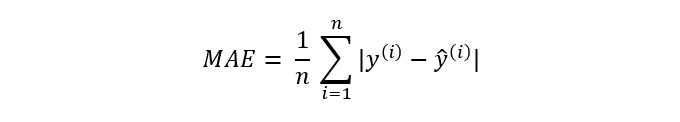
코드 구현:
def mean_abs_error(y_predicted, y_true):
total_error = 0
for yp, yt in zip(y_predicted, y_true):
total_error += abs(yp - yt)
mae = total_error/len(y_predicted)
return mae
- 휴버 손실
휴버 손실은 MSE와 MAE의 우수한 특성을 결합하여, MSE보다 이상치에 민감하지 않고 MAE보다 원점 주변에서 부드럽습니다.
사용 사례: 휴버 손실은 이상치의 영향을 줄이고 손실 함수를 미분 가능하게 유지하고자 하는 견고한 회귀 문제에서 자주 사용됩니다.
수학적 공식:
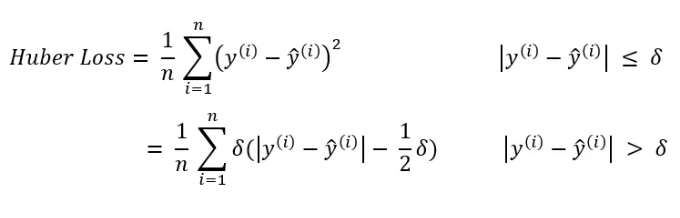
코드 구현:
def huber_loss(y_true, y_pred, delta=1.0):
n = len(y_true)
loss = 0
for i in range(n):
diff = y_true[i] - y_pred[i]
if abs(diff) <= delta:
loss += 0.5 * diff ** 2
else:
loss += delta * (abs(diff) - 0.5 * delta)
return loss / n
분류 손실 함수
- Binary Cross-Entropy 손실
Binary Cross-Entropy 손실은 이진 분류 작업에 사용됩니다. 출력이 0과 1 사이의 확률 값인 분류 모델의 성능을 측정합니다.
사용 사례: 스팸 감지나 사기 탐지와 같은 이진 분류 문제에 이 손실 함수가 이상적입니다.
수학적 공식:
이미지 태그를 Markdown 형식으로 변경하세요.
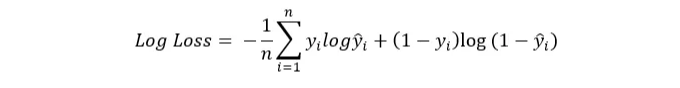
코드 구현:
import math
def binary_crossentropy(y_true, y_pred):
n = len(y_true)
loss = 0
for i in range(n):
loss += y_true[i] * math.log(y_pred[i]) + (1 - y_true[i]) * math.log(1 - y_pred[i])
return -loss / n
- 범주형 Cross-Entropy Loss
범주형 크로스 엔트로피 손실은 다중 클래스 분류 작업에 사용됩니다. 이는 여러 클래스에 대한 확률 분포인 분류 모델의 성능을 측정합니다.
활용 사례: 이 손실 함수는 숫자 인식(MNIST)이나 물체 검출과 같은 다중 클래스 분류 문제에 적합합니다.
수학적 공식:
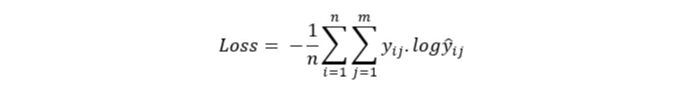
구현된 코드:
import math
def categorical_crossentropy(y_true, y_pred):
n = len(y_true)
c = len(y_true[0])
loss = 0
for i in range(n):
for j in range(c):
if y_true[i][j] == 1:
loss += y_true[i][j] * math.log(y_pred[i][j])
return -loss / n
- Sparse Categorical Cross-Entropy Loss
Sparse Categorical Cross-Entropy는 목표 레이블이 원-핫 인코딩된 벡터가 아닌 정수일 때 사용됩니다.
사용 사례: 이 손실 함수는 타겟 레이블이 one-hot 벡터가 아닌 정수 레이블 형태인 다중 클래스 분류 문제에서 사용됩니다.
수학적 공식:
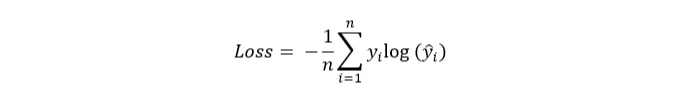
코드 구현:
def sparse_categorical_cross_entropy(y_true, y_pred):
n = len(y_true)
loss = 0
for i in range(n):
loss += y_true[i] * math.log(y_pred[i]))
return -loss / n
거기에는 몇 가지 더 특별한 손실 함수가 있어요:
- Kullback-Leibler Divergence
- Cosine Similarity Loss
- Dice Loss
- Quantile Loss
- Hinge Loss
이제 손실 함수에 대해 간결하고 명확하게 이해하셨기를 바랍니다. 다가오는 블로그에서는 특별한 손실 함수, 사용 사례 및 구현에 대해 논의할 예정이에요. 컴퓨터 비전과 딥 러닝에 관한 더 많은 기사를 위해 블로그를 팔로우해 주세요. 궁금한 사항이 있거나 특정 부분에 대한 추가 정보가 필요하면 언제든지 의견을 남겨주세요!
마크다운 형식으로 표 태그를 변경하세요: Linkedin