
머신 러닝에서는 몇 가지 모델을 시도해 가장 성능이 좋은 것을 선택하고 몇 가지 설정을 조정하여 그나마 성공할 수 있을지도 모릅니다. 그러나 딥러닝은 그런 룰에 맞지 않습니다. 신경망을 실험해 본 적이 있다면, 성능이 꽤 불안정할 수 있다는 것을 눈치챌 수 있습니다. 어쩌면 로지스틱 회귀와 같이 간단한 모델이 멋진 200층 심층 신경망을 이길 수도 있습니다.
이게 왜 그럴까요? 딥러닝은 우리가 가지고 있는 가장 고급 인공 지능 기술 중 하나이지만, 철저한 이해와 조심스러운 다룸이 필요합니다. 신경망을 세밀하게 조정하고, 내부 작동 방식을 파악하고, 그 사용법을 마스터하는 것이 중요합니다. 오늘은 이에 대해 자세히 살펴보겠습니다!
글을 읽기 전에 Jupyter Notebook을 여시는 것을 제안합니다. 오늘 다룰 모든 코드가 담겨 있으므로 함께 따라가는 데 도움이 될 것입니다:
인덱스
-
1: 소개
- 1.1: 기본 신경망의 발전
- 1.2: 복잡성으로의 길
-
2: 모델 복잡성 확장
- 2.1: 레이어 추가
-
3: 향상된 학습을 위한 최적화 기법
- 3.1: 학습률
- 3.2: 조기 중단 기법
- 3.3: 초기화 방법
- 3.4: 드롭아웃
- 3.5: 그래디언트 클리핑
-
4: 최적 레이어 수 결정하기
- 4.1: 레이어 깊이와 모델 성능
- 4.2: 적절한 깊이 선택을 위한 테스트 전략
-
5: Optuna를 활용한 자동 세부 조정
- 5.1: Optuna 소개
- 5.2: 신경망 최적화를 위한 Optuna 통합
- 5.3: 실제 적용
- 5.4: 장점과 결과
- 5.5: 제한 사항
-
6: 결론
- 6.1: 다음 단계
-
추가 자료
1: 소개
1.1: 기본 신경망의 발전
인공 지능에 대한 최근 탐구에서 우리는 기초부터 신경망을 구축했습니다. 이 기본 모델은 오늘날 인공 지능 기술의 핵심인 신경망의 세계를 열어 주었습니다. 우리는 입력, 은닉 및 출력 레이어와 활성화 함수가 어떻게 정보를 처리하고 예측하는 데 결합되는지 간단하게 다루었습니다. 그리고 나서 우리는 컴퓨터 비전 작업을 위해 숫자 데이터셋에서 훈련된 간단한 신경망으로 이론을 실제로 적용했습니다.
이제 이러한 기초 위에 계속해서 더 진보해 나갈 것입니다. 우리는 레이어를 추가하고, 초기화, 정규화 및 최적화에 대한 다양한 기술을 탐구함으로써 더 많은 복잡성을 도입할 것입니다. 물론, 이러한 수정이 우리의 신경망 성능에 어떻게 영향을 미치는지 확인하기 위해 코드를 테스트할 것입니다.
제가 이전 기사를 확인하지 않으셨다면, 우리가 처음부터 신경망을 만들어본 기사를 꼭 읽어보시기를 추천합니다. 이번에는 그 작업을 기반으로 계속해서 진행할 것이며, 이미 우리가 다룬 개념에 익숙하다고 가정할게요.
1.2: 복잡성으로의 길
신경망을 기본 구성에서 더 정교한 구조로 변환하는 것은 단순히 더 많은 층이나 노드를 추가하는 것만으로는 이루어지지 않습니다. 이것은 신경망의 구조와 그 데이터를 다루는 미묘한 차이를 체화하는 세심한 작업이 필요한 미묘한 춤이죠. 더 깊게 파고들수록, 우리의 목표는 신경망의 깊이를 풍부하게 함으로써 데이터의 복잡한 패턴과 연결을 더 잘 분별하는 데 있습니다.
하지만 복잡성을 높이는 것은 그리 수월한 일이 아닙니다. 우리가 도입할 때마다, 세련된 최적화 기술의 필요성이 커집니다. 이는 효과적인 학습뿐만 아니라 새로운 보이지 않는 데이터에 적응하기 위한 모델 능력에 필수적입니다. 이 안내서는 우리의 기반 신경망을 강화하는 과정을 안내해 드릴 것입니다. 우리는 신경망을 세밀하게 조정하는 정교한 전략에 대해 살펴볼 것이며, 학습 속도 조정, 조기 종료 도입, 그리고 SGD(확률적 경사 하강법)와 Adam과 같은 다양한 최적화 알고리즘을 활용하는 방법에 대해 살펴볼 것입니다.
우리는 초기화 방법으로 시작하는 중요성, 오버피팅을 피하는 데 드롭아웃 사용의 장점, 그리고 클리핑 및 정규화로 네트워크의 그래디언트를 체크하여 안정성을 유지하는 것이 모델의 안정성에 얼마나 중요한지에 대해 다룰 예정입니다. 또한 학습을 향상시키기 위한 레이어의 최적 개수를 찾는 도전과정 및 불필요한 복잡성으로 빠져들지 않도록 할 것입니다.
이전 게시물에서 함께 만든 Neural Network 및 Trainer 클래스를 아래에서 확인할 수 있습니다. 우리는 이를 조정하고 각 수정이 모델의 성능에 어떤 영향을 미치는지 실제로 살펴볼 것입니다:
class NeuralNetwork:
def __init__(self, input_size, hidden_size, output_size, loss_func='mse'):
self.input_size = input_size
self.hidden_size = hidden_size
self.output_size = output_size
self.loss_func = loss_func
# 가중치 및 편향 초기화
self.weights1 = np.random.randn(self.input_size, self.hidden_size)
self.bias1 = np.zeros((1, self.hidden_size))
self.weights2 = np.random.randn(self.hidden_size, self.output_size)
self.bias2 = np.zeros((1, self.output_size))
# 손실 추적
self.train_loss = []
self.test_loss = []
def __str__(self):
return f"Neural Network Layout:\n입력 레이어: {self.input_size} 뉴런\n은닉 레이어: {self.hidden_size} 뉴런\n출력 레이어: {self.output_size} 뉴런\n손실 함수: {self.loss_func}"
def forward(self, X):
# 순방향 전파 수행
self.z1 = np.dot(X, self.weights1) + self.bias1
self.a1 = self.sigmoid(self.z1)
self.z2 = np.dot(self.a1, self.weights2) + self.bias2
if self.loss_func == 'categorical_crossentropy':
self.a2 = self.softmax(self.z2)
else:
self.a2 = self.sigmoid(self.z2)
return self.a2
def backward(self, X, y, learning_rate):
# 역전파 수행
m = X.shape[0]
# 기울기 계산
if self.loss_func == 'mse':
self.dz2 = self.a2 - y
elif self.loss_func == 'log_loss':
self.dz2 = -(y/self.a2 - (1-y)/(1-self.a2))
elif self.loss_func == 'categorical_crossentropy':
self.dz2 = self.a2 - y
else:
raise ValueError('잘못된 손실 함수')
self.dw2 = (1 / m) * np.dot(self.a1.T, self.dz2)
self.db2 = (1 / m) * np.sum(self.dz2, axis=0, keepdims=True)
self.dz1 = np.dot(self.dz2, self.weights2.T) * self.sigmoid_derivative(self.a1)
self.dw1 = (1 / m) * np.dot(X.T, self.dz1)
self.db1 = (1 / m) * np.sum(self.dz1, axis=0, keepdims=True)
# 가중치 및 편향 업데이트
self.weights2 -= learning_rate * self.dw2
self.bias2 -= learning_rate * self.db2
self.weights1 -= learning_rate * self.dw1
self.bias1 -= learning_rate * self.db1
def sigmoid(self, x):
return 1 / (1 + np.exp(-x))
def sigmoid_derivative(self, x):
return x * (1 - x)
def softmax(self, x):
exps = np.exp(x - np.max(x, axis=1, keepdims=True))
return exps/np.sum(exps, axis=1, keepdims=True)
class Trainer:
def __init__(self, model, loss_func='mse'):
self.model = model
self.loss_func = loss_func
self.train_loss = []
self.val_loss = []
def calculate_loss(self, y_true, y_pred):
if self.loss_func == 'mse':
return np.mean((y_pred - y_true)**2)
elif self.loss_func == 'log_loss':
return -np.mean(y_true*np.log(y_pred) + (1-y_true)*np.log(1-y_pred))
elif self.loss_func == 'categorical_crossentropy':
return -np.mean(y_true*np.log(y_pred))
else:
raise ValueError('잘못된 손실 함수')
def train(self, X_train, y_train, X_test, y_test, epochs, learning_rate):
for _ in range(epochs):
self.model.forward(X_train)
self.model.backward(X_train, y_train, learning_rate)
train_loss = self.calculate_loss(y_train, self.model.a2)
self.train_loss.append(train_loss)
self.model.forward(X_test)
test_loss = self.calculate_loss(y_test, self.model.a2)
self.val_loss.append(val_loss)
2: 모델 복잡성 확대
신경망을 더 정교하게 개선하기 위해 깊이 파고들면서, 게임을 바꾸는 전략을 발견했습니다: 레벨을 더 쌓아 복잡성을 높이는 것입니다. 이 동작은 모델을 강화하는 것뿐만 아니라, 데이터의 미묘한 변화를 더 정교하게 이해하고 해석하는 능력을 키우는 것입니다.
2.1: 레이어 추가
증가된 네트워크 깊이의 근거 딥러닝의 핵심은 계층적 데이터 표현을 조합하는 능력에 있습니다. 더 많은 레이어를 추가함으로써, 우리는 신경망에 성장하는 복잡성의 패턴을 해체하고 이해하기 위한 도구를 제공하는 셈입니다. 간단한 형태와 질감을 인식하는 데서 시작해 데이터 속에서 더 복잡한 관계와 특징을 풀어가는 데로 발전하는 것으로 생각해보세요. 이러한 계층적 학습 접근법은 어느 정도 인간이 정보를 해석하는 방식과 유사하며, 기본적인 이해에서 복잡한 해석으로 진화합니다.
더 많은 레이어를 쌓으면 네트워크의 "학습 용량"이 증가하여 보다 넓은 범위의 데이터 관계를 매핑하고 소화하는 능력을 갖추게 됩니다. 이를 통해 더 복잡한 작업을 처리할 수 있습니다. 하지만 마구 레이어를 추가하는 것은 아니며, 모델의 지능에 의미 있는 기여를 하지 않고 무분별하게 레이어를 추가하면 학습 과정을 혼란시키는 것이 아니라 명료하게 해야 합니다.
NeuralNetwork 클래스를 더 많은 층을 통합하는 방법 안내
class NeuralNetwork:
def __init__(self, layers, loss_func='mse'):
self.layers = []
self.loss_func = loss_func
# 레이어 초기화
for i in range(len(layers) - 1):
self.layers.append({
'weights': np.random.randn(layers[i], layers[i + 1]),
'biases': np.zeros((1, layers[i + 1]))
})
# 손실 추적
self.train_loss = []
self.test_loss = []
def forward(self, X):
self.a = [X]
for layer in self.layers:
self.a.append(self.sigmoid(np.dot(self.a[-1], layer['weights']) + layer['biases']))
return self.a[-1]
def backward(self, X, y, learning_rate):
m = X.shape[0]
self.dz = [self.a[-1] - y]
for i in reversed(range(len(self.layers) - 1)):
self.dz.append(np.dot(self.dz[-1], self.layers[i + 1]['weights'].T) * self.sigmoid_derivative(self.a[i + 1]))
self.dz = self.dz[::-1]
for i in range(len(self.layers)):
self.layers[i]['weights'] -= learning_rate * np.dot(self.a[i].T, self.dz[i]) / m
self.layers[i]['biases'] -= learning_rate * np.sum(self.dz[i], axis=0, keepdims=True) / m
def sigmoid(self, x):
return 1 / (1 + np.exp(-x))
def sigmoid_derivative(self, x):
return x * (1 - x)
이 섹션에서는 신경망의 작동 방식에 중요한 조정을 가했으며, 임의의 층 수를 유연하게 지원하는 모델을 목표로했습니다. 변경된 사항은 다음과 같습니다:
먼저, 이전에 각 층의 노드 수를 정의했던 self.input, self.hidden, self.output 변수를 삭제했습니다. 이제 목표는 임의의 층 수를 관리할 수 있는 다목적 모델입니다. 예를 들어, 이전에 숫자 데이터셋에 사용했던 모델인 64개의 입력 노드, 64개의 은닉 노드 및 10개의 출력 노드를 사용하는 경우, 다음과 같이 설정할 수 있습니다:
nn = NeuralNetwork((layers = [64, 64, 10]));
이제 코드가 각 레이어를 세 번씩 순환하며 다른 목적으로 사용됨을 알 수 있습니다:
초기화 과정 중에는 모든 레이어의 가중치와 편향이 설정됩니다. 이 단계는 학습 프로세스를 위해 초기 매개변수로 네트워크를 준비하는 데 중요합니다.
순방향 패스 동안 활성화 self.a는 리스트에 수집됩니다. 입력 레이어의 활성화(본질적으로 입력 데이터 X)로 시작합니다. 각 레이어에 대해, np.dot(self.a[-1], layer['weights']) + layer['biases']를 사용하여 가중치 합과 편향을 계산하고 시그모이드 활성화 함수를 적용하여 결과를 self.a에 첨부합니다. 네트워크의 결과는 self.a의 마지막 요소로, 최종 출력을 나타냅니다.
역 전파 동안, 이 단계는 마지막 레이어의 활성화에 대한 손실의 도함수를 계산하고 출력 레이어의 오차 목록을 준비함으로써 시작합니다 (self.dz). 그런 다음 네트워크를 역방향으로 거슬러 올라가며 (reversed(range(len(self.layers) - 1))를 사용하여), 숨은 레이어에 대한 오차 항목을 계산합니다. 이 과정은 현재 오차 항목을 다음 레이어의 가중치와 점곱(역방향)하여 시그모이드 함수의 도함수로 비선형성을 처리하는 작업을 포함합니다.
class Trainer:
...
def train(self, X_train, y_train, X_test, y_test, epochs, learning_rate):
for _ in range(epochs):
self.model.forward(X_train)
self.model.backward(X_train, y_train, learning_rate)
train_loss = self.calculate_loss(y_train, self.model.a[-1])
self.train_loss.append(train_loss)
self.model.forward(X_test)
test_loss = self.calculate_loss(y_test, self.model.a[-1])
self.test_loss.append(test_loss)
마지막으로, NeuralNetwork 클래스의 변화에 따라 Trainer 클래스를 업데이트했습니다. 주요한 수정 사항은 특히 train 메서드에 있으며, 네트워크의 출력이 이제 self.model.a[-1]에서 가져온다는 점 때문에 훈련 및 테스트 손실을 다시 계산하는 방식입니다.
이러한 수정 사항은 우리의 신경망을 다양한 아키텍처에 적응할 수 있도록 할뿐만 아니라 데이터와 그래디언트의 흐름을 이해하는 중요성을 강조합니다. 구조를 간소화함으로써, 각종 작업에서 네트워크의 성능을 실험하고 최적화할 수 있는 능력을 향상시킵니다.
3: 향상된 학습을 위한 최적화 기법
신경망을 최적화하는 것은 그들이 배우는 능력을 향상시키고 효율적인 학습을 보장하며 최상의 버전으로 이끄는 데 중요합니다. 저희 모델이 얼마나 잘 수행되는지에 상당한 영향을 미치는 몇 가지 중요한 최적화 기술에 대해 알아보겠습니다.
3.1: 학습률
학습률은 손실 경사에 기반하여 네트워크의 가중치를 조정하는 제어 장치입니다. 이는 모델이 학습하는 속도를 결정하며 최적화 중에 취하는 단계가 얼마나 큰지 작은지를 결정합니다. 학습률을 적절하게 설정하면 모델이 빠르게 낮은 오차의 해결책을 찾을 수 있습니다. 그러나 올바르게 설정하지 않으면 모델이 수렴하는 데 시간이 오래 걸리거나 아예 좋은 해결책을 찾지 못할 수 있습니다.
너무 높은 학습률을 설정하면 모델이 최적해를 뛰어넘을 수 있어 불안정한 행동을 일으킬 수 있습니다. 이는 정확도나 손실이 훈련 중에 급격하게 변하는 것으로 나타날 수 있어요.
학습률이 너무 낮으면 훈련 과정이 지나치게 느리게 진행될 수 있어요. 이 경우, 훈련 손실이 시간이 지남에 따라 거의 변하지 않는 것을 볼 수 있어요.
관건은 훈련 및 검증 손실을 추적하면서 학습률이 어떻게 작동하는지에 대한 단서를 얻는 것이에요. 훈련 중에 일정 간격으로 이러한 손실을 기록하고 나중에 이를 플로팅하여 손실 landscape가 얼마나 매끄럽거나 불안정한지 보다 명확히 파악할 수 있어요. 우리의 코드에서는 이러한 메트릭을 추적하기 위해 Python의 logging 라이브러리를 사용하고 있어요. 이렇게 생겼답니다:
import logging
# Logger 설정
logging.basicConfig(level=logging.INFO)
logger = logging.getLogger(__name__)
class Trainer:
...
def train(self, X_train, y_train, X_val, y_val, epochs, learning_rate):
for epoch in range(epochs):
...
# 50 에폭마다 손실 및 검증 손실을 로그로 남깁니다
if epoch % 50 == 0:
logger.info(f'에폭 {epoch}: 손실 = {train_loss}, 검증 손실 = {val_loss}')
시작할 때, 우리는 훈련 업데이트를 캡처하고 표시하기 위해 로거를 설정했습니다. 이 설정을 통해 우리는 훈련 및 검증 손실을 매 50번째 에포크마다 기록하여 모델의 진행 상황에 대한 안정적인 피드백을 받을 수 있습니다. 이 피드백을 통해 손실이 잘 감소하고 있는지, 아니면 너무 불규칙하게 변동하는지 파악할 수 있어서 학습률을 조정해야 할 필요가 있을지도 모릅니다.
위의 코드는 훈련 및 검증 손실을 그래프로 플로팅하여 훈련 중에 손실이 어떻게 변화하는지 더 잘 이해할 수 있도록 해줍니다. 많은 반복에서 약간의 잡음이 예상되므로 부드러운(스무딩) 효과를 추가했습니다. 잡음을 부드럽게 처리하여 그래프를 더 잘 분석할 수 있도록 도와줄 것입니다.
이러한 방식을 따르면 훈련을 시작하면 로그가 나타나면서 우리의 진행 상황을 한 눈에 볼 수 있고 조정할 수 있는 정보를 제공하여 우리가 방향을 수정하는 데 도움이 될 것입니다.
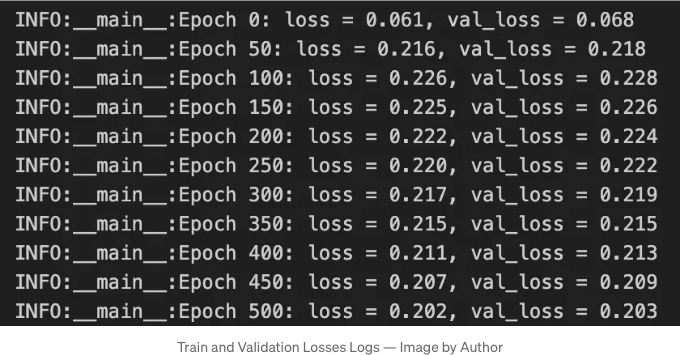
그런 다음, 훈련이 끝난 후 손실을 그래프로 그려볼 수 있습니다:
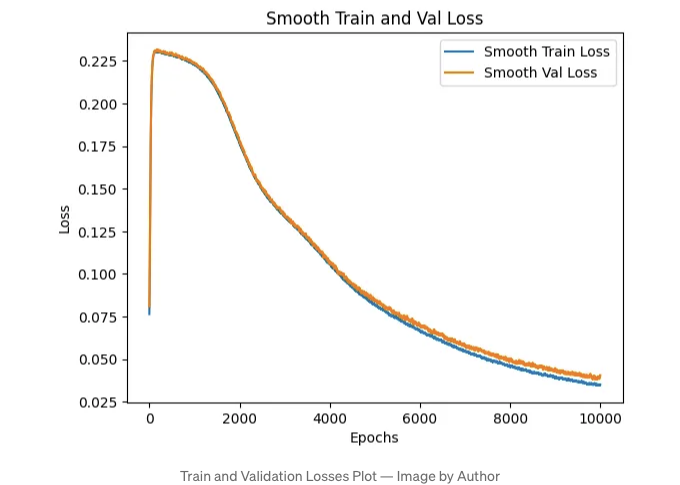
훈련 및 검증 손실이 꾸준히 감소하는 것을 보는 것은 좋은 신호입니다. 이는 에포크 수를 늘리고 학습률 스텝 크기를 증가시킨다면 잘 작동할 수 있다는 신호일 수 있습니다. 그러나 반대로 손실이 감소한 후 급상승하는 것을 관찰하면, 학습률 스텝 크기를 줄이는 것이 명백한 신호입니다. 그렇지만 재미있는 점이 있습니다: 에포크 0부터 50까지 우리의 손실이 어떤 이상한 일이 일어나고 있습니다. 우리는 그 부분을 확인하기 위해 다시 살펴보겠습니다.
그 달콤한 학습률의 최적값을 찾기 위해서는 학습률 앤달링 또는 적응형 학습률 기법과 같은 방법이 정말 유용할 수 있어요. 이러한 방법들은 학습률을 실시간으로 세밀하게 조정하여 훈련 중에 최적의 속도를 유지하도록 도와줘요.
3.2: 조기 중단 기법
조기 중단은 마치 안전망 같아요 — 유효성 검사 세트에서 모델의 성능을 보고, 더 이상 성능이 개선되지 않을 때 훈련을 중지하는 것이에요. 이는 과적합에 대한 안전 장치이며, 우리 모델이 이전에 본 적 없는 데이터에서도 잘 작동하도록 보장해줘요.
여기에 이를 실행하는 방법이 있어요:
- 검증 세트: 교육 데이터의 일부를 분리하여 검증 세트로 사용합니다. 이것은 중요합니다. 왜냐하면 이렇게 하면 멈춤 결정이 신선한 보이지 않는 데이터에 기반하기 때문입니다.
- 모니터링: 각 학습 에포크 후 모델이 검증 세트에서 어떻게 수행되는지 주시하세요. 성능이 향상되고 있나요, 아니면 정체되었나요?
- 멈춤 기준: 멈출 시점을 결정하세요. 일반적으로 "연속적으로 50번의 에포크 동안 검증 손실이 향상되지 않음"이 있습니다.
이를 위한 코드를 살펴보죠:
class Trainer:
def train(self, X_train, y_train, X_val, y_val, epochs, learning_rate,
early_stopping=True, patience=10):
best_loss = np.inf
epochs_no_improve = 0
for epoch in range(epochs):
...
# 조기 중단
if early_stopping:
if val_loss < best_loss:
best_loss = val_loss
best_weights = [layer['weights'] for layer in self.model.layers]
epochs_no_improve = 0
else:
epochs_no_improve += 1
if epochs_no_improve == patience:
print('조기 중단!')
# 최적의 가중치로 복원
for i, layer in enumerate(self.model.layers):
layer['weights'] = best_weights[i]
break
train 메서드에서 두 가지 새로운 옵션을 소개했습니다:
- early_stopping: 이는 조기 중단을 켜거나 끄는 여부를 결정하는 이진 플래그입니다.
- patience: 이는 훈련을 중단하기 전에 유효성 검사 손실이 향상되지 않은 라운드 수를 설정합니다.
우리는 가장 낮은 유효성 검사 손실을 현재까지 본 최저치로 설정하기 위해 best_loss를 무한대로 설정합니다. 한편, epochs_no_improve는 얼마 동안 유효성 검사 손실이 개선되지 않은 에포크 수를 기록합니다.
모델을 훈련하기 위해 각 에포크를 순회하는 동안에는 실제 훈련 단계(순방향 전파 및 역전파)가 여기에 자세히 나와 있지는 않지만 프로세스의 중요한 부분입니다.
매 에포크가 끝날 때마다 현재 에포크의 유효성 검사 손실(val_loss)이 best_loss보다 낮아졌다면, 이는 우리가 진전을 이루고 있다는 뜻입니다. 우리는 best_loss를 이 새로운 최솟값으로 업데이트하고, 또한 현재 모델 가중치를 best_weights로 저장합니다. 이렇게 하면 모델이 최상의 성능을 발휘한 시점의 스냅샷을 항상 가지게 됩니다. 그리고 우리는 방금 개선을 보았기 때문에 epochs_no_improve 카운트를 다시 0으로 재설정합니다.
만약 val_loss에 감소가 없다면, epochs_no_improve를 하나씩 증가시켜서 다른 epoch가 향상되지 않은 것으로 표시합니다.
만약 우리가 설정한 인내심 한계치에 epochs_no_improve 카운트가 달성하면, 모델이 더 나아질 가능성이 낮다는 신호로 조기 종료를 시작합니다. 메시지와 함께 알림을 표시하고, 모델의 가중치를 최적의 가중치인 best_weights로 되돌립니다. 그런 다음 학습 루프를 종료합니다.
이 접근 방식은 학습을 중단하는 균형있는 방법을 제공합니다. 모델에 학습의 공정한 기회를 제공하여 너무 일찍 중단하지 않으면서, 너무 늦지도 않아 시간을 낭비하거나 과적합의 위험을 가져올 수 있습니다.
3.3: 초기화 방법
신경망을 설정할 때, 가중치를 어떻게 시작하느냐에 따라 네트워크가 얼마나 잘, 그리고 얼마나 빨리 학습하는지가 달라질 수 있어요. 가중치를 초기화하는 몇 가지 다른 방법 – 랜덤, 영, Glorot(Xavier), 그리고 He 초기화 – 에 대해 알아봐요.
랜덤 초기화 랜덤 방식을 선택하면 주로 균일하거나 정규 분포에서 숫자를 추출하여 초기 가중치를 설정하는 것을 의미해요. 이러한 무작위성은 모든 뉴런이 동일한 위치에서 시작하지 않도록하여 네트워크가 학습함에 따라 서로 다른 것을 배울 수 있도록 도와줘요. 핵심은 적절한 분산을 선택하는 것인데, 너무 많으면 기울기가 폭발할 위험이 있고, 너무 적으면 사라질 수도 있어요.
weights = np.random.randn(layers[i], layers[i + 1]);
이 코드 라인은 표준 정규 분포에서 가중치를 추출하여 각 뉴런이 학습의 길로 나아갈 수 있도록 준비를 합니다.
장점: 뉴런이 서로 모방하는 것을 방지하는 간단한 방법입니다.
단점: 분산을 잘못 설정하면 학습 과정이 불안정해질 수 있습니다.
제로 초기화 모든 가중치를 0으로 설정하는 방법은 매우 간단합니다. 그러나 이 방법에는 주요 단점이 있습니다: 이로 인해 층의 모든 뉴런이 사실상 동일해집니다. 이러한 동일성으로 인해 네트워크의 학습이 저해될 수 있으며, 모든 층의 뉴런이 학습 중에 동일하게 업데이트될 수 있습니다.
weights = np.zeros((layers[i], layers[i + 1]));
마지막으로, 우리는 모두 0으로 채워진 가중치 행렬을 얻습니다. 깔끔하고 정돈되어 있지만, 네트워크를 통해 나아가는 모든 경로가 처음에는 동일한 가중치를 갖게 되어 학습 다양성을 위한 좋지 않은 결과를 초래할 수 있습니다.
장점: 구현이 매우 쉽습니다.
단점: 학습 과정을 제약시켜 네트워크의 성능이 보통 좋지 않게끔 만듭니다.
Glorot 초기화 시그모이드 활성화 함수를 사용하는 네트워크를 위해 설계된 Glorot 초기화는 네트워크 내 입력 단위와 출력 단위의 수에 기반하여 가중치를 설정합니다. 이 초기화는 활성화와 역전파된 그래디언트의 분산을 유지하고 vanishing 또는 exploding 그래디언트 문제를 방지하기 위해 레이어를 통해 전달됩니다.
글로럿 초기화에서의 가중치는 균일 분포나 정규 분포로 생성할 수 있습니다. 균일 분포를 사용하는 경우, 가중치는 [-a, a] 범위로 초기화됩니다. 여기서 a 값은:
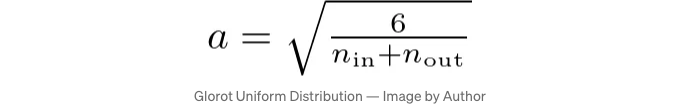
def glorot_uniform(self, fan_in, fan_out):
limit = np.sqrt(6 / (fan_in + fan_out))
return np.random.uniform(-limit, limit, (fan_in, fan_out))
weights = glorot_uniform(layers[i - 1], layers[i])
이 공식은 가중치가 균등하게 분포되고, 가져올 수 있으며, 좋은 기울기 흐름을 유지할 수 있도록 보장합니다.
정상 분포에 대한 정보입니다:
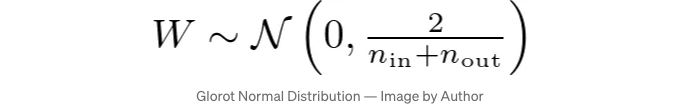
def glorot_normal(self, fan_in, fan_out):
stddev = np.sqrt(2. / (fan_in + fan_out))
return np.random.normal(0., stddev, size=(fan_in, fan_out))
weights = self.glorot_normal(layers[i - 1], layers[i])
이 조정은 시그모이드 활성화 함수를 사용하는 네트워크에서 적절하게 가중치를 유지합니다.
장점: 합리적인 범위 내 그라디언트 변화를 유지하여 심층 신경망의 안정성을 향상시킵니다.
단점: ReLU(또는 변형) 활성화를 사용하는 레이어에는 신호 전파 특성이 다르기 때문에 최적이 아닐 수 있습니다.
He 초기화 He 초기화는 ReLU 활성화 함수를 사용하는 레이어에 적합하게 설계되었으며, ReLU의 비선형 특성을 고려하여 가중치의 분산을 조정합니다. 이 전략은 특히 ReLU가 일반적으로 사용되는 깊은 신경망에서 그라디언트 흐름을 유지하는 데 도움이 됩니다.
Glorot 초기화와 마찬가지로, 가중치는 균등 분포 또는 정규 분포에서 선택할 수 있습니다.
균일 분포를 위해 가중치는 [-a, a] 범위를 사용하여 초기화됩니다. 여기서 a는 다음과 같이 계산됩니다:
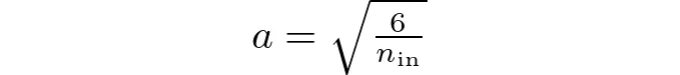
따라서 가중치 W는 균일 분포에서 추출됩니다:
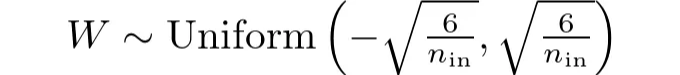
def he_uniform(self, fan_in, fan_out):
limit = np.sqrt(2 / fan_in)
return np.random.uniform(-limit, limit, (fan_in, fan_out))
weights = self.he_uniform(layers[i - 1], layers[i])
일반 분포를 사용할 때, 가중치는 다음과 같은 수식에 따라 초기화됩니다:
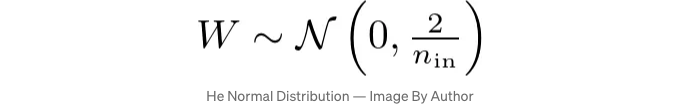
여기서 W는 가중치를, N은 정규 분포를, 0은 분포의 평균을, 그리고 2/n은 분산을 나타냅니다. n-in은 레이어로 들어오는 입력 단위의 수를 나타냅니다.
def he_normal(self, fan_in, fan_out):
stddev = np.sqrt(2. / fan_in)
return np.random.normal(0., stddev, size=(fan_in, fan_out))
weights = self.he_normal(layers[i - 1], layers[i])
양쪽 경우 모두 초기화 전략은 ReLU 활성화 함수의 특성을 반영하려고 합니다. 이 함수는 양수 입력에 대해 비활성화된 뉴런을 가지기 때문에 초기 가중치의 분산 조정은 깊은 네트워크에서 발생할 수 있는 그래디언트의 소실 또는 폭발을 방지하고 더 안정적이고 효율적인 훈련 과정을 촉진합니다.
장점: ReLU 활성화 함수를 사용하는 네트워크에서 그래디언트 크기를 유지하여 깊은 학습 모델을 용이하게 학습시킵니다.
단점: 특히 ReLU에 최적화되어 있어 다른 활성화 함수만큼 효과적이지 않을 수 있습니다.
이제 초기화를 소개한 후 NeuralNetwork 클래스가 어떻게 보이는지 살펴보겠습니다:
클래스 NeuralNetwork:
def __init__(self,
layers,
init_method='glorot_uniform', # 'zeros', 'random', 'glorot_uniform', 'glorot_normal', 'he_uniform', 'he_normal'
loss_func='mse',
):
...
self.init_method = init_method
# 레이어 초기화
for i in range(len(layers) - 1):
if self.init_method == 'zeros':
weights = np.zeros((layers[i], layers[i + 1]))
elif self.init_method == 'random':
weights = np.random.randn(layers[i], layers[i + 1])
elif self.init_method == 'glorot_uniform':
weights = self.glorot_uniform(layers[i], layers[i + 1])
elif self.init_method == 'glorot_normal':
weights = self.glorot_normal(layers[i], layers[i + 1])
elif self.init_method == 'he_uniform':
weights = self.he_uniform(layers[i], layers[i + 1])
elif self.init_method == 'he_normal':
weights = self.he_normal(layers[i], layers[i + 1])
else:
raise ValueError(f'알 수없는 초기화 방법 {self.init_method}')
self.layers.append({
'weights': weights,
'biases': np.zeros((1, layers[i + 1]))
})
...
...
def glorot_uniform(self, fan_in, fan_out):
limit = np.sqrt(6 / (fan_in + fan_out))
return np.random.uniform(-limit, limit, (fan_in, fan_out))
def he_uniform(self, fan_in, fan_out):
limit = np.sqrt(2 / fan_in)
return np.random.uniform(-limit, limit, (fan_in, fan_out))
def glorot_normal(self, fan_in, fan_out):
stddev = np.sqrt(2. / (fan_in + fan_out))
return np.random.normal(0., stddev, size=(fan_in, fan_out))
def he_normal(self, fan_in, fan_out):
stddev = np.sqrt(2. / fan_in)
return np.random.normal(0., stddev, size=(fan_in, fan_out))
...
적절한 가중치 초기화 전략을 선택하는 것은 효과적인 신경망 학습에 중요합니다. 무작위 및 영점 초기화는 기본적인 접근법을 제공하지만 항상 최적의 학습 동역학을 이끌어내지 않을 수 있습니다. 반면, Glorot/Xavier 및 He 초기화는 신경망 아키텍처 및 사용된 활성화 함수를 고려하여 딥 러닝 모델의 특정 요구 사항을 고려하는 더 소박한 솔루션을 제공합니다. 이러한 전략은 너무 빠른 학습과 너무 느린 학습 사이의 절충안을 균형있게 맞추어 더 신뢰할 수 있는 수렴 방향으로 학습 프로세스를 이끕니다.
3.4: 드롭아웃
Dropout은 신경망에서 오버피팅을 방지하기 위해 설계된 정규화 기술로, 훈련 단계에서 네트워크에서 임시로 그리고 무작위로 유닛(뉴런)과 해당 연결을 제거함으로써 사용합니다. 이 방법은 Srivastava 및 그 동료들이 2014 년 논문에서 고안한 간단하면서도 효과적인 방법으로 견고한 신경망을 훈련하는 데 사용됩니다.
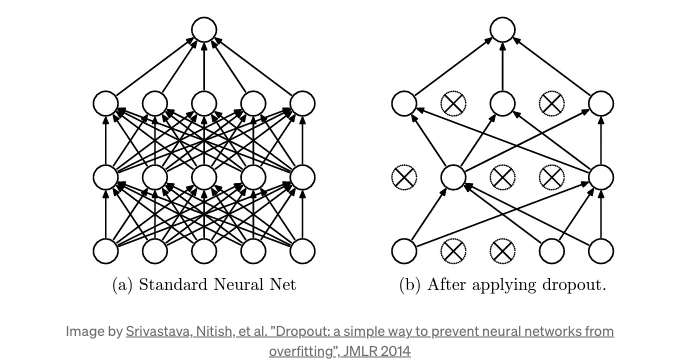
각 훈련 반복에서 각 뉴런(입력 단위 포함되지만 보통 출력 단위는 제외)은 일시적으로 "드랍아웃"될 확률 p를 가집니다. 이는 해당 뉴런이 이 전방 및 역방향 패스 동안 완전히 무시된다는 것을 의미합니다. 이 확률 p은 "드랍아웃 비율"로 불리며 성능을 최적화하기 위해 조절할 수 있는 하이퍼파라미터입니다. 예를 들어, 0.5의 드랍아웃 비율은 각 뉴런이 각 훈련 패스에서 계산에서 제외될 확률이 50% 라는 것을 의미합니다.
이 과정의 효과는 네트워크가 개별 뉴런의 특정 가중치에 덜 민감해진다는 것입니다. 이것은 예측을 할 때 개별 뉴런의 출력에 의존할 수 없으므로 네트워크가 뉴런들 사이에 중요성을 분산시키도록 장려합니다. 이는 실제로 가중치를 공유하는 신경망의 의사앙상블을 훈련하며, 각 훈련 반복에서 네트워크의 다른 "드랍아웃된" 버전이 포함됩니다. 시험 시간에는 드랍아웃이 적용되지 않고, 대신 가중치는 일반적으로 드랍아웃 비율 p에 의해 조정되어 더 많은 유닛이 활성화되었다는 사실을 균형 있게 합니다.
올바른 드롭아웃 비율 선택하기 드롭아웃 비율은 각 신경망 구조와 데이터셋에 대해 조정이 필요한 하이퍼파라미터입니다. 일반적으로, 숨겨진 유닛에 대해 시작점으로 0.5의 비율이 사용되며, 이는 원래 드롭아웃 논문에서 제안되었습니다.
높은 드롭아웃 비율 (1에 가까운 값)은 학습 중에 더 많은 뉴런이 제거되는 것을 의미합니다. 이는 네트워크가 데이터를 충분히 학습하지 못할 수 있어서, 훈련 데이터의 복잡성을 모델링하는 데 어려움을 겪어 과소적합을 초래할 수 있습니다.
반대로, 낮은 드롭아웉 비율 (0에 가까운 값)은 더 적은 뉴런이 제거되어 드롭아웃의 정규화 효과가 줄어들 수 있으며, 이는 모델이 훈련 데이터에서 잘 수행되지만 보이지 않는 데이터에서 성능이 나빠질 수 있는 과적합을 초래할 수 있습니다.
코드 구현 우리 코드에서 어떻게 보이는지 살펴보겠습니다:
class NeuralNetwork:
def __init__(self,
layers,
init_method='glorot_uniform', # 'zeros', 'random', 'glorot_uniform', 'glorot_normal', 'he_uniform', 'he_normal'
loss_func='mse',
dropout_rate=0.5
):
...
self.dropout_rate = dropout_rate
...
...
def forward(self, X, is_training=True):
self.a = [X]
for i, layer in enumerate(self.layers):
z = np.dot(self.a[-1], layer['weights']) + layer['biases']
a = self.sigmoid(z)
if is_training and i < len(self.layers) - 1: # apply dropout to all layers except the output layer
dropout_mask = np.random.rand(*a.shape) > self.dropout_rate
a *= dropout_mask
self.a.append(a)
return self.a[-1]
...
저희 신경망 클래스는 새로운 초기화 매개변수와 드롭아웃 정규화를 포함한 새로운 순전파 메서드로 업그레이드되었습니다.
dropout_rate : 이것은 훈련 중에 신경세포들이 네트워크에서 일시적으로 제거될 가능성을 결정하는 설정입니다. 오버피팅을 피하는 데 도움이 됩니다. 0.5로 설정함으로써 어떤 신경세포가 한 번의 훈련 라운드에서 "제거"될 확률이 50%라고 말하고 있습니다. 이 무작위성은 네트워크가 어떤 단일 신경세포에 너무 의존하지 않도록 보장하여 더 견고한 학습 과정을 촉진합니다.
is_training 부울 플래그는 네트워크가 현재 훈련되고 있는지를 알려줍니다. 이것은 훈련 중에만 드롭아웃이 발생해야 하므로 새 데이터에 대한 네트워크 성능을 평가할 때는 드롭아웃이 일어나서는 안 된다는 점이 중요합니다.
네트워크를 통해 데이터(X로 표시)가 전달되면, 네트워크는 들어오는 데이터와 레이어의 편향을 가중합(z)으로 계산합니다. 그런 다음 이 합계를 시그모이드 활성화 함수를 통해 활성화(a)로 변환하여 다음 레이어로 전달할 신호를 얻습니다.
하지만 훈련 중에 다음 레이어로 진행하기 전에 드롭아웃을 적용할 수 있습니다:
- is_training이 true이고 출력 레이어를 다루고 있지 않다면, 각 뉴런에 대해 주사위를 굴려 떨어뜨릴지 여부를 확인합니다. 이를 위해 무작위 수가 드롭아웃 비율을 초과하는지 확인하여 드롭아웃 마스크(모양은 a와 같은 배열)를 생성합니다.
- 이 마스크를 사용하여 a의 일부 활성화를 0으로 만들어 네트워크에서 일시적으로 뉴런을 제거하는 것을 흉내냅니다.
드롭아웃을 적용한 후(해당하는 경우), 생성된 활성화를 self.a에 추가하여 모든 레이어를 통해 활성화를 추적하는 리스트를 유지합니다. 이렇게 하면 신호를 그냥 한 레이어에서 다음 레이어로 무작정 이동시키는 것이 아니라, 네트워크가 더 견고하게 학습하도록 장려하는 기술을 적용하여 특정 경로의 뉴런에 지나치게 의존하지 않도록 합니다.
3.5: 그레이디언트 클리핑
그레이디언트 클리핑은 깊은 신경망을 훈련할 때 중요한 기술로, 특히 폭주하는 그레이디언트 문제를 해결할 때 주로 사용됩니다. 폭주하는 그레이디언트는 신경망의 매개변수에 대한 손실 함수의 미분이나 그레이디언트가 층을 거치면서 지수적으로 증가하여 훈련 중에 가중치에 대해 매우 큰 업데이트를 유도할 때 발생합니다. 이는 학습 과정을 불안정하게 만들 수 있으며, 종종 가중치나 손실에서 NaN 값의 형태로 나타나 수치 오버플로우 때문에 발산하여 모델이 해결책으로 수렴하지 못하도록 방해할 수 있습니다.
그레이디언트 클리핑은 값에 의한 클리핑과 법에 의한 클리핑 두 가지 주요 방법으로 구현할 수 있으며, 각각 폭주하는 그레이디언트 문제를 완화하는 전략을 가지고 있습니다.
값에 의한 클리핑 이 방법은 미리 정의된 임계값을 설정하고, 각 그레이디언트 구성 요소를 해당 임계값을 초과하는 경우 지정된 범위 내로 직접 클리핑하는 접근 방식입니다. 예를 들어, 임계값이 1로 설정되면, 1보다 큰 모든 그레이디언트 구성 요소를 1로 설정하고, -1보다 작은 모든 구성 요소를 -1로 설정합니다. 이는 모든 그레이디언트가 [-1, 1] 범위 내에 유지되도록 보장하여 너무 커지는 그레이디언트를 효과적으로 방지합니다.
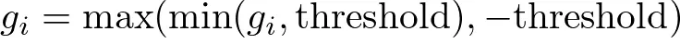
gi는 기울기 벡터의 각 구성 요소를 나타냅니다.
노름에 의한 클리핑 이 방법은 각 기울기 구성 요소를 개별적으로 클리핑하는 대신, 일정 임계값을 초과하는 경우 전체 기울기를 조절합니다. 이렇게 하면 기울기의 방향을 보존한 채 크기가 지정된 한도를 초과하지 않도록 할 수 있습니다. 이는 모든 매개변수를 통해 업데이트의 상대적 방향을 유지하는 데 특히 유용하며, 값에 의한 클리핑보다 학습 과정에 더 유익할 수 있습니다.
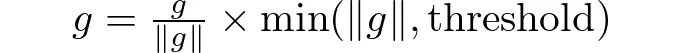
그래디언트 벡터를 나타내는 g이고 ∥g∥는 그 노름값입니다.
훈련에의 응용
class NeuralNetwork:
def __init__(self,
layers,
init_method='glorot_uniform', # 'zeros', 'random', 'glorot_uniform', 'glorot_normal', 'he_uniform', 'he_normal'
loss_func='mse',
dropout_rate=0.5,
clip_type='value',
grad_clip=5.0
):
...
self.clip_type = clip_type
self.grad_clip = grad_clip
...
...
def backward(self, X, y, learning_rate):
m = X.shape[0]
self.dz = [self.a[-1] - y]
self.gradient_norms = [] # 그래디언트 노름을 저장하는 리스트
for i in reversed(range(len(self.layers) - 1)):
self.dz.append(np.dot(self.dz[-1], self.layers[i + 1]['weights'].T) * self.sigmoid_derivative(self.a[i + 1]))
self.gradient_norms.append(np.linalg.norm(self.layers[i + 1]['weights'])) # 그래디언트 노름을 계산하고 저장
self.dz = self.dz[::-1]
self.gradient_norms = self.gradient_norms[::-1] # 리스트를 뒤집어서 레이어의 순서와 일치시킴
for i in range(len(self.layers)):
grads_w = np.dot(self.a[i].T, self.dz[i]) / m
grads_b = np.sum(self.dz[i], axis=0, keepdims=True) / m
# 그래디언트 클리핑
if self.clip_type == 'value':
grads_w = np.clip(grads_w, -self.grad_clip, self.grad_clip)
grads_b = np.clip(grads_b, -self.grad_clip, self.grad_clip)
elif self.clip_type == 'norm':
grads_w = self.clip_by_norm(grads_w, self.grad_clip)
grads_b = self.clip_by_norm(grads_b, self.grad_clip)
self.layers[i]['weights'] -= learning_rate * grads_w
self.layers[i]['biases'] -= learning_rate * grads_b
def clip_by_norm(self, grads, clip_norm):
l2_norm = np.linalg.norm(grads)
if l2_norm > clip_norm:
grads = grads / l2_norm * clip_norm
return grads
...
초기화 중에 이제 사용할 그래디언트 클리핑 유형(clip_type)과 그래디언트 클리핑 임계값(grad_clip)이 있습니다.
clip_type은 그레디언트를 값으로 자르는 경우에는 value, 또는 L2 노름에 의해 그레디언트를 자르는 경우에는 norm이 될 수 있습니다. grad_clip은 자르는 임계값이나 한계를 지정합니다.
그런 다음, 역전파 중에 함수는 네트워크의 각 레이어에 대한 그레디언트를 계산합니다. 가중치(grads_w)와 편향(grads_b)에 대한 손실의 미분 값을 각 레이어마다 계산합니다.
만약 clip_type이 value인 경우, np.clip을 사용하여 그레디언트를 [-grad_clip, grad_clip] 범위로 자릅니다. 이렇게 하면 그레디언트 성분이 이 한계를 초과하지 않도록 합니다.
만약 clip_type이 norm인 경우, 그레디언트의 노름이 grad_clip을 초과하는 경우 이 방향을 유지하면서 그에 대한 크기를 제한하기 위해 clip_by_norm 메서드가 호출됩니다.
클리핑 이후, 각 층의 가중치와 편향을 학습률에 의해 조정하는 데 그래디언트가 사용됩니다.
마지막으로, 그래디언트의 L2 노름이 지정된 clip_norm을 초과하는 경우 그래디언트를 스케일링하는 clip_by_norm 메서드를 만듭니다. 이 메서드는 그래디언트의 L2 노름을 계산하고, clip_norm보다 크면 그래디언트를 clip_norm까지 스케일 다운시키면서 방향을 유지합니다. 이는 그래디언트를 그들의 L2 노름으로 나누고 clip_norm을 곱해 달성됩니다.
그래디언트 클리핑의 장점 모델의 가중치에 대한 지나치게 큰 업데이트를 방지함으로써, 그래디언트 클리핑은 더 안정적이고 신뢰할 수 있는 훈련 과정에 기여합니다. 그래디언트의 계산이 큰 업데이트로 인해 불안정성을 초래할 수 있는 경우에도 손실 함수를 최소화하여 옵티마이저가 일관된 진전을 이룰 수 있도록 합니다. 이는 훈련하는 동안 그래디언트의 스케일이 큰 문제로 인해 불안정성 문제에 직면하는 순환 신경망(RNNs) 훈련과 같은 과제에서 특히 유용한 도구로 작용합니다.
그래디언트 클리핑은 신경망 훈련의 안정성과 성능을 향상시키는 간단하면서도 강력한 기술입니다. 그래디언트가 지나치게 커지지 않도록 보장함으로써, 훈련 불안정성(과적합, 과소적합, 수렴 속도 저하 등)의 문제를 피하고, 신경망이 효과적이고 효율적으로 학습하기 쉽도록 돕습니다.
4: 층의 최적 개수 결정하기
신경망을 설계하는 중요한 결정 중 하나는 올바른 층의 개수를 결정하는 것입니다. 이 측면은 네트워크의 데이터로부터 학습하고 새로운, 보지 못한 데이터를 일반화하는 능력에 상당한 영향을 미칩니다. 신경망의 깊이 - 얼마나 많은 층이 있는지 - 능력을 강화시키거나 과적합 또는 학습이 부족하다는 문제로 이어질 수 있습니다.
4.1: 층의 깊이와 모델 성능
신경망에 더 많은 층을 추가하면 학습 능력이 향상되어 데이터의 더 복잡한 패턴과 관계를 파악할 수 있습니다. 이는 추가적인 층이 입력 데이터의 보다 추상적인 표현을 만들 수 있기 때문에 단순한 기능에서 더 복잡한 조합으로 이동할 수 있습니다.
더 깊은 신경망은 복잡한 패턴을 모델링할 수 있지만, 추가적인 깊이가 오버피팅으로 이어지는 기묘한 지점이 있습니다. 오버피팅은 모델이 훈련 데이터를 너무 잘 학습하여 그 잡음까지 포함해 새로운 데이터에서 성능이 나빠지는 현상입니다.
궁극적인 목표는 훈련 데이터로부터 잘 학습하는 모델을 갖는 것뿐만 아니라 이 학습을 새로운 데이터에서도 정확하게 수행할 수 있는 범용성을 갖는 것입니다. 이를 위해서는 층의 깊이에 대한 적절한 균형을 찾는 것이 중요합니다. 너무 적은 층은 과소적합될 수 있고, 너무 많은 층은 오버피팅될 수 있습니다.
4.2: 적절한 깊이를 테스트하고 선택하는 전략
점진적인 접근 방식 간단한 모델부터 시작하여 점진적으로 층을 추가하고 검증 성능이 크게 향상될 때까지 관찰합니다. 이 접근 방식은 각 층이 전체 성능에 어떤 기여를 하는지 이해하는 데 도움이 됩니다.
모델의 성능을 판단하기 위한 기준으로 검증 세트(학습 중에 사용되지 않은 학습 데이터의 하위 집합)에서 모델이 일반화하는 능력을 향상시키는지 여부를 결정합니다.
정규화 기법 더 많은 레이어를 추가할 때 드롭아웃 또는 L2 정규화와 같은 정규화 방법을 사용하세요. 이러한 기법은 오버피팅의 위험을 줄일 수 있어 추가된 레이어가 모델의 학습 능력에 어떤 가치를 더하는지를 공정하게 평가할 수 있게 해줍니다.
학습 동태 관찰 더 많은 레이어를 추가할 때 학습과 검증 손실을 모니터링하세요. 이 두 지표 사이에 차이가 발생하는 경우 — 학습 손실이 감소하지만 검증 손실이 그렇지 않을 때 — 오버피팅을 나타낼 수 있으며, 현재 깊이가 지나칠 수 있다는 것을 시사할 수 있습니다.
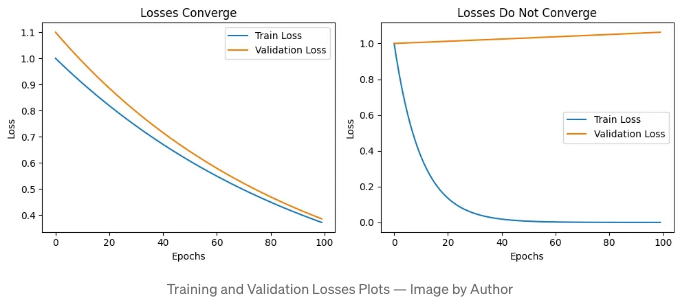
이 두 그래프는 기계 학습 모델을 훈련하는 과정에서 발생할 수 있는 두 가지 시나리오를 나타냅니다.
첫 번째 그래프에서는 훈련 손실과 검증 손실이 모두 감소하여 비슷한 값으로 수렴합니다. 이것은 이상적인 시나리오로, 모델이 잘 학습하고 적절하게 일반화되고 있음을 나타냅니다. 모델의 성능이 훈련 데이터와 보지 않은 검증 데이터 모두에서 향상되고 있는 것을 의미합니다. 이는 모델이 데이터를 과소적합하거나 과적합하지 않고 있다는 것을 시사합니다.
두 번째 그래프에서는 훈련 손실은 감소하지만 검증 손실이 증가합니다. 이는 과적합의 전형적인 징후입니다. 모델이 훈련 데이터를 너무 잘 학습하여 노이즈와 이상점을 포함하고 있으며 보지 않은 데이터에 대한 일반화를 실패합니다. 결과적으로, 검증 데이터에서의 성능이 시간이 지남에 따라 악화됩니다. 이는 모델의 복잡성을 줄이거나 정규화나 드롭아웃과 같은 과적합 방지 기술을 적용해야 할 수도 있다는 것을 나타냅니다.
자동화 아키텍처 탐색 신경망 아키텍처 탐색(NAS) 도구나 Optuna와 같은 하이퍼파라미터 최적화 프레임워크를 활용하여 서로 다른 아키텍처를 체계적으로 탐색하십시오. 이러한 도구는 다양한 구성을 평가하고 검증 지표에서 최상의 성능을 발휘하는 구성을 선택함으로써 최적의 레이어 수를 자동화할 수 있습니다.
신경망의 최적 레이어 수를 결정하는 것은 모델의 복잡성과 학습 및 일반화 능력을 균형있게 고려하는 세심한 프로세스입니다. 레이어 추가에 체계적인 방법론을 채택하고 교차 검증을 활용하며 정칙화 기법을 통합함으로써 특정 문제에 적합한 네트워크 깊이를 결정할 수 있습니다. 이를 통해 보이지 않는 데이터에 대한 모델 성능을 최적화할 수 있습니다.
5: Optuna을 활용한 자동 미세 튜닝
최적 성능을 달성하기 위해 신경망을 미세 조정하는 것은 다양한 하이퍼파라미터의 섬세한 균형을 찾는 과정으로, 종종 방대한 탐색 공간 속에서 바늘을 찾는 것처럼 느껴질 수 있습니다. 이때 Optuna와 같은 자동 하이퍼파라미터 최적화 도구가 필요합니다.
5.1: Optuna 소개
옵투나는 최적화 하이퍼파라미터 선택을 자동화하기 위해 설계된 오픈소스 최적화 프레임워크입니다. 이는 가장 효율적인 신경망 모델로 이어지는 매개변수 조합을 식별하는 복잡한 작업을 간단화합니다. 옵투나는 고급 알고리즘을 활용하여 최적화 하이퍼파라미터 공간을 보다 효과적으로 탐색하여, 필요한 계산 자원과 수렴 시간을 줄입니다.
5.2: 옵투나를 활용한 신경망 최적화 통합
옵투나는 베이지안 최적화, 트리 구조 파르젠 추정기, 진화 알고리즘 등 다양한 전략을 활용하여 하이퍼파라미터 공간을 지능적으로 탐색합니다. 이 접근 방식을 통해 옵투나는 가장 유망한 하이퍼파라미터를 빠르게 식별하여 최적화 과정을 크게 가속화할 수 있습니다.
옵투나를 신경망 훈련 워크플로우에 통합하는 것은 옵투나가 최소화 또는 최대화하려는 목적 함수를 정의하는 과정을 포함합니다. 이 함수에는 일반적으로 모델 훈련 및 검증 과정이 포함되며, 목표는 검증 손실을 최소화하거나 검증 정확도를 최대화하는 것입니다.
- 검색 공간 정의: 각 하이퍼파라미터 값 범위를 지정하여 Optuna가 탐색할 것입니다 (예: 레이어 수, 학습률, 드롭아웃 비율).
- 시험과 평가: Optuna는 모델을 훈련시키기 위해 매번 새로운 하이퍼파라미터 세트를 선택하는 시험을 진행합니다. 검증 세트에서 모델의 성능을 평가하고 이 정보를 사용하여 탐색을 안내합니다.
5.3: 실제 구현
import optuna
def objective(trial):
# 하이퍼파라미터 정의
n_layers = trial.suggest_int('n_layers', 1, 10)
hidden_sizes = [trial.suggest_int(f'hidden_size_{i}', 32, 128) for i in range(n_layers)]
dropout_rate = trial.suggest_uniform('dropout_rate', 0.0, 0.5) # 모든 레이어에 대한 단일 드롭아웃 비율
learning_rate = trial.suggest_loguniform('learning_rate', 1e-3, 1e-1)
init_method = trial.suggest_categorical('init_method', ['glorot_uniform', 'glorot_normal', 'he_uniform', 'he_normal', 'random'])
clip_type = trial.suggest_categorical('clip_type', ['value', 'norm'])
clip_value = trial.suggest_uniform('clip_value', 0.0, 1.0)
epochs = 10000
layers = [input_size] + hidden_sizes + [output_size]
# 신경망 생성 및 훈련
nn = NeuralNetwork(layers=layers, loss_func=loss_func, dropout_rate=dropout_rate, init_method=init_method, clip_type=clip_type, grad_clip=clip_value)
trainer = Trainer(nn, loss_func)
trainer.train(X_train, y_train, X_test, y_test, epochs, learning_rate, early_stopping=False)
# 신경망 성능 평가
predictions = np.argmax(nn.forward(X_test), axis=1)
accuracy = np.mean(predictions == y_test_labels)
return accuracy
# Study 객체 생성 및 목적 함수 최적화
study = optuna.create_study(study_name='nn_study', direction='maximize')
study.optimize(objective, n_trials=100)
# 최적 하이퍼파라미터 출력
print(f"Best trial: {study.best_trial.params}")
print(f"Best value: {study.best_trial.value:.3f}")
Optuna 최적화 프로세스의 핵심은 목적 함수입니다. 이 함수는 시험 목표를 정의하고 각 시험에 대해 Optuna에 의해 호출됩니다.
Heren_layers은 신경망의 은닉층의 수이며, 1에서 10 사이를 추천합니다. 층의 수를 변화시킴으로써 얕은 네트워크와 깊은 네트워크 아키텍처를 탐색할 수 있습니다.
hidden_sizes는 각 층의 크기(뉴런 수)를 저장하며, 32에서 128 사이의 숫자를 제안하여 모델이 다양한 용량을 탐색하게 합니다.
dropout_rate는 균일하게 0.0(드롭아웃 없음)에서 0.5 사이를 제안하여 시험을 통해 정규화 유연성을 가능케 합니다.
learning_rate는 로그 스케일로 1e-3에서 1e-1 사이를 제안하여, 학습률 최적화에 대한 공통적인 민감도로 인해 크기의 범위를 포괄하는 넓은 탐색 공간을 보장합니다.
신경망 가중치의 init_method은 일련의 일반적인 전략 중에서 선택됩니다. 이 선택은 훈련의 시작점과 수렴 동작을 영향을 줍니다.
clip_type과 clip_value는 그래디언트 클리핑 전략과 값으로, 값이나 노름을 기준으로 클리핑하여 폭발하는 그래디언트를 방지하는 데 도움이 됩니다.
그런 다음, 정의된 하이퍼파라미터를 사용하여 NeuralNetwork 인스턴스가 생성되고 훈련됩니다. 각 시행이 일정한 에포크 수동안 실행될 수 있도록 조기 중지가 비활성화되며, 일관된 비교를 보장합니다. 성능은 테스트 세트에서 모델의 예측 정확도를 기반으로 평가됩니다.
목적 함수와 NeuralNetwork 인스턴스가 정의된 후 Optuna 스터디로 이동할 수 있습니다. Optuna 스터디 객체는 목적 함수를 최대화(maximize)하는 데 사용되며, 이 문맥에서는 신경망의 정확도가 목적 함수입니다.
연구는 목적 함수를 여러 번 호출합니다(n_trials=100), 매번 옵튜나 내부 최적화 알고리즘에서 제안한 다른 하이퍼파라미터 세트로 호출합니다. 옵튜나는 시험 이력에 기반하여 지능적으로 제안을 조정하여 하이퍼파라미터 공간을 효율적으로 탐색합니다.
이 프로세스를 통해 모든 실험에서 찾은 가장 좋은 하이퍼파라미터 세트(study.best_trial.params)와 달성한 최고 정확도(study.best_trial.value)가 생성됩니다. 이 출력은 주어진 작업에 대한 신경망의 최적 구성에 대한 통찰을 제공합니다.
5.4: 혜택 및 결과
옵튜나를 통합함으로써, 개발자는 하이퍼파라미터 튜닝 프로세스를 자동화할뿐만 아니라 어떻게 다른 매개변수가 모델에 영향을 미치는지에 대한 깊은 통찰을 얻을 수 있습니다. 이를 통해 수동 실험을 통해 걸릴 시간의 일부로 최적화된, 더 견고하고 정확한 신경망이 생성됩니다.
옵투나의 체계적인 파라미터 조정 접근법은 신경망 개발에 새로운 수준의 정밀성과 효율성을 제공하여 개발자들이 더 높은 성능 표준을 달성하고 모델이 이룰 수 있는 한계를 뛰어넘을 수 있도록 돕습니다.
5.5: 한계
옵투나는 하이퍼파라미터 최적화에 강력하고 유연한 접근 방식을 제공하지만, 기계 학습 워크플로에 통합할 때 고려해야 할 몇 가지 한계점과 주의 사항이 있습니다.
계산 리소스 각 시도는 신경망을 처음부터 훈련해야 하므로, 특히 심층 신경망이나 대규모 데이터셋의 경우에는 계산 리소스가 많이 필요할 수 있습니다. 하이퍼파라미터 공간을 철저히 탐색하기 위해 수백 번이나 수천 번의 시도를 실행하는 것은 상당한 계산 리소스와 시간이 필요할 수 있습니다.
하이퍼파라미터 검색 공간 옵투나의 검색 효과는 검색 공간이 어떻게 정의되는지에 매우 의존합니다. 하이퍼파라미터 값의 범위가 너무 넓거나 문제와 제대로 일치하지 않으면 옵투나가 비최적 영역을 탐색하는 데 시간을 낭비할 수 있습니다. 반대로 검색 공간이 너무 좁으면 최적의 구성을 놓칠 수 있습니다.
하이퍼파라미터 수가 증가함에 따라 검색 공간이 기하급수적으로 증가하는데, 이를 "차원의 저주"라고 합니다. 이로 인해 옵투나가 공간을 효율적으로 탐색하고 합리적인 횟수의 시도 내에서 최적의 하이퍼파라미터를 찾는 것이 어렵다는 도전이 생길 수 있습니다.
평가 지표 목적 함수와 평가 지표의 선택은 최적화 결과에 상당한 영향을 미칠 수 있습니다. 모델의 성능이나 작업 목표를 적절히 포착하지 못하는 지표는 하이퍼파라미터 구성을 부적절하게 만들 수 있습니다.
모델의 성능 평가는 무작위 초기화, 데이터 섞기, 또는 데이터셋 내 잡음과 같은 요소로 인해 달라질 수 있습니다. 이러한 변동성은 최적화 과정에 잡음을 도입하여 결과의 신뢰성에 영향을 줄 수 있습니다.
알고리즘 제한사항 Optuna은 검색 공간을 탐색하기 위해 정교한 알고리즘을 사용하지만, 이러한 알고리즘의 효율성과 효과는 문제에 따라 다를 수 있습니다. 경우에 따라 특정 알고리즘이 지역 최적점으로 수렴하거나 하이퍼파라미터 공간의 특정 특성에 더 잘 맞도록 설정을 조정해야 할 수도 있습니다.
6: 결론
신경망의 세밀한 조정에 대해 심층적으로 살펴본 후에 우리가 걸어온 길을 돌아보는 좋은 시기입니다. 우리는 신경망이 어떻게 작동하는지에 대한 기본 사항부터 시작하여 그들의 성능과 효율성을 높이는 더 정교한 기술로 점진적으로 발전해왔습니다.
6.1: 다음 단계
우리는 신경망 최적화에 많은 영역을 다루었지만, 명백히 우리는 겨우 표면만 긁은 것 뿐입니다. 신경망 최적화의 영역은 방대하며 지속적으로 진화하고 있으며, 아직 탐험하지 않은 기술과 전략으로 넘쳐납니다. 다가오는 기사에서 더 심층적으로 파고들어 복잡한 신경망 구조와 더 높은 성능과 효율성을 끌어올릴 수 있는 고급 기술을 탐구할 예정입니다.
저희가 파헤치고자 하는 최적화 기술과 개념의 다양한 범위에는 다음과 같은 것들이 포함됩니다:
- 배치 정규화: 입력 레이어를 정규화해 활성화를 조정하고 스케일링하여 훈련 속도를 높이고 안정성을 향상시키는 방법입니다.
- 최적화 알고리즘: SGD 및 Adam을 포함한 최적화 알고리즘은 복잡한 손실 함수의 영역을 더 효과적으로 탐색할 수 있는 도구를 제공하여 더 효율적인 훈련 주기와 더 나은 모델 성능을 보장합니다.
- 전이 학습 및 파인 튜닝: 사전 훈련된 모델을 활용하여 새로운 작업에 적응시키면 훈련 시간을 크게 단축하고 데이터가 제한적인 작업에서 모델 정확도를 향상시킬 수 있습니다.
- 신경 아키텍처 탐색(NAS): 자동화를 사용하여 신경망을 위한 최상의 아키텍처를 발견함으로써 직관적이지 않은 효율적인 모델을 발견할 수 있습니다.
이러한 주제들은 단지 저희가 다루는 것 중 일부에 불과하며, 각각 고유한 이점과 도전을 제공합니다. 앞으로 나아가면서, 이러한 기술을 자세히 살펴보고, 언제 사용해야 하는지, 그들이 어떻게 작용하는지, 그리고 당신의 신경망 프로젝트에 미치는 영향에 대한 통찰력을 제공할 것을 목표로 합니다.
추가 자료
- “Deep Learning” - Ian Goodfellow, Yoshua Bengio, Aaron Courville 저: 깊은 학습 기술과 원리에 대한 깊이 있는 개요를 제공하는 이 근본적인 문헌은 고급 신경망 구조 및 최적화 방법을 다룹니다.
- “Neural Networks and Deep Learning: A Textbook” - Charu C. Aggarwal 저: 신경망에 대한 상세한 탐구를 제공하며, 깊은 학습과 그 응용에 중점을 둡니다. 신경망 디자인 및 최적화의 복잡한 개념을 이해하는 데 탁월한 자료입니다.
여기까지 왔습니다. 축하해요! 이 기사를 즐기셨다면 좋아요를 누르고 팔로우해주시면 감사하겠습니다. 저는 정기적으로 유사한 기사를 게시할 예정이니 많은 관심 부탁드립니다. 제 목표는 가장 인기 있는 알고리즘을 다시 처음부터 만들어 머신 러닝을 모든 사람이 접근 가능하도록 하는 것입니다.