TIL

빠른 푸리에 변환을 이용한 주식 시장 신호 분석 방법

빠른 푸리에 변환을 이용한 주식 시장 신호 분석 방법
TILPosted On Jul 9, 20247 min read

소개

금융 시장은 본질적으로 소음이 많고 예측할 수 없어서, 수익성 있는 기회를 식별하고 활용하려는 트레이더와 투자자에게 상당한 어려움을 줍니다.

이 복잡성을 해결하기 위해 현대 트레이더들은 수학적 및 통계적 기술을 활용하여 소음을 걸러내고 데이터의 기저 주기/트렌드를 더 명확히 이해하기 위한 다양한 기법을 사용합니다. FFT(Fast Fourier Transform) 알고리즘은 이러한 강력한 도구 중 하나로, 어떤 신호/파형을 주파수가 변하는 사인 성분들의 합으로 표현하는 데 사용되는 알고리즘입니다. 따라서 시간 영역에서 주파수 영역으로 신호를 변환합니다.

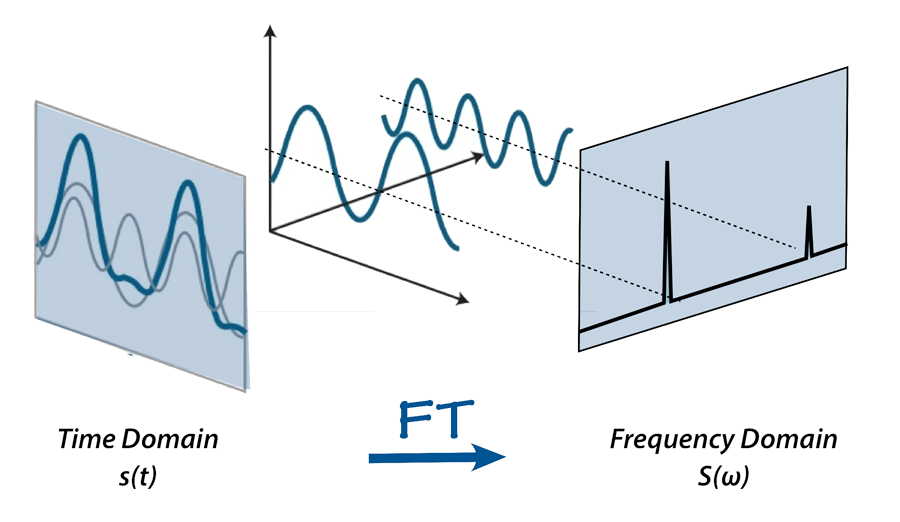
image

이 기사에서 논의하는 FFT 알고리즘은 신호 처리를 사용하여 가장 중요한 주파수를 감지하고 데이터에서 잡음을 제거합니다.

FFT를 사용하는 이유?

주기와 패턴 감지

주식 가격이나 거래량과 같은 금융 시계열은 다양한 경제 주기, 계절성 또는 투자자 행동으로 인해 주기적인 패턴을 나타내는 경우가 많습니다. 푸리에 변환은 이러한 주기와 해당 주파수를 식별하는 데 도움이 됩니다.

소음 필터링

금융 데이터는 종종 무작위 변동으로 인해 소음이 발생합니다. 데이터를 주파수 영역으로 변환하여 분석가들은 고주파 소음을 제거하여 중요한 저주파수 트렌드에 집중할 수 있습니다.

예측 모델링

주파수를 식별함으로써, 분석가들은 역사적인 패턴을 기반으로 미래 가격 변동이나 트렌드에 대한 예측을 할 수 있습니다.

기계 학습을 위한 기능 추출

Fourier 변환에서 얻은 주파수 구성 요소는 머신 러닝 모델에서 특징으로 사용되어 예측의 정확도를 향상시킬 수 있습니다.

코드 및 단계별 분석

노트북 설정 및 주식 데이터 수집

필요한 기본 주식 데이터 수집 및 데이터 프레임 조작을 위한 라이브러리 가져오기가 첫 번째 단계입니다.

또한, 분석 기간을 1년으로 설정하고 분석할 주식은 Tata Consultancy Services (TCS)입니다. 필요한 주식의 OLHCAV 데이터는 'df'라는 데이터 프레임에 저장되어 있습니다.

#라이브러리 가져오기
import pandas as pd
from pandas_datareader import data as pdr
import numpy as np
import math
import datetime
import scipy.stats as stats
import matplotlib.pyplot as plt
import yfinance as yfin
yfin.pdr_override()

# 분석 기간 설정
end_date = datetime.datetime.now()
start_date = end_date - datetime.timedelta(365)
ticker = 'TCS'

df = pdr.get_data_yahoo(ticker + '.NS', start = start_date, end = end_date)

FFT의 적용

np.fft.fft()을 사용하여 푸리에 변환을 수행할 것이며, np.fft.fftfreq()를 사용하여 주파수를 얻을 것입니다. 가장 중요한 주파수가 나타나는 때를 나타내기 위해 진폭 대 주기를 그래프로 그려볼 수 있습니다.

fft_result = np.fft.fft(df['Close'])
frequencies = np.fft.fftfreq(len(fft_result), d=1)  # assuming daily data, d=1
magnitude = np.abs(fft_result)
periods = 1 / frequencies

가격 및 주파수 영역 표현 시각화

아래의 주파수 플롯은 시계열 내에서 우세한 주파수를 강조합니다. 이러한 주파수는 역 FFT를 수행하거나 원래 시계열을 다시 만들거나 잡음을 줄인 버전을 생성하는 데 사용될 수 있습니다.

# 가격의 간단한 시각화
plt.figure(figsize=(10, 8))
plt.subplot(2, 1, 1)
plt.plot(df.index, df['Close'])
plt.title('TCS 시계열')
plt.xlabel('날짜')
plt.ylabel('가격')

# 주파수 도메인 표현
plt.subplot(2, 1, 2)
plt.plot(periods, magnitude)
plt.title('TCS의 FFT')
plt.xlabel('기간 (일)')
plt.ylabel('크기')
plt.xlim(0, max(periods[1:]))  # 중요한 주기를 보기 위한 x-축 제한 (큰 주기 무시)
plt.ylim(0, max(magnitude[1:]) * 1.1)  # 제로 주파수 구성요소 무시

plt.tight_layout()
plt.show()

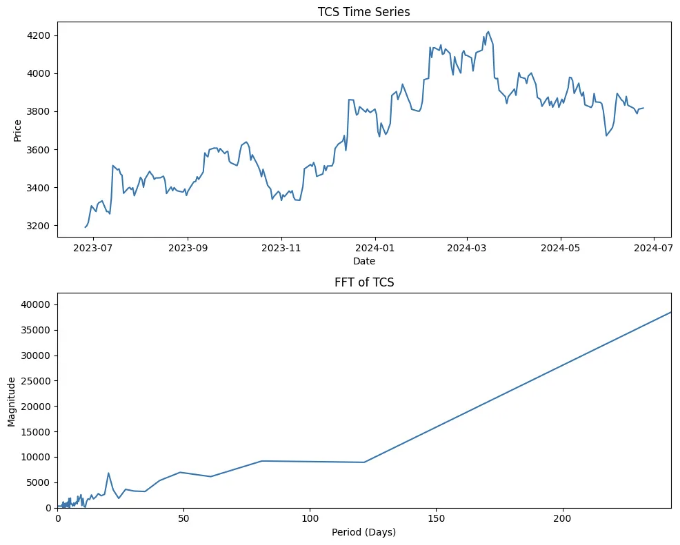
하지만, 이러한 우세 주파수의 중요성은 단순히 시계열을 재구성하는 데서 그치지 않습니다. 이들은 시계열 구조에 영향을 미치는 주요 경제 보고서나 거시경제 사건과 관련될 수 있습니다.

원래 주식 시장 데이터 복구하기

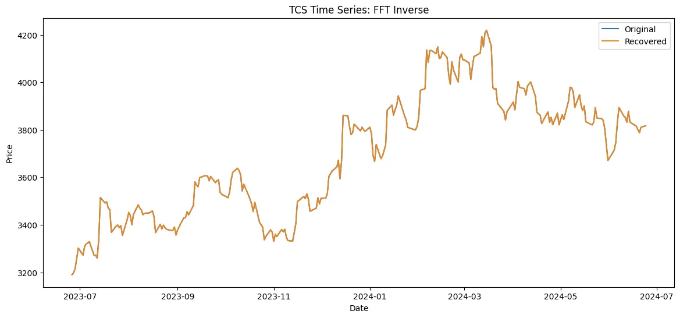
np.fft.ifft() 함수를 사용하여 원래의 시계열을 복원할 수 있습니다. 이 함수는 fft_results를 역변환합니다. 아래 그래프에서 볼 수 있듯이 완벽하게 재구성되었습니다.

recovered = np.fft.ifft(fft_result);
plt.figure((figsize = (14, 6)));
plt.plot(df.index, df["Close"], (label = "Original"));
plt.plot(df.index, recovered, (label = "Recovered"));
plt.title("TCS 시계열: FFT 역변환");
plt.xlabel("날짜");
plt.ylabel("가격");
plt.legend();
plt.show();

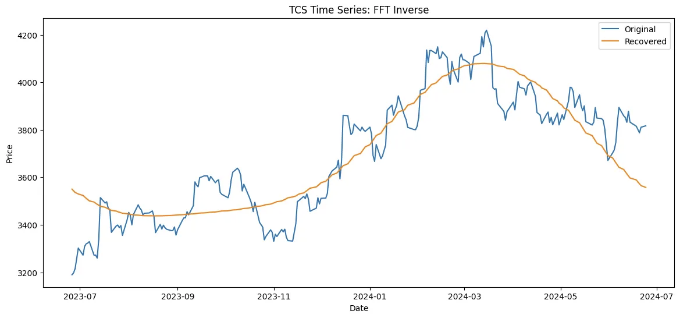
주요 주파수를 갖는 파형의 재구성

이것은 상위 25개 FFT 주파수만 사용하여 재구성된 신호를 생성합니다. 이것은 데이터의 노이즈 제거를 의미합니다.

dominant_periods = pd.Series(periods, (index = magnitude)).nlargest(25);
dominant_periods.to_frame("주기 (일)");
top_periods = dominant_periods.index;
top_fft_result = fft_result.copy();
top_fft_result[np.abs(frequencies) > 1 / top_periods.min()] = 0;
top_recovered = np.fft.ifft(top_fft_result);

plt.figure((figsize = (14, 6)));
plt.plot(df.index, df["Close"], (label = "원본"));
plt.plot(df.index, top_recovered, (label = "복원된"));
plt.title("TCS 시계열: FFT 역변환");
plt.xlabel("날짜");
plt.ylabel("가격");
plt.legend();
plt.show();

결론

이 문서에서 설명한 알고리즘은 산업 전문가들이 사용하는 분석을 지나치게 단순화한 것입니다. 성능을 개선하기 위해 일반적으로 매일 모델을 조정합니다.

도움이 되었기를 바라며, 여기에 GitHub 파일을 찾을 수 있습니다: https://github.com/karantha-kur/Signal-Analysis-Using-FFT/tree/main