통계학 시계열 분석 기본 개념 총정리

통계 및 수학

시각화 및 자세한 수학적 유도를 통한 시계열 분석 기초를 친절하게 소개합니다

요즘 시험을 위해 기본적인 통계적 시계열 분석에 대해 공부하고 있어요 [1]. 하지만 무서운 수학 공식들 때문에 머리에 남지 않는다구요. 그래서 자기상관, 자기상관성, 정상성 및 시계열 프로세스와 같은 기본적인 개념들을 시각화를 통해 정리하기로 했어요. 이 블로그에서는 시각화를 통해 이러한 개념을 가능한 한 자세히 설명하고 파이썬으로 구현해 볼 거에요.

목차

• 시계열이란 무엇인가? — 자기공분산, 자기상관 및 정상성

• 대표적인 시계열 과정

  • 2.1 백색 소음(white noise)
  • 2.2 자기회귀(AR) 과정

• 2.3 이동평균(MA) 프로세스

• 2.4 자기회귀 이동평균(ARMA) 및 ARIMA 프로세스

3. 시계열에 대한 통계 검정

• 3.1 증가된 디키-퓰러(ADF) 검정

-3.2 더빈-왓슨 검정

1. 시계열 데이터란? — 자기공분산, 자기상관 및 정상성

이름에서 알 수 있듯이 시계열은 시간과 관련이 있습니다. 시간이 흐름에 따라 관측된 데이터를 시계열 데이터라고합니다. 예를 들어, 심박수 모니터링, 일일 최고 기온 등이 있습니다. 이러한 예는 규칙적인 간격으로 관측되지만 시간이 불규칙한 간격으로 관측되는 시계열 데이터도 있습니다. 예를 들어, 일중 주식 거래, 임상 시험 등이 있습니다. 이 블로그는 규칙적인 간격으로 관측되는 단일 변수(일변량 시계열)의 시계열 데이터를 사용할 것입니다. 수학적으로 시계열은 다음과 같이 정의될 수 있습니다:

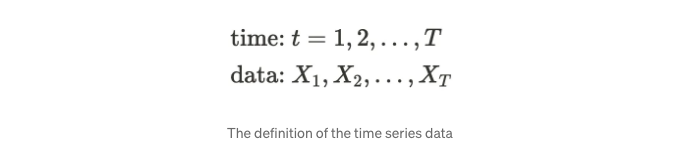
만약 Xₜ를 랜덤 변수로 간주한다면, 관측 시점 t에 따라 평균과 분산을 정의할 수 있습니다.

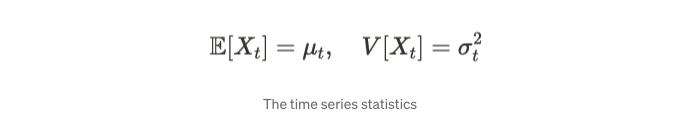
시계열 데이터의 경우, 과거와 현재 데이터를 비교해보고 싶을 수 있습니다. 이를 위해 자기공분산과 자기상관이라는 두 가지 필수 개념이 추가 논의를 위해 필요합니다. 그러니 이제 그것들을 자세히 살펴봅시다!

자기공분산

기술적으로 자기공분산은 공분산과 같습니다. 공분산은 다음과 같은 공식을 갖습니다:

이 경우, 공분산은 두 변수 X와 Y 간의 관계를 계산합니다. 표본 공분산을 계산할 때는 각 관측치와 평균의 차이를 n-1로 나누는 것에 유의하세요. 자기공분산의 경우 이전 관측치와 현재 관측치 간의 표본 공분산을 계산합니다. 공식은 아래와 같습니다:

헤이지는 래그로 불리며, 래그된 X는 h만큼 이동된 직전 X 값입니다. 공분산과 동일한 수식을 가지고 있는 것을 볼 수 있습니다.

자기상관

자기상관은 자기상관과 마찬가지로 상관 관계를 나타내며, 자기공분산과 같습니다. 상관 계수 공식은 다음과 같습니다.

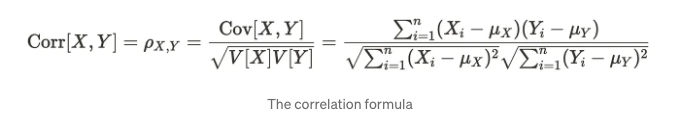
상관관계는 변수 X와 Y의 표준 편차로 공분산을 나누어 계산됩니다. 상관관계는 정규화된 공분산과 유사하게 생각할 수 있습니다. 자기 상관관계의 경우, 이전 및 현재 관측치 사이의 상관관계를 계산합니다. 여기서 h는 이 공식에서의 지연을 나타냅니다.

두 변수 X와 Y가 긍정적인 관계를 가질 때, 공분산 및 상관관계가 더 높은 양수 값을 가집니다. 자기공분산과 자기상관관계는 어떨까요? 시각화를 통해 확인해보겠습니다.

첫 번째 예제에서는 AR(1) 과정에서 데이터를 생성했습니다(나중에 자세히 살펴보겠습니다). 이는 잡음이 섞인 데이터처럼 보입니다.

아래 표는 Markdown 형식으로 변경되었습니다.

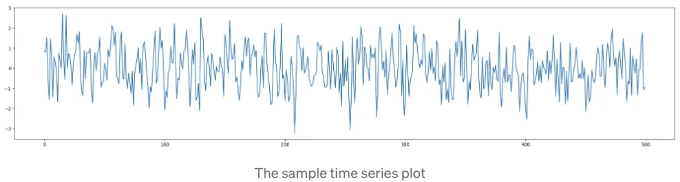
이 경우, 자기상관 및 자기상관도 그래프는 아래와 같습니다. x축은 래그(lag)를 나타냅니다.

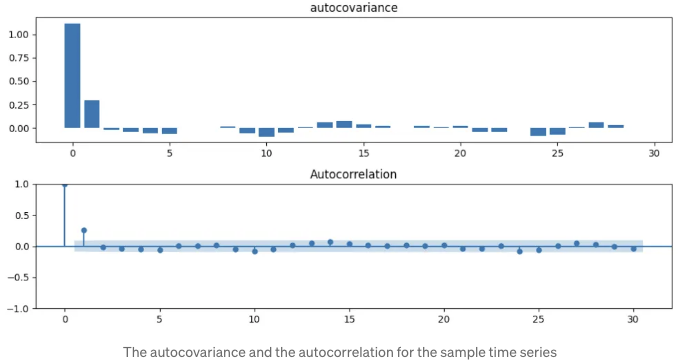
자기상관 및 자기상관도가 비슷한 경향을 보입니다. 따라서, 자기상관은 정규화된 자기상관으로 볼 수 있습니다.

다음 예제에서는 AirPassengers [4]와 같은 실제 데이터를 사용할 것입니다. AirPassengers 데이터는 명확한 상승 경향을 보입니다.

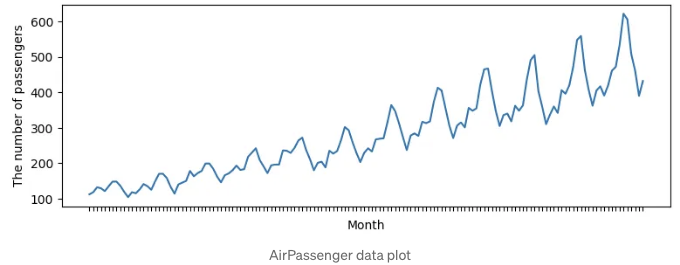
이 경우, 자기공분산 및 자기상관도 그래프는 아래와 같습니다. x 축은 지연을 나타냅니다.

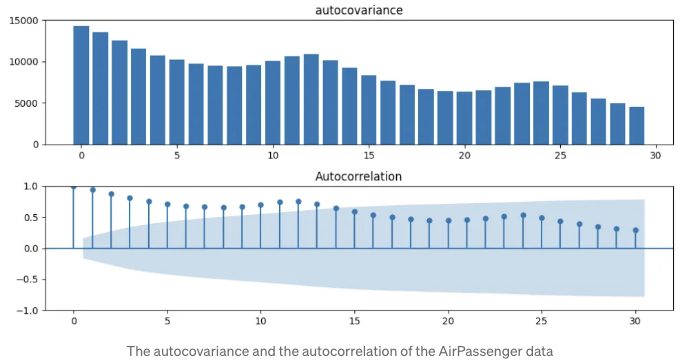
비슷하게, 자기 공분산과 자기 상관은 비슷한 경향을 가집니다. 이 데이터는 첫 번째 예제보다 더 많은 상관관계와 더 큰 지연을 가지고 있습니다.

이제 두 가지 주요 개념인 자기 공분산과 자기 상관에 대해 이해했습니다. 다음으로, '정상성(stationarity)'이라는 새로운 개념에 대해 이야기해보겠습니다. 정상성을 갖는 시계열은 평균, 분산 및 공분산과 같은 데이터 속성이 관측 시간에 의존하지 않음을 의미합니다. 정상성에는 다음 두 가지 유형이 있습니다:

• 약한 정상성(2차 정상성)
• 엄격한 정상성(강한 정상성)

정의를 확인해 봅시다.

1. 약한 정상성(2차 정상성)

위 과정은 약한 정상성, 2차 정상성 또는 공분산 정상성이라고 불리는 관계를 가지고 있습니다. (많은 방법으로 불릴 수 있습니다.)

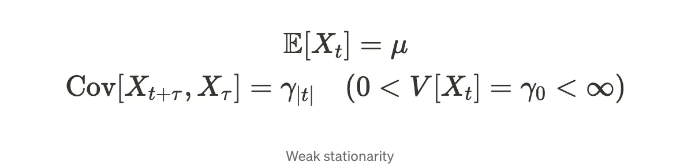
여기서 µ는 상수이고 𝛾ₜ는 𝛕에 의존하지 않습니다. 이러한 공식들은 평균과 분산이 시간에 따라 안정적이며, 공분산은 시간 지연에 의해 결정된다는 것을 보여줍니다. 예를 들어, 이전 단락의 첫 번째 예제는 약한 정상성을 갖습니다.

2. 엄격한 정상성(강한 정상성)

Fx(・)로 결합 밀도 함수를 나타낼 때, 엄격한 정상성은 다음과 같이 설명됩니다:

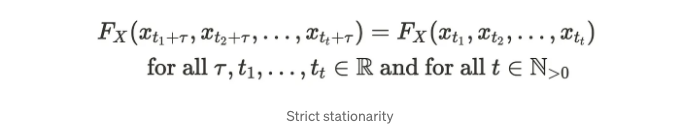
모든 시계열 데이터의 결합 분포가 시간 변화에 대해 불변일 때, 해당 시계열은 엄격한 정상성을 갖습니다. 엄격한 정상성은 약한 정상성을 함축합니다. 이 특성은 현실 세계에서 매우 제한적입니다. 따라서 많은 응용 프로그램은 약한 정상성에 의존합니다.

시계열 데이터가 정상인지 확인하는 몇 가지 통계적 검정 방법이 있습니다. 2장에서 대표적인 시계열 프로세스를 배우면 보다 이해하기 쉬울 것입니다. 그래서 이를 3장에서 소개하겠습니다.

2. 대표적인 시계열 프로세스

이제부터 흰 잡음(white noise), 자기회귀(AR), 이동평균(MA), ARMA, ARIMA와 같은 대표적인 시계열 프로세스를 살펴볼 것입니다.

2.1 흰 잡음

시계열 데이터가 다음 특성을 가질 때 해당 시계열 데이터는 화이트 노이즈를 가지고 있습니다.

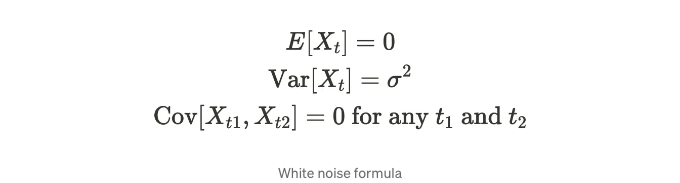
화이트 노이즈는 평균이 0이고, 분산이 시간 단계별로 동일합니다. 게다가 공분산이 0이며, 시계열과 그 시간 지연된 버전은 상관 관계가 없음을 의미합니다. 따라서 자기상관도는 0을 가집니다. 주로 시계열 회귀 분석에서 잔차 항이 만족해야 하는 가정으로 사용됩니다. 화이트 노이즈의 플롯은 아래와 같이 보입니다.

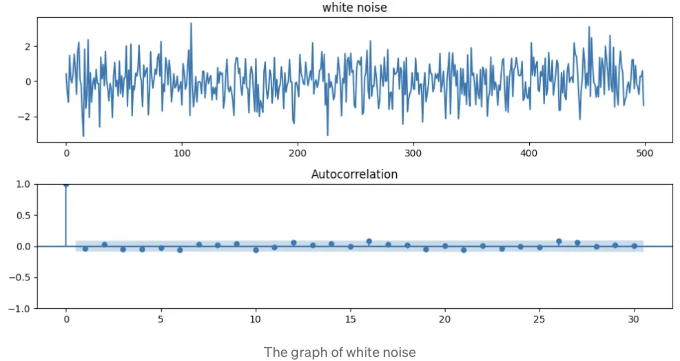
표 태그를 Markdown 형식으로 변환할 수 있습니다.

Uₜ이 백색 잡음이라고 가정하며, 𝜙은 한 단계 이전 값에 해당하는 알려지지 않은 매개변수입니다. Uₜ는 충격(shock)이라고도 불립니다. 과거 단계로 수식 (1)을 해결할 때 아래의 공식을 얻을 수 있습니다.

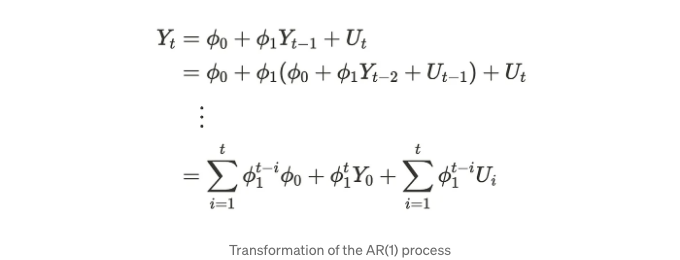
위 공식에서 𝜙ᵗ₁는 Y 시리즈에만 영향을 미칩니다. 따라서 아래의 사항을 깨달을 수 있습니다:

• 만약 |𝜙₁| ` 1이면, 단계가 지남에 따라 과거 값의 영향이 점점 작아집니다.
• 만약 |𝜙₁| = 1이면, 과거 값의 영향은 시차(Lags)에 관계없이 일정합니다.
• 만약 |𝜙₁| ` 1이면, 과거 값의 영향이 단계가 지남에 따라 현재 값에 영향을 줍니다.

각 케이스의 시각화를 확인해 봅시다.

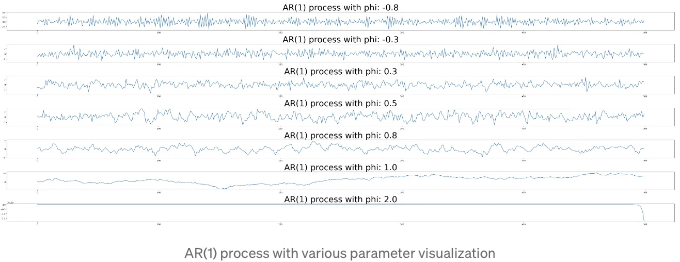
𝜙₁의 값이 커질수록 현재 스텝이 이전 스텝의 값에 따라 이루어집니다. 따라서 값이 증가함에 따라 부드러워 보이며, 𝜙₁ = 1이 될 때까지 값이 증가합니다. 𝜙₁가 1보다 큰 값일 때는 값이 무한대로 증가하므로 시리즈가 최종 그래프처럼 보입니다.

|𝜙₁| ` 1인 경우 약간의 정상 프로세스가 있습니다. AR(1) 프로세스가 약한 정상성을 만족할 때 평균과 공분산은 다음과 같습니다:

평균에 대해서는 시간에 따라 평균을 일정하게 사용합니다. 화이트 노이즈가 평균이 0이라는 사실을 이용하여 다음과 같은 공식을 유도할 수 있습니다.

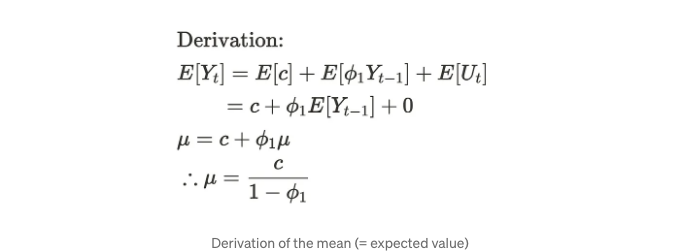
공분산에 대해서는 먼저 공식 (1)을 변경해야 합니다.

Then, we need to derive the variance and the covariance in this order. For the variance, we can derive it by taking a square of the above derived formula.

For the covariance, we can derive it by multiplying the subtraction of the previous step value and the mean.

AR(p) process를 비슷하게 고려할 수 있습니다.

보통, AR(p) 과정은 다음 조건(5)(6)을 만족할 때 약정상태(weak-stationary)가 될 수 있습니다.

공식 (5)와 (6)은 모든 공식 (5)의 루트가 단위 원 밖에 있어야 함을 의미합니다. p 번을 아무리 확장해도 결국 현실 세계에서의 여러 이전 단계들을 생각하는 것이 충분합니다.

2.3 이동 평균 (MA) 프로세스

이동 평균(MA) 프로세스는 현재와 이전 충격의 합으로 이루어져 있습니다. MA 프로세스에는 이전 잔차 또는 충격(Uₜ)의 수를 나타내는 순서(order)가 있습니다. 이를 MA(순서)로 표기합니다. 간단히, MA(1) 프로세스를 살펴봅시다. 다음 공식이 MA(1) 프로세스를 나타냅니다.

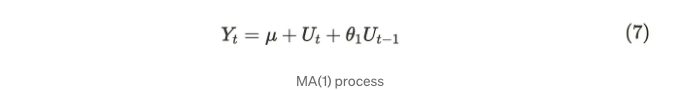
Uₜ가 백색 잡음이라고 가정하고, θ₁은 1단계 전 완강을 나타내는 알려지지 않은 파라미터입니다. MA(1) 과정은 백색 잡음으로 구성되어 있기 때문에 평균은 항상 µ입니다. 반면, 분산 및 공분산은 다음과 같이 유도될 수 있습니다:

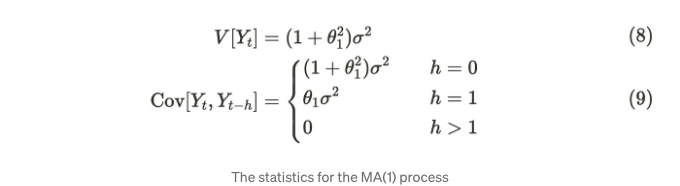
분산은 다음과 같이 유도할 수 있습니다:

마찬가지로, 공분산을 다음과 같이 유도할 수 있습니다:

화이트 노이즈는 각 변수가 다른 변수와 독립적이라고 가정하므로 이를 취소할 수 있습니다. 따라서 MA(1) 프로세스는 어떤 매개변수 θ₁에 대해서도 약한 정상 프로세스입니다. 이제 시각화를 통해 이를 확인해보겠습니다.

아래와 같이 보시다시피, 평균과 분산은 AR(1) 프로세스와 비교했을 때 동일해 보입니다. 파라미터 값이 증가할수록 시리즈가 상대적으로 부드러워집니다. MA(1) 프로세스와 백색 잡음의 분산이 다르다는 점을 참고해 주세요.

일반적으로 MA(q) 프로세스도 약정상태(weak-stationary)입니다.

평균과 공분산은 다음과 같이 정의할 수 있습니다.

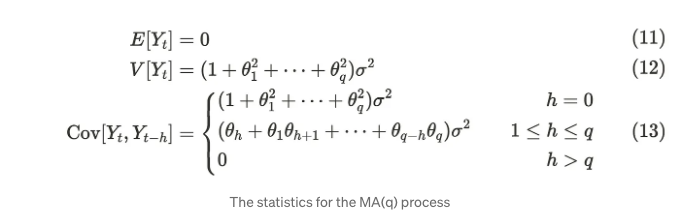
실제 세계에서는 AR 과정과 같은 몇 가지 이전 단계를 고려하는 것이 충분합니다.

2.4 자기회귀 이동평균(ARMA) 과정 및 ARIMA 과정

자신의 이름에서 알 수 있듯이 자기회귀 이동 평균(ARMA) 과정은 AR 및 MA 과정을 결합합니다. 직관적으로 ARMA 과정은 서로의 약점을 보완하고 데이터를 더 유연하게 나타낼 수 있습니다. 수학적 표현은 다음과 같습니다:

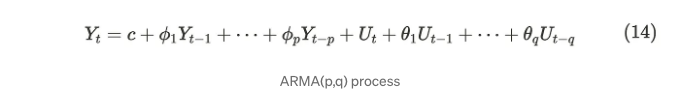
우리는 ARMA 과정을 ARMA(p, q)로 표시합니다. 매개변수 p와 q는 AR 및 MA 과정의 매개변수에 해당합니다. MA 과정은 항상 약한 정상성을 갖기 때문에 ARMA 과정의 약한 정상성은 AR 부분에 따라 달라집니다. 따라서, 식 (14)의 AR 부분이 식 (5)(6)을 만족하면 약한 정상성을 갖습니다.

시각화를 통해 ARMA 과정이 어떻게 보이는지 확인해보겠습니다. AR(p=1, q=1) 과정은 다음과 같이 보입니다:

AR(p=3, q=2) 프로세스는 아래 그래프와 같이 나타납니다.

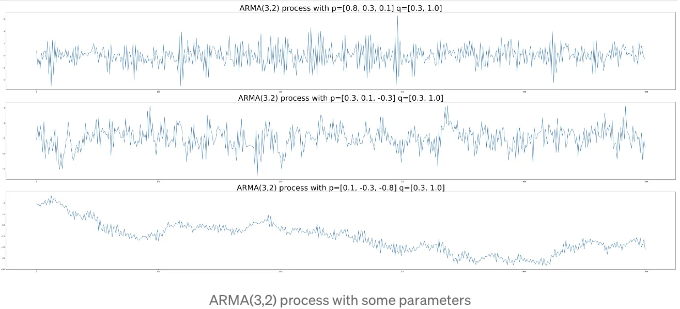
보시다시피, AR 및 MA 프로세스만 사용했을 때보다 더 복잡한 데이터 구조를 잘 파악할 수 있습니다. 매개변수 값이 증가할수록 그래프가 더 부드러워집니다.

마침내, Autoregressive-integrated-moving average(ARIMA) 프로세스는 ARMA 프로세스와 일부를 공유합니다. 차이점은 ARIMA에 통합된 부분 (I)이 있다는 것입니다. 통합된 부분이란 데이터를 평상태로 만들기 위해 차이를 몇 번 해야 하는지를 의미합니다. 이게 무슨 의미일까요? 먼저, 미분 연산자 ∇를 다음과 같이 정의합니다:

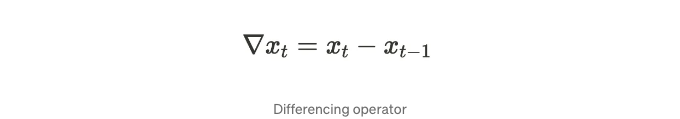
더 많이 차이를 원할 때, 우리는 반복하여 거듭제곱으로 확장할 수 있습니다:

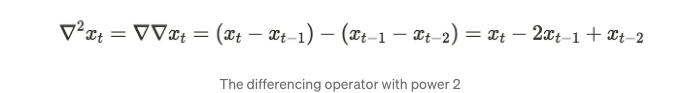
이제 차이 매개변수를 사용하여 ARIMA(p, d, q) 프로세스를 정의할 수 있습니다.

p는 AR 프로세스의 순서이고, d는 차별화를 할 횟수이며, q는 MA 프로세스의 순서입니다. 따라서 데이터를 차별화한 후 ARIMA 프로세스는 ARMA 프로세스가 됩니다. ARIMA 프로세스는 시계열에서 평균이 다른 경우 유용합니다. 즉, 시계열이 정상적이지 않을 때 사용됩니다. AirPassengers 데이터 세트를 기억해 주세요. 이 데이터 세트는 시리즈 전체에서 동일한 평균이 없습니다. 이 시리즈에 nabla를 적용하면 그래프가 다음과 같이 보입니다:

오른쪽 그래프의 평균은 왼쪽 그래프의 원본 데이터와 비교하여 시계열에서 안정적으로 보입니다. 이제 미분을 한 후 ARMA 프로세스를 적합시키고 싶습니다. 그러나 문제가 있습니다. 파라미터를 어떻게 정의해야 할까요? 다음과 같은 몇 가지 방법이 있습니다.

• MA 프로세스의 순서(q)를 결정하기 위해 자기상관 함수(ACF) 플롯을 사용하고 AR 프로세스의 순서(p)를 결정하기 위해 부분자기상관 함수(PACF) 플롯을 사용합니다.
• AIC 또는 BIC를 사용하여 최적의 적합 파라미터를 결정합니다.

첫 번째 방법에 따르면 ACF와 PACF 플롯을 사용하여 MA 및 AR 프로세스의 순서를 결정합니다. PACF도 자기상관이지만 Yₜ와 Yₜ+ₖ 사이의 간접적 상관을 0 n k 범위를 통해 제거합니다. 더 자세한 내용은 강의 pdf [5][6]를 참조하실 수 있습니다. 그러나 종종 플롯만으로는 파라미터를 결정할 수 없을 때가 있습니다. 그러므로 두 번째 방법을 사용하는 것을 권장합니다. AIC와 BIC는 다른 모델에 비해 모델 품질을 추정하는 데 사용되는 정보 기준입니다. 라이브러리 pmdarima [7] 덕분에 우리는 위의 정보 기준을 기반으로 최적의 파라미터를 쉽게 찾을 수 있습니다. 예를 들어, AirPassengers 데이터를 추정하기 위해 pmdarima를 사용할 때 결과는 다음과 같습니다.

# 스텝바이스 자동-ARIMA 적합
arima = pm.auto_arima(y_train, start_p=1, start_q=1,
                             max_p=3, max_q=3, # m=12,
                             seasonal=False,
                             d=d, trace=True,
                             error_action='ignore',  # 주문이 작동하지 않는 경우 알 필요 없음
                             suppress_warnings=True,  # 수렴 경고가 없으면 안됨
                             stepwise=True)  # 스텝바이스로 설정
arima.summary()

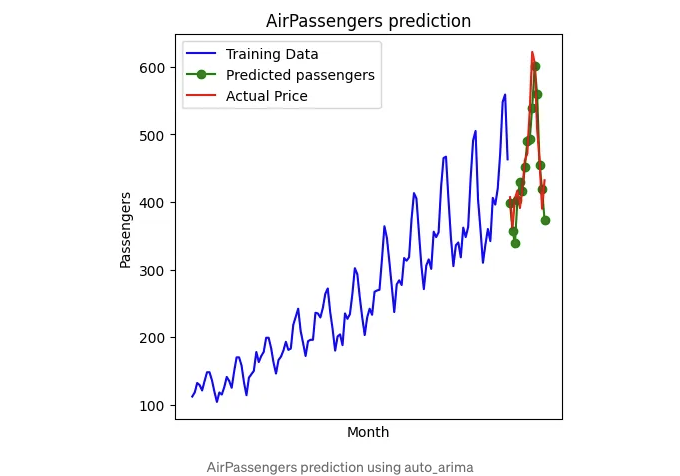
몇 줄만 써도 좋은 품질로 데이터를 맞출 수 있고 예측할 수 있습니다. 게다가, pmdarima는 SARIMA와 같은 고급 모델을 사용하여 시계열을 추정할 수 있습니다. 따라서 pmdarima는 실용적인 사용 사례에서 매우 유용합니다.

3. 시계열을 위한 통계 테스트

마지막 섹션에서는 시계열을 위해 사용되는 두 가지 유명한 통계 테스트를 소개하겠습니다. 이러한 테스트는 데이터가 정상 상태인지 또는 잔차 항이 자기상관성을 가지고 있는지 확인하기 위해 자주 사용됩니다. 각 테스트에 들어가기 전에, 단위근이라는 중요한 개념이 있습니다. 시계열에 단위근이 있는 경우 정상 상태가 아닙니다. 따라서 AR(p) 프로세스가 식(5)의 적어도 하나의 근이 1과 같다면, AR(p) 프로세스가 정상 상태가 아님을 의미하므로 AR(p) 프로세스에는 단위근이 있다고 할 수 있습니다. 이 개념을 사용하여 몇 가지 통계 테스트가 있습니다.

3.1 Augmented Dickey-Fuller(ADF) test

증강 딕키-풀러(ADF) 검정은 주어진 일변량 시계열에 단위근이 존재하는지를 평가합니다.

ADF 검정은 아래의 공식을 사용합니다. 이 공식은 공식(10)에서 유도되었습니다.

그럼, 다음은 귀무 가설과 대립 가설을 설정합니다.

통계량은 다음과 같은 수식입니다.

분자가 음수여야만 시계열이 정상 상태일 때입니다. 실제로는, 여러 라이브러리에서 ADF 테스트를 계산할 수 있기 때문에 구현할 필요가 없어요. 아래 예시는 세 가지 시계열 데이터의 예시를 보여줍니다. 왼쪽은 AR(1) 프로세스를 참조하고, 가운데는 MA(1) 프로세스를 참조하며, 마지막은 AirPassenger 데이터셋을 사용합니다. 그래프 제목에는 프로세스 이름과 ADF 테스트의 p-값이 표시됩니다.

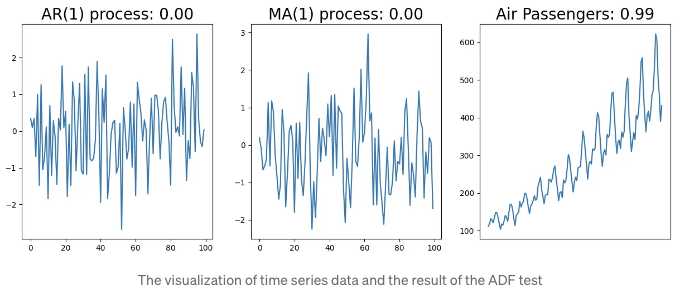
정상 데이터인 좌측과 가운데의 데이터는 임계값의 유의수준보다 작아서 귀무가설을 기각할 수 있어요. 이는 데이터가 정상 상태임을 의미해요. 반면에, 비정상 데이터인 우측은 임계값보다 더 유의미하기 때문에 귀무가설을 기각할 수 없어요. 이는 데이터가 정상 상태가 아님이라는 뜻입니다.

3.2 Durbin-Watson 테스트

Durbin-Watson 테스트는 시계열 회귀 모델의 잔차 항이 자기상관성을 갖고 있는지를 평가합니다. 이를 어떻게 활용할 수 있을까요? 다음과 같은 시계열을 사용하는 회귀 모델을 가정했을 때, 최소자승법을 사용하여 매개변수를 추정할 수 있습니다.

만약 Uₜ가 백색 잡음을 따르지 않는다면, 모델의 품질이 좋지 않을 수 있습니다. Uₜ에 일부 자기상관 또는 연속 상관이 있다고 생각할 여지가 있으며, 이를 모델에 포함해야 합니다. 이를 확인하기 위해 Durbin-Watson 테스트를 사용할 수 있습니다. Durbin-Watson 테스트는 잔차 항이 AR(1) 모델을 가정합니다.

다음은 귀무가설과 대립가설을 설정합니다.

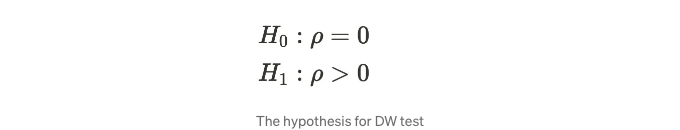
우리는 다음과 같은 Durbin-Watson 통계량을 사용합니다.

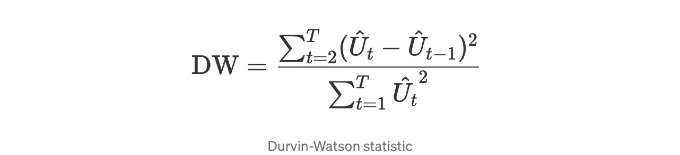
이 공식은 좀 더 직관적일 수 있습니다. 따라서 바꿔보겠습니다. 우리는 T가 다음과 같은 관계에 충분히 크다고 가정합니다.

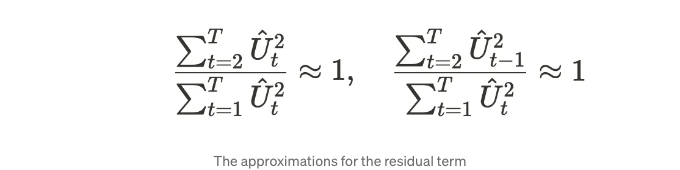
이러한 공식을 사용하여 Durbin-Watson 통계량을 다음과 같이 변환할 수 있습니다.

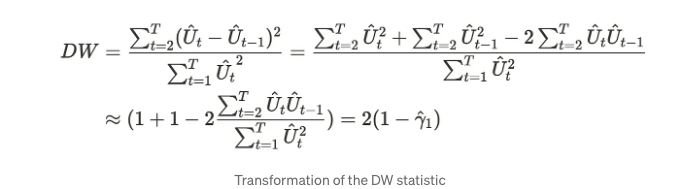
γ는 적자 순서 자기 상관 관계를 의미합니다. DW 통계량은 자기 상관 관계가 0에 가까울수록 2에 가까워지며, 이는 시계열에 거의 자기 상관 관계가 없음을 의미합니다. 반면, 시계열에 자기 상관 관계가 있는 경우 DW 통계량은 2보다 작아집니다.

섹션 2.4에서 생성한 ARIMA 모델을 사용하여 DW 통계량을 확인해보겠습니다.

from statsmodels.stats.stattools import durbin_watson

arima = pm.arima.ARIMA(order=(2,1,2))
arima.fit(y_train)

dw = durbin_watson(arima.resid())
print('DW 통계량: ', dw)
# DW 통계량:  1.6882339836228373

DW 통계량은 2보다 작기 때문에 자기상관 또는 연령상관성이 남아 있습니다. 아래 잔차 플롯을 보면 잔차에 여전히 일부 상관 관계가 있음을 알 수 있습니다.

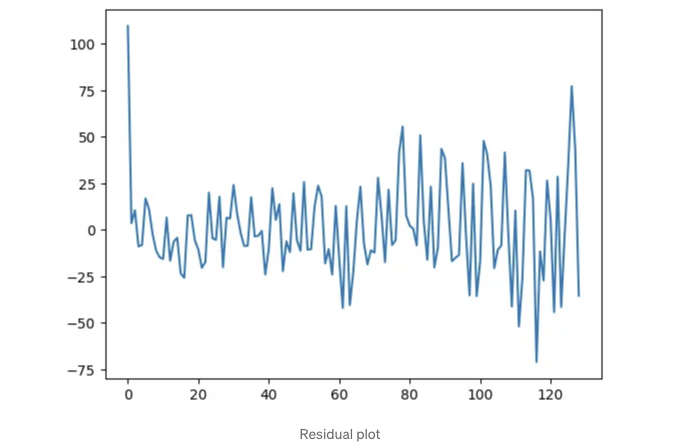
이 경우, 데이터를 올바르게 맞추기 위해 더 고급 모델을 사용해야 합니다. SARIMA, 반복 신경망, prophets 등을 사용할 수 있습니다.

이 블로그에서 결과를 생성하기 위해 아래 코드를 사용했습니다.

이 블로그의 끝입니다. 제 블로그를 읽어주셔서 감사합니다!

참고 자료

• 統計検定 準一級
• Wang, D., Lecture Notes, University of South Carolina

[3] Buteikis, A., 02 Stationary time series

[4] AirPassengers dataset, kaggle

[5] Eshel, G., The Yule Walker Equations for the AR coefficients

[6] Bartlett, P., Introduction to Time Series Analysis. Lecture 12, Berkeley university

[7] pmdarima: Python에서 사용할 수 있는 ARIMA 추정 도구