
가끔 우리는 유일한 확실한 것은 불확실함이라는 것을 듣습니다. 우리는 불확실성을 좋아하지 않습니다. "내일 날씨는 50% 폭염, 50% 허리케인일 것이다"라는 말을 듣고 싶지 않습니다. 그러나 반대로 불확실성을 양적으로 나타내기 위해 가능한 예측 범위를 요청하기도 합니다. 불확실성 속에서도 확실성을 원하는 건데요. 미래를 위해 계획을 세우는 데 도움을 주기 위해서입니다. 조직의 재정 계획을 수행 중이라고 상상해 봅시다. 두 가지 중 어느 것이 더 나을까요:
- 예상 평균 재정 손실은 4000만 달러이거나
- 재정 손실이 약 1000만 달러부터 7000만 달러 사이일 것으로 95% 확신하며, 약 4000만 달러 정도일 것입니다. 더불어, 재정 손실이 약 3000만 달러부터 5000만 달러 사이일 것으로 68% 확신합니다.
분위 회귀(Quantile regression)는 이 요구를 충족시킵니다. 분위 회귀는 예측 구간을 제공하며 표시된 것처럼 가능성을 양적으로 나타냅니다. 분위 회귀는 예측 변수와 반응 변수 간의 관계를 모델링하기 위해 사용되는 통계 기법으로, 반응 변수의 조건부 분포가 관심 대상인 경우에 특히 유용합니다. 예측 변수가 주어졌을 때 반응 변수의 조건부 평균을 추정하는 전통적인 회귀 방법(예: 최소 제곱 회귀)과 달리 분위 회귀는 반응 변수의 조건부 분위수를 추정합니다.
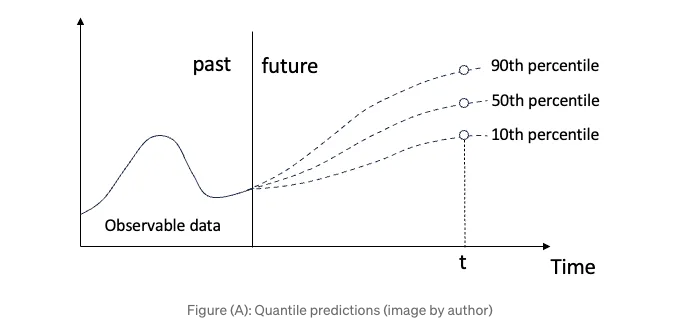
"Monte Carlo Simulation for Time Series Probabilistic Forecasts"에서 몬테카를로 시뮬레이션 기술을 배웠습니다. 양분위 회귀(Quantile regression)가 몬테카를로 시뮬레이션보다 어떤 장점을 가지고 있는지 알아보았습니다. 첫째로, 양분위 회귀는 예측 변수가 주어졌을 때 종속 변수의 조건부 양분위를 직접 추정합니다. 이는 몬테카를로 시뮬레이션에서와 같이 많은 가능한 결과를 생성하는 대신에 양분위 회귀는 종속 변수의 분포의 특정 양분위를 추정해줍니다. 이는 중앙값, 사분위 또는 극단적 양분위에서 예측 불확실성을 이해하는 데 특히 유용할 수 있습니다. 둘째로, 양분위 회귀는 예측 불확실성을 추정하기 위한 모델 기반 접근 방식을 제공합니다. 이는 관찰 데이터를 이용하여 변수 간의 관계를 추정하고, 이 관계를 기반으로 예측을 수행합니다. 반면에 몬테카를로 시뮬레이션은 입력 변수에 대한 확률 분포를 지정하고 무작위 샘플링을 통해 결과를 생성하는 데 의존합니다.
NeuralProphet를 사용하여 시계열 모델을 구축하는 방법을 다음 장(chapter)에서 배웠습니다:
- Chapter 3: Tutorial I: Trend + seasonality + holidays & events
- Chapter 4: Tutorial II: Trend + seasonality + holidays & events + auto-regressive (AR) + lagged regressors + future regressors
Neural Prophet은 두 가지 통계 기법을 제공합니다: (1) 분위수 회귀 및 (2) 일치 분위수 예측입니다. 일치 분위수 예측 기법은 회귀를 측정하기 위한 보정 프로세스를 추가합니다. 이 장에서는 Neural Prophet의 분위수 회귀 모듈을 실행할 것입니다. 다음 장에서 일치 분위수 예측을 배울 예정입니다. Python 노트북은 이 Github 링크를 통해 다운로드할 수 있습니다.
소프트웨어 요구 사항
NeuralProphet를 설치하기 위해 표준 설치 방법인 pip install NeuralProphet를 따를 것입니다.
!pip install neuralprophet
만약 Google Colab을 사용하는 경우, NeuralProphet은 numpy 1.23.5를 사용하지 않으면 작동하지 않는다는 점 유의해 주세요. numpy를 제거하고 numpy 1.23.5를 설치해야 합니다.
# neuralprophet은 numpy1.23.5를 사용하지 않으면 Colab에서 작동하지 않습니다: https://github.com/googlecolab/colabtools/issues/3752
!pip uninstall numpy
!pip install git+https://github.com/ourownstory/neural_prophet.git numpy==1.23.5
데이터를 로드하고, 몇 가지 도구를 가져와 보겠습니다:
%matplotlib inline
from matplotlib import pyplot as plt
import pandas as pd
import numpy as np
import logging
import warnings
logging.getLogger('prophet').setLevel(logging.ERROR)
warnings.filterwarnings("ignore")
이전 장에서 소개한 NeuralProphet을 계속 사용할 것입니다. Kaggle의 Bike Share Daily 데이터를 사용할 건데요 (여기나 여기서 다운로드 가능합니다). 이 데이터셋은 매일의 대여 수요와 온도, 풍속 등 다른 기상 정보가 있는 다중 변수 데이터셋입니다.
from google.colab import drive
drive.mount('/content/gdrive')
path = '/content/gdrive/My Drive/data/time_series'
data = pd.read_csv(path + '/bike_sharing_daily.csv')
data.tail()
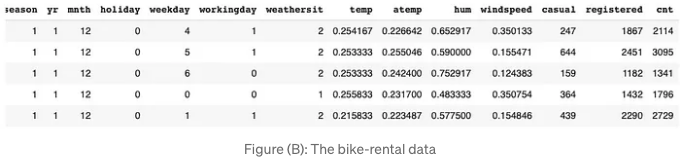
자전거 대여량을 그래프로 플롯해 봅시다. 두 번째 해에 수요가 증가하고 계절적 패턴이 있는 것을 관찰할 수 있어요.
# 문자열을 datetime64로 변환하기
data["ds"] = pd.to_datetime(data["dteday"])
# 대여량 데이터의 선 그래프 만들기
plt.plot(data['ds'], data["cnt"])
plt.xlabel("날짜")
plt.ylabel("수량")
plt.show()
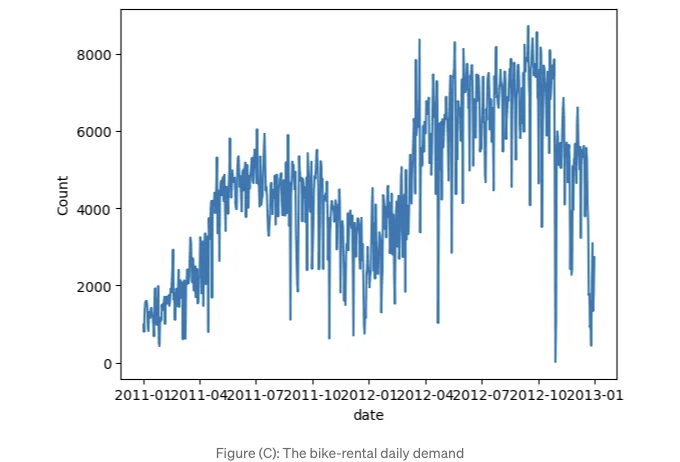
모델링을 위해 매우 기본적인 데이터 준비를 할 거에요. NeuralProphet에서는 칼럼 이름을 “ds”와 “y”로 지정해야 해요. Prophet과 동일하죠.
df = data[['ds','cnt']]
df.columns = ['ds','y']
지금부터 NeuralProphet에서 분위 회귀를 구축하러 바로 가봅시다. 5번, 10번, 50번, 90번, 95번 분위의 값을 얻고 싶다고 가정해봅시다. quantile_list = [0.05, 0.1, 0.5, 0.9, 0.95]로 지정하고, quantile_list를 켜려면 "parameter quantiles = quantile_list"를 사용합니다. 나머지 매개변수는 Chapter 3: Tutorial I: Trend + seasonality + holidays & events에서와 동일합니다.
from neuralprophet import NeuralProphet, set_log_level
quantile_list=[0.05,0.1,0.5,0.9,0.95]
# Model and prediction
m = NeuralProphet(
quantiles=quantile_list,
yearly_seasonality=True,
weekly_seasonality=True,
daily_seasonality=False
)
m = m.add_country_holidays("US")
m.set_plotting_backend("matplotlib") # Use matplotlib
df_train, df_test = m.split_df(df, valid_p=0.2)
metrics = m.fit(df_train, validation_df=df_test, progress="bar")
metrics.tail()
작업이 완료되면 prophet에서 상속받은 .make_future_dataframe()을 사용하여 예측을 위한 새 데이터 프레임을 만들 것입니다. n_historic_predictions 매개변수는 지난 100개 데이터 포인트만 포함하도록 설정됩니다. "True"로 설정하면 전체 기록이 포함됩니다. "periods=50"를 설정하여 다음 50개 데이터 포인트를 예측합니다.
미래 = m.make_future_dataframe(df, periods=50, n_historic_predictions=100) #, n_historic_predictions=1)
# 훈련된 모델로 예측 수행
예측 = m.predict(df=미래)
예측.tail(60)
예측값은 "forecast" 데이터 프레임에 저장됩니다.
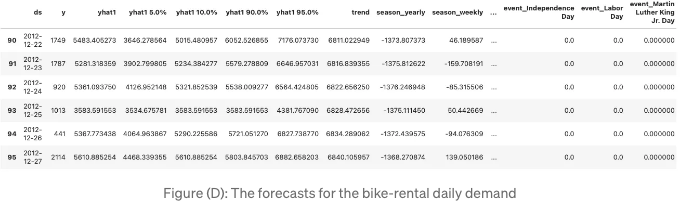
위 데이터 프레임은 플로팅을 위한 모든 데이터 요소를 갖고 있습니다.
m.plot(
forecast,
plotting_backend="plotly-static"
#plotting_backend = "matplotlib"
)
아래와 같이 플롯이 표시됩니다. 예측 구간은 분위값으로 제공됩니다!
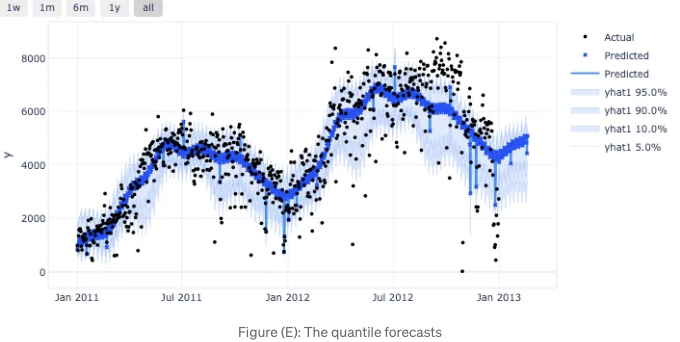
분위 회귀에 의한 예측 구간과 OLS에 의한 신뢰 구간은 다릅니다.
예측 구간이 인기를 얻으면, 분위수 회귀와 최소 자승법(OLS)에서의 신뢰 구간의 차이를 구별하는 것이 도움이 될 것입니다. 그림 (F)에서 좌측에는 선형 회귀를 그리고 우측에는 분위수 회귀를 표시했습니다.
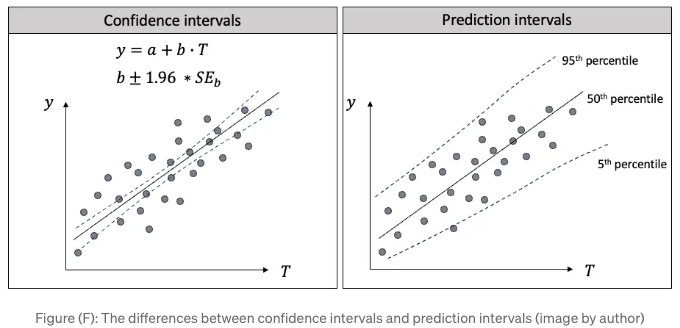
우선, 이들의 목표는 다릅니다:
- 선형 회귀: 주요 목표는 종속 변수의 조건부 평균과 가능한 한 가까운 예측 값을 찾는 것입니다.
- 분위수 회귀: 목표는 특정 신뢰 수준에서 예상되는 미래 관측값이 위치할 범위를 제공하는 것입니다. 종속 변수 Y의 조건부 분포의 다양한 분위수에서 독립 변수(T) 사이의 관련성을 추정합니다.
다음으로, 그들의 계산방법이 다릅니다:
- 선형 회귀에서 신뢰구간은 독립변수의 계수에 대한 구간 추정입니다. 예를 들어 b ± 1.96 * b의 표준 오차(Figure F)와 같이 표시됩니다. 이는 주로 최소 총 거리를 찾기 위해 최소제곱법(OLS)을 사용하여 데이터 포인트와 선 간의 거리를 최소화합니다. 계수가 변할 수 있기 때문에 예측된 조건부 평균값도 변할 수 있습니다. Figure F의 왼쪽 그래프에서, 계수 b가 변하기 때문에 예측된 평균값이 약간씩 다를 수 있습니다.
- 분위 회귀에서는 종속 변수의 25번째, 50번째 또는 75번째 분위와 같은 분위수 수준을 선택하여 회귀 계수를 추정합니다. 분위 회귀는 일반적으로 절대 편차의 가중 합을 최소화하지만 OLS를 사용하지는 않습니다.
세 번째로, 그들의 응용이 다릅니다:
- 선형 회귀에서는 "예측된 조건부 평균은 95% 신뢰구간 내에 있다"라고 말합니다. 신뢰구간은 전체 범위가 아닌 조건부 평균이기 때문에 예측 구간보다 좁습니다.
- 분위 회귀에서는 "예측값이 예측 구간의 범위 내에 들어갈 가능성이 95%입니다."라고 말합니다.
결론
이 장에서는 예측 구간을 위한 분위수 회귀의 개념을 배웠습니다. NeuralProphet을 사용하여 예측 구간을 생성하는 방법을 보여주었습니다. 또한 비즈니스 응용 프로그램에서 흔히 혼동되는 예측 구간과 신뢰 구간의 차이를 구별했습니다. 다음 장에서는 예측 불확실성에 대한 다른 중요한 기술인 준수 역분위 회귀(CQR)를 계속 공부할 것입니다.
샘플 eBook 장(무료): 링크
- 아름다운 형식으로 책을 재현하여 즐거운 독서 경험을 제공해준 The Innovation Press, LLC 직원들에게 감사드립니다. eBook을 분배하기 위해 Teachable 플랫폼을 선택했습니다. 이를 통해 부담스럽지 않은 경비와 전 세계 독자들에게 배포할 수 있었습니다. 신용카드 거래는 Teachable.com에서 기밀이지키며 안전하게 처리됩니다.
eBook on Teachable.com: $22.50 링크
The print edition on Amazon.com: $65 링크
- 프린트 판은 광택 처리된 표지, 컬러 출력물, 아름다운 Springer 글꼴 및 레이아웃을 채택하여 즐거운 독서 경험을 제공합니다. 7.5 x 9.25 인치의 크기는 서재에 있는 대부분의 책들과 어울립니다.
- “이 책은 부오파이의 시계열 분석에 대한 깊은 이해와 예측 분석 및 이상 감지 분야에서의 응용을 검증하는 것입니다. 이 책은 독자들이 실제 세상의 도전 과제에 대처할 수 있는 필수적인 기술을 제공합니다. 데이터 과학으로의 전환을 원하는 사람들에게 특히 가치 있는 자료입니다. 부오파이는 전통적인 기술과 최신 기술 모두에 대해 상세하게 탐구합니다. 부오파이는 신경망 및 기타 고급 알고리즘에 대한 토론을 통합하여 최신 트렌드와 발전 상황을 반영합니다. 이는 독자가 확립된 방법뿐만 아니라 데이터 과학 분야의 가장 최신 및 혁신적인 기술과도 상호작용할 준비가 되어 있는지를 보장합니다. 부오파이의 생생하고 접근 가능한 글쓰기 스타일 때문에 이 책의 명료함과 접근성은 높아졌습니다. 그는 복잡한 수학 및 통계 개념을 풀어내어 엄밀성을 희생하지 않으면서도 접근 가능하게 만들어냅니다.”
모던 시계열 예측: 예측 분석 및 이상 감지를 위한
Chapter 0: 서문
Chapter 1: 소개
Chapter 2: 비즈니스 예측을 위한 선지자
Chapter 3: 튜토리얼 I: 트렌드 + 계절성 + 휴일 및 이벤트
다음은 Markdown 형식으로 변경된 내용입니다:
-
Chapter 4: Tutorial II: Trend + seasonality + holidays & events + auto-regressive (AR) + lagged regressors + future regressors
-
Chapter 5: Change Point Detection in Time Series
-
Chapter 6: Monte Carlo Simulation for Time Series Probabilistic Forecasting
-
Chapter 7: Quantile Regression for Time Series Probabilistic Forecasting