TIL

Leetcode 200 섬의 개수 완벽 정복 가이드

Leetcode 200 섬의 개수 완벽 정복 가이드
TILPosted On Jul 9, 20245 min read

LeetCode의 "섬의 개수" 문제는 '1' (육지)과 '0' (물)로 구성된 m x n 그리드가 포함되어 있습니다. 이 문제는 그리드 내의 섬의 개수를 결정하는 것입니다. 여기서 섬은 수평 또는 수직으로 연결된 '1'의 그룹으로 정의되며, 물 ('0')로 완전히 둘러싸여 있습니다.

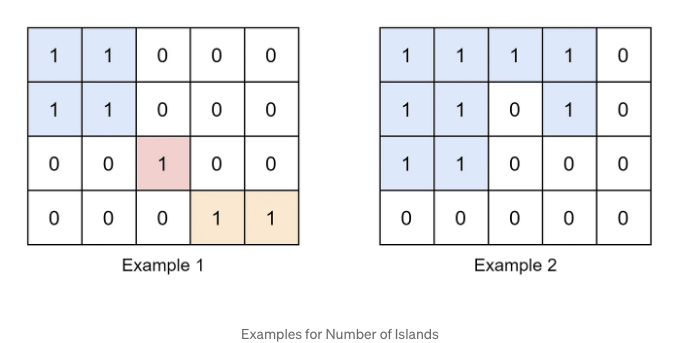
예를 들어, 예제 1에서는 총 3개의 섬이 있고, 예제 2에서는 하나의 섬이 있습니다. 중요한 점은 '1'들이 수평 또는 수직 연결을 통해서만 다른 '1'들에 연결될 수 있다는 것입니다.

그래서, 이 문제에 적합한 알고리즘은 무엇일까요?

이 문제는 그리드를 탐색하고 인접한 노드들을 체계적으로 탐색해야 하기 때문에 BFS가 가장 효율적인 알고리즘입니다. 그리드나 그래프 구조에서 연결된 구성 요소를 탐색하고 식별할 수 있는 능력은 이 작업에 잘 어울립니다.

BFS가 그리드에서 섬을 발견하는 방식을 시각화해 봅시다!

  • 알고리즘은 각 셀을 탐색하면서 그리드 안의 행과 열을 하나씩 탐색합니다.
  • 방문하지 않은 '1'로 표시된 셀을 탐색하기 위해 BFS를 사용합니다. 작업을 최적화하고 중복 방문을 피하기 위해 '방문함' 집합을 사용하여 이미 탐색한 노드를 추적합니다.
  • BFS는 방문해야 할 다음 노드를 유지하기 위해 큐도 필요합니다.

그림

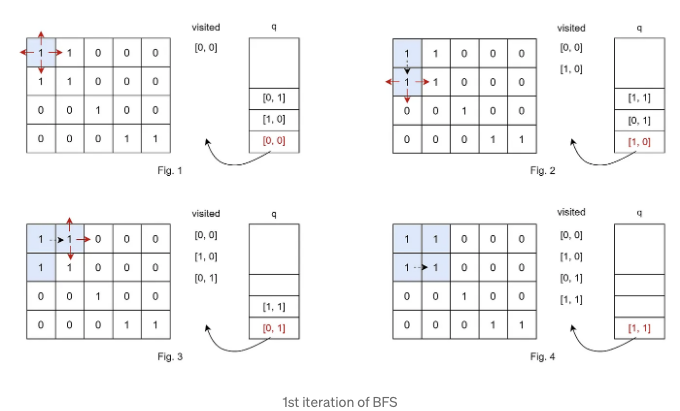
  • 셀 [0, 0]에서 탐사를 시작합니다. '1'이 포함되어 있기 때문에 섬의 일부로 간주되어 'visited' 세트에 추가됩니다. 이제 [0, 0]에서 4가지 방향으로 이동할 수 있습니다: [0, 1], [1, 0], [-1, 0], [0, -1]. 그리드를 벗어나지 않도록 하기 위해 [1, 0]과 [0, 1]만 남습니다. 이 두 셀은 현재 탐색 중인 동일한 섬의 일부라는 것을 나타내는 '1'입니다. 따라서 이러한 셀을 큐에 추가하여 다음에 방문합니다. (그림 1)
  • 다음으로 [1, 0]을 pop하고 visited 세트에 추가합니다. [1, 0]에서 4방향으로 갈 수 있습니다: [0, 0], [1, -1], [1, 1], [2, 0]. 그리드를 벗어나지 않기 때문에 [1, -1]을 버립니다. [0, 0]은 이미 방문했으므로 방문을 스킵합니다. [2, 0]은 '0'이므로 물이므로 방문할 필요가 없습니다. 방문되지 않은 [1, 1]은 '1'이므로 큐에 추가합니다. (그림 2)
  • '1'을 보면 새로운 셀을 큐에 추가하면서 계속해서 큐에서 셀을 탐색합니다. 현재 조사 중인 섬에 더 이상 탐색할 '1'이 없을 때까지 큐는 활성 상태를 유지합니다. 해당 섬을 완전히 탐색하면 그 섬에 대한 BFS가 중지됩니다. 한 섬을 완전히 탐사한 후에는 그리드에서 추가적인 섬이 있는지 검색합니다. (그림 3 및 그림 4)

그림

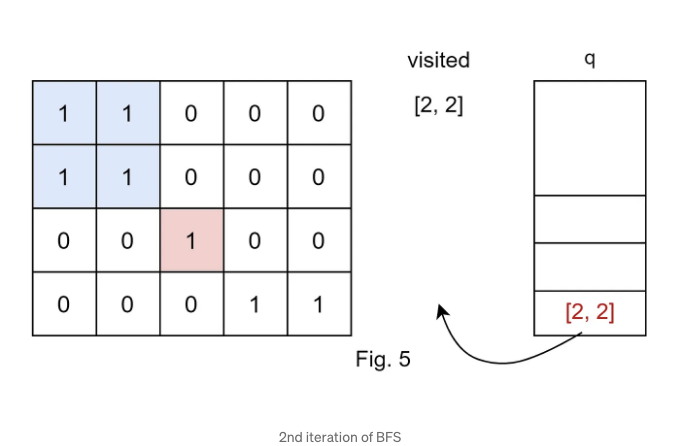
  • [2, 2] 셀의 경우 주변에 계속 탐색할 '1'이 없습니다. 이것은 다른 섬의 발견을 나타냅니다. 이 시점에서 큐가 비어 있으므로 다음 BFS 이터레이션으로 넘어갑니다.

그림

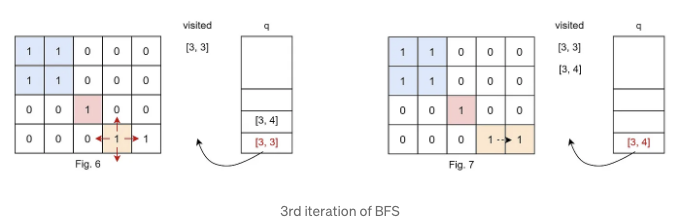
  • [3, 3]에 위치하면 [3, 4]로만 이동할 수 있습니다. 여전히 발견되지 않은 '1' 이므로 큐에 넣어줍니다.
  • [3, 4]를 팝하여 방문했다고 표시하고, 주변에 더 이상 발견되지 않은 '1'이 없기 때문에, 이 섬을 대상으로 하는 BFS 및 이후 알고리즘을 완료합니다.

따라서, 총 3개의 섬을 찾았습니다.

파이썬 구현:

import collections

class Solution(object):
 def numIslands(self, grid):

  if not grid:
   return 0

  islands = 0
  visited = set()
  rows, cols = len(grid), len(grid[0])
  directions = [[1, 0], [-1, 0], [0, 1], [0, -1]]

  def bfs(r, c):
   q = collections.deque()

   visited.add((r, c))
   q.append((r, c))

   while q:
    cur_r, cur_c = q.popleft()

    for dr, dc in directions:

     new_dr = cur_r + dr
     new_dc = cur_c + dc

     if (new_dr in range(rows) and new_dc in range(cols) and
      grid[new_dr][new_dc] == "1" and (new_dr, new_dc) not in visited):

      visited.add((new_dr, new_dc))
      q.append((new_dr, new_dc))

  for r in range(rows):
   for c in range(cols):
    if (grid[r][c] == "1" and
     (r, c) not in visited):
     bfs(r, c)
     islands += 1

  return islands

시간 복잡도:

그래서, m x n 그리드에서, 여기서 m은 행의 수를 나타내고 n은 열의 수를 나타냅니다. 이 알고리즘은 각 셀을 정확히 한 번씩 통과합니다. 따라서, 이 알고리즘의 전체 시간 복잡도는 O(m×n)입니다.

읽어 주셔서 감사합니다! 즐거운 코딩하세요!