소개
LoRa (Long Range) 변조는 저전력 소비로 장거리 데이터 전송이 가능하게 하는 무선 통신 기술로, 사물 인터넷(IoT) 응용 프로그램에 이상적입니다. 치르프 스프레드 스펙트럼(CSS) 기술을 활용하여, LoRa 변조는 신호를 넓은 주파수 범위에 퍼뜨려 간섭에 대한 저항성을 향상시키고 데이터 전송의 견고성을 향상시킵니다. 이 변조 방법은 다른 통신 기술이 장애물이나 소음으로 인해 어려움을 겪는 환경에서 특히 효과적입니다. 멀리 떨어진 네트워크를 구축하고 확장 가능한 IoT 네트워크를 지원하기 위해 장거리 기능과 최소한의 에너지 요구 사항을 결합한 LoRa 변조는 스마트 시티, 농업 모니터링 및 산업 자동화와 같은 응용 프로그램을 용이하게합니다.
매개변수 정의
코드의 첫 번째 섹션은 LoRa 조작에 사용되는 매개변수를 정의합니다. 대역폭 B는 125 kHz (125e3)로 설정되고 샘플링 주기 T는 대역폭의 역수로 계산됩니다. 즉, T = 1 / B 입니다. 확산 계수(SF)는 7로 정의되어 있으며 LoRa 변조를 위한 전형적인 값으로 7에서 12 사이의 값으로 변할 수 있습니다. 이 계수는 심볼 주기 T_s를 결정하며, T_s = (2*_SF) _ T로 계산됩니다. 이러한 매개변수는 LoRa 시스템에서 심볼의 시간적 행동과 전송 속도를 정의하는 데 필수적입니다.
import numpy as np
import matplotlib.pyplot as plt
# Parameters
B = 125e3 # (125 kHz) bandwidth
T = 1 / B # sampling period
SF = 7 # spreading factor {7,8,9,10,11,12}
T_s = (2**SF) * T # symbol period
심볼 계산
이 코드 부분에서, 일곱 개 요소로 구성된 비트 벡터 w가 Spreading Factor (SF) 값에 해당하는 값으로 정의됩니다. 그런 다음 벡터 w는 10진수 값으로 변환됩니다. 먼저 변수 symbol이 0으로 설정됩니다. 그런 다음, for 루프는 w 벡터의 각 비트를 반복하며, 각 비트를 해당하는 2**h 값(여기서 h는 비트 인덱스)으로 곱한 다음 결과를 symbol 변수에 추가합니다. 이 프로세스는 이진 벡터를 변조할 심볼을 나타내는 10진수 값으로 변환합니다. 이 계산은 LoRa 변조에 있어서 중요하며, 디지털 정보를 전송에 적합한 형식으로 변환합니다.
w = [1, 1, 0, 1, 0, 1, 1]
symbol = 0
for h in range(SF):
symbol += w[h] * (2**h)
시간 및 시간 인덱스 벡터 생성 및 Chirp 계산하기
코드의 세 번째 부분은 Chirp 신호를 생성하는 데 필요한 시간 벡터를 만듭니다. t 벡터는 np.linspace 함수를 사용하여 생성되며, 이 함수는 0부터 T_s까지 num 개의 동일 간격으로 나누어진 점을 생성합니다. 점의 개수 num은 int(T_s / T)로 계산되어 샘플링 주기 T에 따라 점이 적절히 간격을 두고 생성됩니다. 그다음, k 벡터는 np.arange를 사용하여 생성되는데, len(t)까지 0.01의 간격으로 동일하게 나뉜 값을 생성합니다. 그리고 Chirp 신호는 chirp = np.exp(1j _ 2 _ np.pi _ ((symbol + k) % (2SF)) / (2SF) _ k) 공식을 사용하여 계산됩니다. 여기서, 1j는 허수 단위를 나타냅니다.
t = np.linspace(start=0, stop=T_s, num=int(T_s / T))
k = np.arange(start=0, stop=len(t), step=0.01)
# Chirp 공식
chirp = np.exp(1j * 2 * np.pi * ((symbol + k) % (2**SF)) / (2**SF) * k)
Chirp 신호들의 플로팅
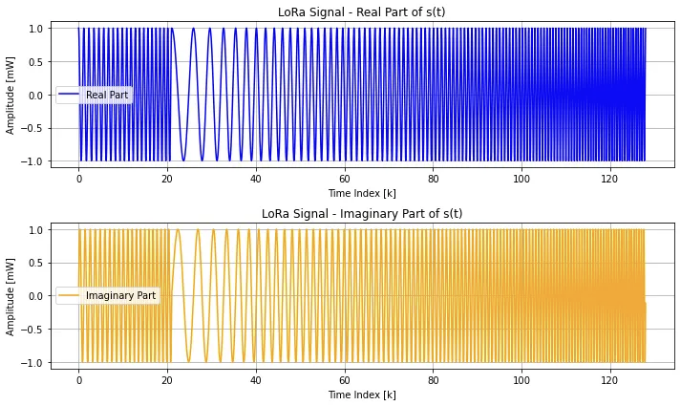
코드의 마지막 부분은 생성된 Chirp 신호를 시각화하는 부분입니다. 새로운 그림이 plt.figure(figsize=(10, 6))를 사용하여 10x6 인치 크기로 만들어집니다. Chirp 신호는 두 개의 서브플롯에 플로팅됩니다. 첫 번째 서브플롯(plt.subplot(2, 1, 1))은 plt.plot(k, chirp.real, label='실수부', color='blue') 함수를 사용하여 Chirp 신호의 실수부를 플로팅합니다. 제목, 축 레이블, 그리드 및 범례가 플롯에 추가되어 가독성과 데이터 해석이 향상됩니다. 두 번째 서브플롯(plt.subplot(2, 1, 2))은 plt.plot(k, chirp.imag, label='허수부', color='orange') 함수를 사용하여 Chirp 신호의 허수부를 플로팅하며, 마찬가지로 제목, 레이블, 그리드, 범례가 추가됩니다. 마지막으로 plt.tight_layout()은 서브플롯을 자동으로 조절하여 그림에 맞게 조절하고, plt.show()는 그림을 표시합니다. 이 시각화를 통해 Chirp 신호의 특성을 분석할 수 있습니다. 실수 및 허수부 모두를 통해 변조된 신호에 대한 완전한 이해를 제공합니다.
# Chirp 신호 플로팅
plt.figure(figsize=(10, 6))
# Chirp 실수부 플로팅
plt.subplot(2, 1, 1)
plt.plot(k, chirp.real, label='실수부', color='blue')
plt.title('LoRa 신호 - s(t)의 실수부')
plt.xlabel('시간 색인 [k]')
plt.ylabel('진폭 [mW]')
plt.grid(True)
plt.legend()
# Chirp 허수부 플로팅
plt.subplot(2, 1, 2)
plt.plot(k, chirp.imag, label='허수부', color='orange')
plt.title('LoRa 신호 - s(t)의 허수부')
plt.xlabel('시간 색인 [k]')
plt.ylabel('진폭 [mW]')
plt.grid(True)
plt.legend()
plt.tight_layout()
plt.show()
의견과 피드백은 댓글에서 환영합니다. 여기 테스트 용 전체 코드가 있습니다:
import numpy as np
import matplotlib.pyplot as plt
# Parameters
B = 125e3 # (125 kHz) 대역폭
T = 1 / B # 샘플링 주기
SF = 7 # 확산 계수 {7,8,9,10,11,12}
T_s = (2**SF) * T # 심볼 주기
w = [1, 1, 0, 1, 0, 1, 1]
symbol = 0
for h in range(SF):
symbol += w[h] * (2**h)
t = np.linspace(start=0, stop=T_s, num=int(T_s / T))
k = np.arange(start=0, stop=len(t), step=0.01)
# 칩 신호 공식
chirp = np.exp(1j * 2 * np.pi * ((symbol + k) % (2**SF)) / (2**SF) * k)
# 칩 신호 플롯
plt.figure(figsize=(10, 6))
# 칩의 실수부 플롯
plt.subplot(2, 1, 1)
plt.plot(k, chirp.real, label='실수부', color='blue')
plt.title('LoRa 신호 - s(t)의 실수부')
plt.xlabel('시간 인덱스 [k]')
plt.ylabel('진폭 [mW]')
plt.grid(True)
plt.legend()
# 칩의 허수부 플롯
plt.subplot(2, 1, 2)
plt.plot(k, chirp.imag, label='허수부', color='orange')
plt.title('LoRa 신호 - s(t)의 허수부')
plt.xlabel('시간 인덱스 [k]')
plt.ylabel('진폭 [mW]')
plt.grid(True)
plt.legend()
plt.tight_layout()
plt.show()
참고 자료
VANGELISTA, Lorenzo. Frequency shift chirp modulation: The LoRa modulation. IEEE signal processing letters, v. 24, n. 12, p. 1818–1821, 2017.