처음부터, Python에서

보간법은 데이터 과학자 뿐만 아니라 다양한 분야의 사람들에 의해 사용되는 매우 일반적인 수학적 개념입니다. 그러나 지리 공간 데이터를 다룰 때, 보간은 종종 희소한 관측치를 기반으로 대표적인 그리드를 만들어야 하기 때문에 더 복잡해집니다.

지리 공간 부분에 들어가기 전에, 선형 보간에 대해 간단히 되짚어 봅시다.

디자인을 보여드리기 위해 일반 다항 함수를 사용할 것입니다:

def F(x):
  return -2*x**3+x**2+2.1

x = np.arange(-5,5, 0.1)
y = F(x)

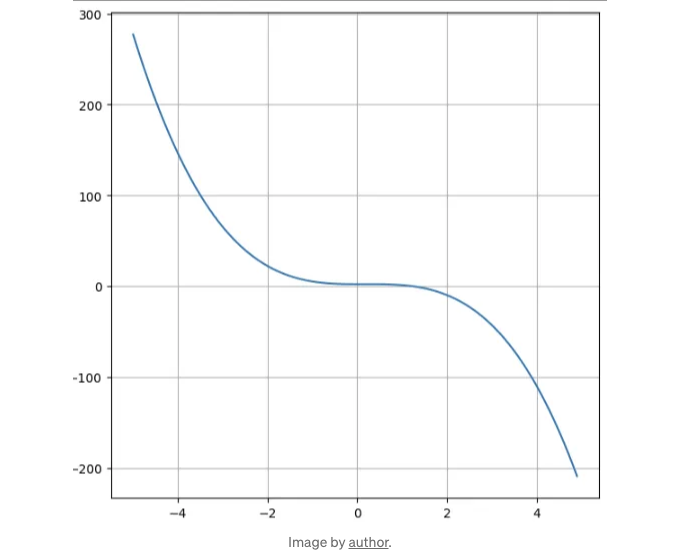
이제 [-4.2, 0, 2.5]에서 몇 개의 점을 무작위로 샘플링하고 이를 연결해 보겠습니다:

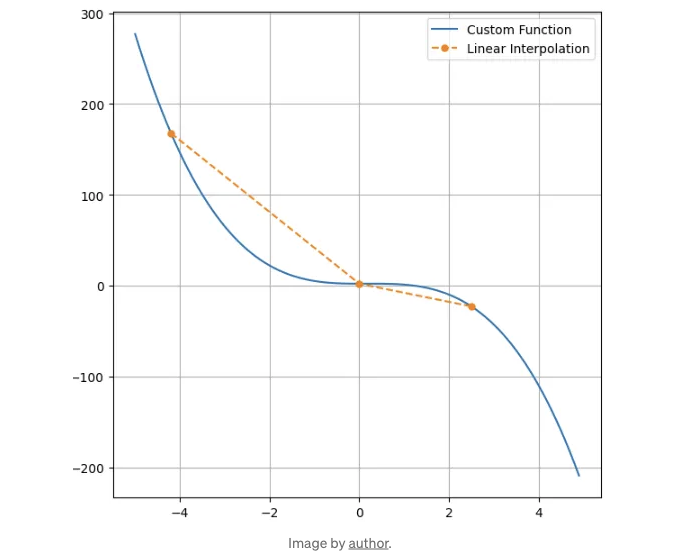
이것은 선형 보간법이라고 불립니다. 각 구간에서 직선으로 함수를 근사하고 있으며, 이제 3개의 점에서 함수의 값을 알고 있을 때 [-4.2;2.5] 구간 내의 값을 찾을 수 있습니다.

높은 정확도를 가진 많은 다른 방법들이 있지만, 그 뒤에 있는 아이디어는 동일합니다: 적어도 두 개의 알려진 점 사이에서 함수 값을 찾는 것입니다.

이제 지리 공간 부분으로 넘어갈 시간입니다. 이 자습서에서는 NOAA에서 제공한 스위스 전역의 기상 측정소에서 측정된 일일 평균 대기 온도의 공간 보간을 수행하는 것이 목표입니다. 기대되는 결과는 0.1° 해상도의 온도 그리드입니다.

먼저, 스위스의 행정 경계를 얻어와서 geopandas를 사용하여 시각화해야 합니다:

import geopandas as gpd

shape = gpd.read_file('gadm41_CHE_0.shp')
shape.plot()

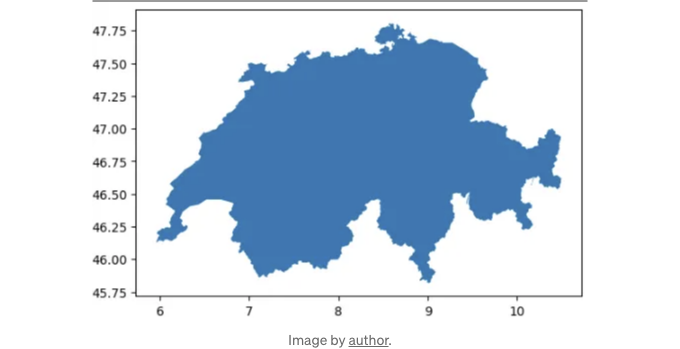
정말 대단해요! 스위스인 것 같네요 =)

이제 온도 관측치를 그래프로 표시하고 국가 모양과 겹쳐보겠습니다. 이를 위해 정기적인 판다 데이터프레임으로 기상 데이터를 로드한 다음 셰이프리 포인트로 변환한 지리 데이터프레임으로 변환하겠습니다:

import pandas as pd
from shapely.geometry import Point

df = pd.read_csv('3639866.csv')

points = list()
for i in range(len(df)):
  point = Point(df.loc[i, 'LONGITUDE'], df.loc[i, 'LATITUDE'])
  points.append(point)

gdf = gpd.GeoDataFrame(geometry=points).set_crs(shape.crs)

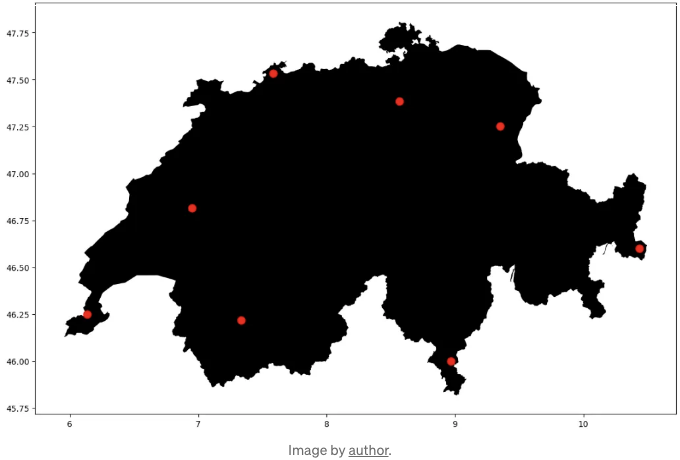
그렇게 하면 matplotlib을 사용하여 두 데이터프레임을 쉽게 겹쳐 볼 수 있습니다.

fig, ax = plt.subplots(figsize=(16,9))
shape.plot(ax=ax, color='black')
gdf.plot(ax=ax, color='r', markersize=85)
plt.show()

import matplotlib.ticker as mticker
import cartopy.crs as ccrs
from cartopy.mpl.gridliner import LONGITUDE_FORMATTER, LATITUDE_FORMATTER

LAT, LON = np.arange(45.75, 48, 0.1), np.arange(6, 10.81, 0.1)

fig, ax = plt.subplots(subplot_kw=dict(projection=ccrs.PlateCarree()), figsize=(16, 9))
shape.plot(ax=ax, color='grey')
gdf.plot(ax=ax, color='r', markersize=85)

gl = ax.gridlines(draw_labels=True,linewidth=2, color='black', alpha=0.5, linestyle='--')
gl.xlocator = mticker.FixedLocator(LON)
gl.ylocator = mticker.FixedLocator(LAT)
gl.xformatter = LONGITUDE_FORMATTER
gl.yformatter = LATITUDE_FORMATTER
plt.show()

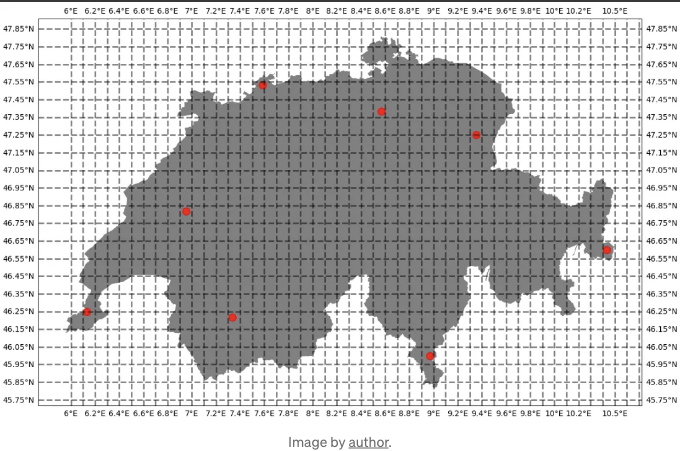
위 그림에 나타난 정규 그리드에 대해 보간을 수행하는 것이 목표입니다. 이 그리드에는 8개의 온도 관측치가 있습니다.

I. 최근접 이웃 (NN)

가장 직관적이고 간단한 방법 중 하나인 Nearest Neighbor (NN)에 대해 이야기하겠습니다. 이름에서 알 수 있듯이, 이 알고리즘은 각 그리드 노드에 가장 가까운 관측치의 값을 할당합니다.

이를 구현하기 위해 필요한 함수는 두 가지뿐입니다. 첫 번째 함수는 유클리드 함수이며, 다음 공식을 사용하여 두 점 사이의 거리를 계산합니다:

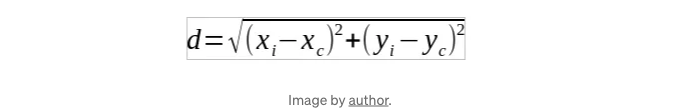
두 번째는 NN 메소드 자체입니다. 관측값을 저장할 빈 배열을 만든 후, 모든 위도와 경도를 반복하면서 각 포인트에서 현재 그리드 노드까지의 거리를 계산하고 그 그리드 노드에 가장 가까운 관측값을 할당합니다.

def 유클리드(x1, x2, y1, y2):
  return ((x1-x2)**2 + (y1-y2)**2) ** 0.5

def NN(data, LAT, LON):
  array = np.empty((LAT.shape[0], LON.shape[0]))

  for i, lat in enumerate(LAT):
    for j, lon in enumerate(LON):
      idx = data.apply(lambda row: 유클리드(row.LONGITUDE, lon, row.LATITUDE, lat), axis=1).argmin()
      array[i, j] = data.loc[idx, 'TAVG']
  return array

전체 아이디어는 이 한 줄에 있습니다.

idx = data.apply(lambda row: Euclidean(row.LONGITUDE, lon, row.LATITUDE, lat), axis=1).argmin()

변수 data는 각 행이 하나의 기상 장비 사이트를 나타내는 판다 데이터프레임입니다. 따라서 for 루프에서 거리를 계산하고 최소 거리를 가진 사이트의 인덱스를 찾습니다.

이제 알고리즘을 실행하고 결과를 xarray 데이터셋으로 래핑해 봅시다:

t2m = NN(df, LAT, LON)
ds = xr.Dataset(
    {'TAVG': (['lat', 'lon'], t2m)},
    coords={'lat': LAT, 'lon': LON})

이제 결과를 플로팅할 수 있습니다:

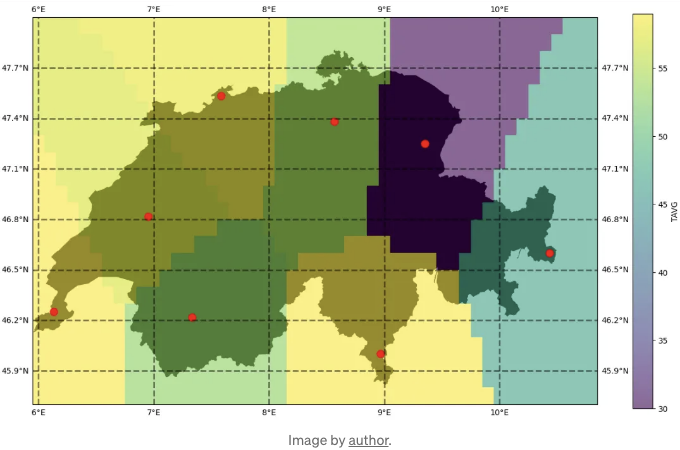
보기 좋지만, regionmask 라이브러리를 사용하여 스위스 매스크를 만들어 플롯을 더 보기 좋게 변경해 보겠습니다:

shape['new_column'] = 0
sw = shape.dissolve(by='new_column')['geometry']
rg = regionmask.mask_3D_geopandas(sw, lon_or_obj=ds.lon, lat=ds.lat)

fig, ax = plt.subplots(subplot_kw=dict(projection=ccrs.PlateCarree()), figsize=(16, 9))
#shape.plot(ax=ax, color='black')
ds.where(rg).TAVG.plot(ax=ax, alpha=0.6)
gdf.plot(ax=ax, color='r', markersize=85)
ax.gridlines(draw_labels=True, linewidth=2, color='black', alpha=0.5, linestyle='--')
plt.show()

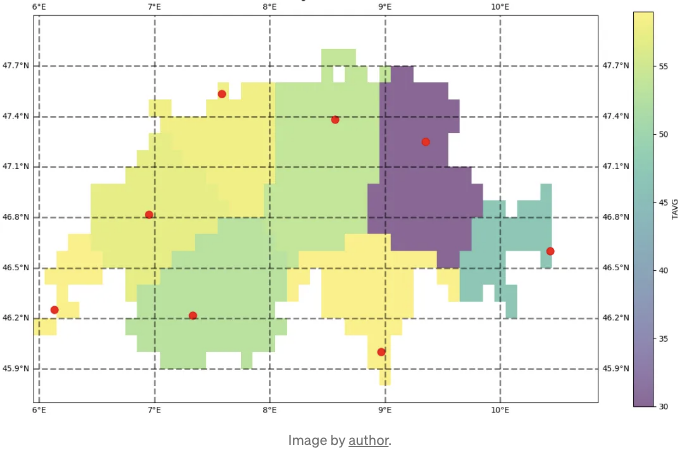
보시다시피 이 방법은 범주형 데이터에만 적용될 수 있습니다. 우리가 다루는 것은 온도로, 이는 연속 변수로 어떤 범위 안에서 어떤 값이든 가질 수 있다는 것을 의미합니다. 이 보간은 혼동스러울 수 있습니다. 현실에서는 항상 그라데이션과 무작위성이 있습니다.

그래서 좀 더 고급 알고리즘을 살펴보겠습니다.

II. 역 거리 가중 이동법 (IDW)

기본적으로 역 거리 가중치(IDW)는 NN의 향상된 버전입니다:

def IDW(data, LAT, LON, betta=2):
  array = np.empty((LAT.shape[0], LON.shape[0]))

  for i, lat in enumerate(LAT):
    for j, lon in enumerate(LON):
      weights = data.apply(lambda row: Euclidean(row.LONGITUDE, lon, row.LATITUDE, lat)**(-betta), axis=1)
      z = sum(weights*data.TAVG)/weights.sum()
      array[i,j] = z
  return array

가까운 알려진 점의 값을 할당하는 대신, 여기서는 가중치를 계산합니다. 그를 위해 앞서 언급한 유클리드 거리가 사용되지만, 이번에는 각 거리를 -β 승으로 제곱합니다 (β는 임의의 값입니다). 이러한 가중치는 각 지면 점이 특정 격자 노드에 미치는 기여를 나타냅니다. 거리가 멀수록 이 점이 노드 값에 미치는 영향이 적어집니다.

가중치를 얻은 후 가중 평균을 계산합니다.

Let’s plot it:

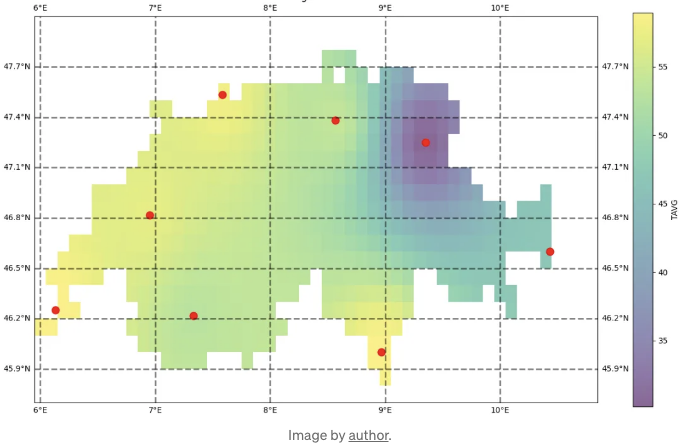
보시는 대로, 지금 결과가 훨씬 현실적이고 부드럽습니다!

III. 크리징

오늘의 마지막 메서드는 크리징입니다. 이 세 가지 방법 중에서 가장 복잡한 방법 중 하나이며, 우리는 간단히 알아볼 것입니다. 의식적이고 효과적으로 사용하고 싶다면 문헌을 살펴볼 것을 고려해보세요!

그러므로 이 방법의 주요 아이디어는 바리오그램(또는 세미바리오그램)을 사용하는 것입니다. 본질적으로 바리오그램은 어떤 매개변수의 변이가 거리와 방향에 따라 어떻게 변하는지를 측정합니다. 이것이 바로 우리가 공기 온도를 다룰 때 필요한 부분입니다.

크리징 알고리즘을 구현하려면 두 가지 유형의 변이로그램이 필요합니다: 실험적 변이로그램과 이론적 변이로그램입니다.

첫 번째는 정말 쉽게 계산할 수 있습니다. 감마 γ로 정의됩니다:

[ \gamma(h) = \frac{1}{2N(h)}\sum_{i=1}^{N(h)}[z(x_i) - z(x_i + h)]^2 ]

여기서,

• ( h )는 두 점 사이의 지리적 거리,
• (z)는 온도 함수입니다.

간단히 말해 이것은 알려진 점에서 온도 차이의 평균입니다.

이론적 변이그램은 다소 복잡합니다. 먼저, 그런것이 많이 있습니다:

여기서 p는 부분 재, d는 거리(h를 사용했었죠), n은 극소값, r은 범위를 나타냅니다.

CDT 콜롬비아에서 이러한 매개변수에 대한 정말 좋은 시각적 설명을 찾았어요. 저는 그들의 자료에서 γ와 거리 사이의 관계를 설명하는 이미지를 채택했습니다. 이제는 sill, partial sill, nugget 및 range가 무엇인지 명확해 보입니다.

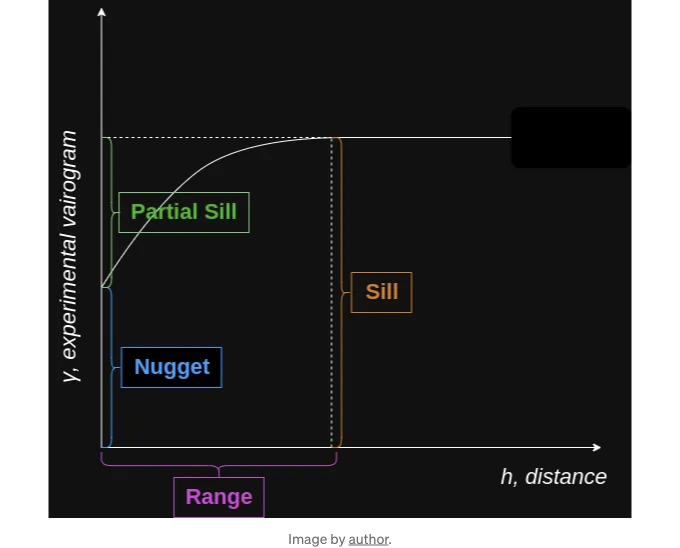
알고리즘의 전체 아이디어는 이론적 변이그램의 매개변수를 조정하여 실험적인 것에 맞게 맞추고, 그것을 사용하여 노드의 값을 예측하는 것입니다.

이 방법을 구현하려면 몇 가지 추가 라이브러리가 필요하며 OrdinaryKriging이라는 클래스를 생성해야합니다.

from scipy.linalg import solve
from itertools import product
from sklearn.metrics import mean_squared_error as MSE

class OrdinaryKriging:
    def __init__(self, lats, lons, values):
        self.lats = lats
        self.lons= lons
        self.values = values

        self.nugget_values = [0, 1, 2, 3, 4]
        self.sill_values = [1, 2, 3, 4, 5]
        self.range_values = [1, 2, 3, 4, 5]

        # 모수 값을 맞추기 위한 모든 조합 생성
        self.parameter_combinations = list(product(self.nugget_values, self.sill_values, self.range_values))
        self.optimal_pars = None

    def theoretical_variogram(self, h, nugget, sill, r):
        return nugget + (sill-nugget) * (1-np.exp(-3*h/r))

    def Euclidean(self, X, Y):
        all_dists, point_dists = [], []
        for x,y in zip(X, Y):
          k = 0
          for k in range(len(X)):
            h = np.linalg.norm(np.array([x, y]) - np.array([X[k], Y[k]))
            point_dists.append(h)
          all_dists.append(point_dists)
          point_dists = []
        return all_dists

    def gamma(self):
        distances = self.Euclidean(self.lats, self.lons)
        differences = np.abs(self.values.reshape(-1,1) - self.values)
        variogram_values = []
        for h in np.unique(distances):
            values_at_h = differences[(distances == h)]
            variogram_values.append(np.mean(values_at_h**2))
        return variogram_values, np.unique(distances)

    def fit(self):
        experimental_variogram, distances = self.gamma()
        fit_metrics = []
        for nugget, sill, range_ in self.parameter_combinations:
            theoretical_variogram_values = self.theoretical_variogram(distances, nugget, sill, range_)
            fit_metric = MSE(experimental_variogram, theoretical_variogram_values)
            fit_metrics.append((nugget, sill, range_, fit_metric))

        self.optimal_pars = min(fit_metrics, key=lambda x: x[3])[:3]

    def predict(self, point):
        points = np.array([(x,y) for x,y in zip(self.lats, self.lons)])
        distances = np.linalg.norm(points - point, axis=1)
        pars = list(self.optimal_pars)
        pars.insert(0, distances)
        weights = self.theoretical_variogram(*pars)
        weights /= np.sum(weights)
        return np.dot(weights, self.values)

kriging = OrdinaryKriging(df.LATITUDE.values, df.LONGITUDE.values, df.TAVG.values)

kriging.fit()

이제 각 함수를 따로 살펴봅시다. init 함수는 좌표와 값의 초기화 외에 nugget, sill, range의 가능한 값으로 구성된 세 개의 리스트를 포함합니다. 모든 가능한 조합으로 섞어서 parameter_combinations 변수에 저장됩니다. 우리는 나중에 최적 값을 찾을 때 필요할 것입니다.

def __init__(self, lats, lons, values):
        self.lats = lats
        self.lons= lons
        self.values = values

        self.nugget_values = [0, 1, 2, 3, 4]
        self.sill_values = [1, 2, 3, 4, 5]
        self.range_values = [1, 2, 3, 4, 5]

        # 맞추기 위한 모든 파라미터 값 조합 생성
        self.parameter_combinations = list(product(self.nugget_values, self.sill_values, self.range_values))
        self.optimal_pars = None

두 번째 함수인 theoretical_variogram은 이전에 언급된 공식 중 하나를 파이썬으로 구현한 것에 불과합니다. 여기서는 지수 함수입니다 (하지만 다른 함수에 대한 코드를 작성하여 결과를 비교할 수도 있습니다):

def theoretical_variogram(self, h, nugget, sill, r):
 return nugget + (sill-nugget) * (1-np.exp(-3*h/r))

세 번째 클래스 메서드는 유클리디안입니다. 이것은 NN과 IDW를 위해 만든 함수의 변경된 버전입니다. 이번에는 점과 모든 다른 점 사이의 거리를 나타내는 (n,n) 행렬을 반환합니다 (각 행에서 하나의 값은 0이며, 점과 그 자신 사이의 거리는 0입니다).

def Euclidean(self, X, Y):
        all_dists, point_dists = [], []
        for x, y in zip(X, Y):
          k = 0
          for k in range(len(X)):
            h = np.linalg.norm(np.array([x, y]) - np.array([X[k], Y[k]))
            point_dists.append(h)
          all_dists.append(point_dists)
          point_dists = []
        return all_dists

네 번째 함수는 fitting을 수행합니다. 여기서는 실험적 변리오그램 값과 유클리디안 거리를 얻습니다. 그런 다음 sill, range 및 nugget의 조합을 반복하면서 이론적 변리오그램 값과 실험적 값 사이의 평균 제곱 오차(Mean Squared Error, MSE) 추정을 계산합니다 (다른 메트릭을 사용할 수도 있습니다). 그런 다음 최적의 매개변수를 클래스 변수 optimal_pars에 저장합니다.

def fit(self):
        experimental_variogram, distances = self.gamma()
        fit_metrics = []
        for nugget, sill, range_ in self.parameter_combinations:
            theoretical_variogram_values = self.theoretical_variogram(distances, nugget, sill, range_)
            fit_metric = MSE(experimental_variogram, theoretical_variogram_values)
            fit_metrics.append((nugget, sill, range_, fit_metric))

        self.optimal_pars = min(fit_metrics, key=lambda x: x[3])[:3]

마지막으로 가장 중요한 함수는 예측입니다. 입력으로 점 (lat;lon)을 받아서 해당 점과 다른 알려진 값들 사이의 거리를 추정합니다. 그런 다음, 앞서 얻은 최적 파라미터를 전달하여 이론적 변이그램 함수를 호출하고 가중치를 출력값으로 받습니다. 그런 다음 가중 평균을 계산하고 반환합니다.

def predict(self, point):
        points = np.array([(x,y) for x,y in zip(self.lats, self.lons)])
        distances = np.linalg.norm(points - point, axis=1)
        pars = list(self.optimal_pars)
        pars.insert(0, distances)
        weights = self.theoretical_variogram(*pars)
        weights /= np.sum(weights)
        return np.dot(weights, self.values)

이제 모든 예측값을 수집하고 지도를 시각화할 수 있습니다:

row, grid = [], []
for lat in LAT:
  for lon in LON:
    row.append(kriging.predict(np.array([lat, lon])))
  grid.append(row)
  row=[]

ds = xr.Dataset(
    {'TAVG': (['lat', 'lon'], grid)},
    coords={'lat': LAT, 'lon': LON})

fig, ax = plt.subplots(subplot_kw=dict(projection=ccrs.PlateCarree()), figsize=(16, 9))
ds.where(rg).TAVG.plot(ax=ax, alpha=0.6)
gdf.plot(ax=ax, color='r', markersize=85)
ax.gridlines(draw_labels=True,linewidth=2, color='black', alpha=0.5, linestyle='--')
plt.show()

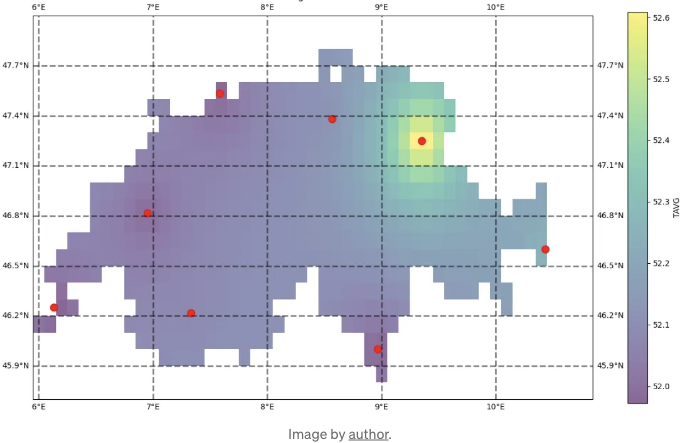
위와 같이 결과가 IDW에서 얻은 것과는 꽤 다르다는 것을 알 수 있어요. 크리깅에서 가장 중요한 매개변수는 선택한 이론적 변이그램 종류인데, 이는 사실 상 예측된 값과 거리 간의 관계를 정의합니다. 코드를 사용하기 귀찮으시거나 직접 작성하고 싶지 않다면 많은 변이그램 모델의 구현을 갖고 있는 PyKrige 라이브러리를 살펴보세요.

이 글이 유익하고 통찰력을 줬으면 좋겠어요!

저의 Medium에 올린 모든 게시물은 무료로 공개되어 있습니다. 그래서 여기서 제를 팔로우해 주실 경우 정말 감사하겠습니다!

참고로, 저는 (지리)데이터 과학, 기계학습/인공지능, 그리고 기후 변화에 대해 열정적으로 공부하고 있습니다. 만약 함께 프로젝트를 진행하고 싶다면 LinkedIn에서 연락 주세요.

🛰️더 많은 소식을 위해 팔로우 해주세요🛰️