파이썬 스크립트를 최적화하기 위해 PyTorch에 실망한 후 JAX를 사용하기 시작했습니다. 내 프로젝트는 주로 두 가지 주요 구성 요소로 이루어져 있었습니다: 원자 위치를 기반으로 설명자를 계산하고 이러한 설명자를 여러 신경망에 입력으로 사용하여 입자 시스템의 총 잠재 에너지와 힘을 예측하는 것이었습니다. 신경망 부분은 충분히 빠르지만, 특히 TorchScript를 사용한 후에도 설명자 계산, 특히 그래디언트 평가는 효율적으로 수행되지 않았습니다. 자동 미분을 지원하는 Python의 대체 프레임워크를 찾던 중 JAX를 발견했습니다. (물리학적인) 머신러닝 모델을 구축하는 데 매우 효과적이었고 필요한 유연성과 성능을 모두 제공했습니다.

PyTorch를 사용하는 데 이의를 제기하는 것은 없습니다. 사실, 자주 사용하여 언어 처리나 객체 탐지 작업을 포함한 머신러닝 모델을 구축할 때 사용합니다. 그러나 Python에서 사용자 정의 및 최적화된 모델을 개발하려는 경우, 아마도 PyTorch가 가장 적합한 선택이 아닐 수도 있습니다. PyTorch는 여러 면에서 뛰어나지만 매우 사용자 정의 및 특정한 모델 아키텍처에 대해서는 성능이 좀 더 우수한 대안이 있을 수 있습니다.

JAX는 자동 미분(autodiff), Just-In-Time (JIT) 컴파일, GPU 가속 컴퓨팅 및 벡터화된 계산 지원을 포함한 제 요구 사항과 완벽하게 일치하는 기능 세트를 제공했습니다. 게다가 JAX는 기능적 프로그래밍 패러다임과 일치하는 방법으로 가변성을 처리합니다. 이 게시물을 통해 JAX를 사용한 제 경험을 공유하고 여러분이 자신의 프로젝트에 JAX를 탐구하고 활용할 동기부여를 제공하는 것이 제 목표입니다.

필수 패키지

이 가이드를 따라가려면 몇 가지 Python 패키지를 설치해야 합니다.

JAX: 파이썬의 고성능 수치 계산 라이브러리로, 자동 미분과 CPU 및 GPU에서 최적화된 실행을 제공합니다. 이 설치 지침을 따르세요.
ASE: 분자 시뮬레이션을 설정, 조작 및 분석하는 도구상자로, 계산재료과학 분야에서 널리 사용됩니다. 설치: $ pip install ase
Pantea: 나의 Python 패키지로, 현재 개발 중이며 분자 간 포텐셜을 위한 기계 학습 모델을 개발하는 데 사용됩니다. 설치: $ pip install pantea
NGLView (옵션): 분자 구조 및 궤적을 대화식으로 보기 위한 주피터 위젯입니다. 설치: conda install nglview -c conda-forge

JAX는 시스템의 GPU를 자동으로 사용하며, 이용할 수 없을 경우 CPU를 사용합니다. 또한 JAX_PLATFORM_NAME 환경 변수를 미리 조정하여 연산 장치를 수동으로 설정할 수 있습니다.

기본적으로 JAX는 플로트32 데이터 유형을 사용하며, 이는 싱글 포인트 정밀도를 나타냅니다. 그러나 과학 시뮬레이션에서는 높은 정확성을 위해 더블 정밀도 플로트64가 필요합니다. 개선된 계산 성능을 위해 가능한 한 낮은 정밀도를 선택하고 메모리 사용량을 줄이는 것이 권장됩니다(약 2배 정도).

다음 스크립트는 JAX를 구성하여 장치를 선택하고 더블 정밀도를 활성화하는 방법을 보여줍니다.

import os
os.environ["JAX_PLATFORM_NAME"] = "cpu"  # GPU 컴퓨팅 비활성화
os.environ["JAX_ENABLE_X64"] = "1"       # 더블 정밀도 활성화

import jax
...

간단한 예제의 경우 기본 float32 정밀도를 사용하지만 분자 동역학을 시연할 때는 더블 정밀도를 사용할 것입니다. 또한, 이 글에서 모든 계산은 명시적으로 다른 장치가 명시되지 않는 한 제 노트북의 GeForce MX130 GPU에서 실행됩니다.

위에서 안내한 단계를 따르면이 포스트에서 다룬 예제를 재현하는 데 필수 도구를 제공받을 수 있습니다. 시작해 봅시다!

JAX란 무엇인가요?

JAX는 JIT 컴파일, 가속 컴퓨팅 및 자동 미분을 통해 고성능 수치 계산을 가능하게 하는 배열지향 컴퓨테이션용 오픈 소스이자 구성 가능한 파이썬 라이브러리입니다. 머신 러닝, 최적화 및 과학 시뮬레이션과 같은 고성능 수치 계산을 위한 사용자가 익숙한 NumPy 구문을 사용하여 코드를 작성하면 자동으로 효율적으로 해당 코드를 GPU 및 TPU에서 실행할 수 있도록 변환해줍니다. 이는 계산이 많이 필요한 작업에 높은 효율성을 가지며 매우 적합합니다. 선형 대수 가속화 X(LAX)는 JAX 라이브러리 내에서 서브 모듈 역할을 하며 다양한 선형 대수 루틴의 최적화된 구현을 제공합니다. JAX 문서 페이지를 방문하여 자세한 내용을 확인하는 것을 강력히 권장하며 다양한 정보와 자원을 제공하는데 도움이 됩니다. 예를 들어 이 튜토리얼을 참조해보세요.

일부 사람들은 JAX를 단순히 멀티스레드 NumPy 라이브러리로 설명하지만, 저는 그렇지 않다고 주장합니다. 그 이상의 기능을 제공합니다. 후속 섹션에서는 제 프로젝트 개발에 중요한 역할을 한 JAX의 주요 기능 몇 가지를 소개하겠습니다.

I. JIT 컴파일

Just-In-Time (JIT) 컴파일은 코드를 런타임에 컴파일하는 방법으로, 미리 컴파일하는 것이 아니라 코드를 컴파일하는 방법입니다. 이로 인해 코드를 실행 중인 특정 시스템에 맞게 최적화할 수 있으며, 미리 컴파일된 코드보다 성능이 향상될 수 있습니다. Python 스크립트는 해석되는데, 즉, 코드가 Python 인터프리터에 의해 한 줄씩 읽히고 실행됩니다. 이는 각 코드 줄을 처리한 후 실행해야 하기 때문에 컴파일된 코드보다 느릴 수 있습니다.

이와 대조적인 JIT 컴파일은 Python 코드를 런타임에 기계 코드로 변환하므로 컴퓨터의 CPU에서 직접 실행할 수 있습니다. 이는 Python의 오버헤드를 효과적으로 제거하고 해석된 코드보다 성능을 향상시킬 수 있습니다. 배열을 입력으로 받아 결과를 반환하는 더미 커널 함수의 예를 살펴보겠습니다:

import jax.numpy as jnp

def kernel(x):
  """더미 커널 함수."""
  result = 0
  for i in range(10):
      result += i * jnp.sin(jnp.cos(x))
  return result.sum()

랜덤 입력 배열을 생성하고 JIT 컴파일 없이 구현된 함수 호출의 실행 시간을 측정해 봅시다.

import jax

x = jax.random.normal(jax.random.key(2024), shape=(100_000, ))
# Array([ 0.8188207 ,  0.70407075, -0.553007  , ..., -0.07251461,
#       -1.353674  , -0.21451078], dtype=float32)

%timeit kernel(x).block_until_ready()
2.34 ms ± 134 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)

%timeit은 Jupyter 노트북과 IPython에서 사용되는 매직 커맨드로, 코드 조각의 실행 시간을 측정하는 데 사용됩니다. 여러 번 코드를 실행하여 평균 실행 시간을 얻으며, 상당한 변동성을 고려하여 성능을 더 정확하게 측정합니다.

JAX는 비동기 디스패치를 사용하므로, JAX 배열에 block_until_ready() 메서드를 호출하면 해당 배열이 계산을 완료할 때까지 Python 프로그램 실행이 차단됩니다. 계산 시간의 마이크로 벤치마킹을 작성할 때 이것을 권장합니다.

보고된 결과인 2.34 ms ± 134 µs per loop은 각각 100번 실행되는 7회의 실행을 기반으로 한 루프 당 평균 소요 시간 및 표준 편차를 나타냅니다.

이제 이 함수의 JIT 컴파일된 버전(또는 데코레이터를 사용하여 적용할 수도 있음)을 생성하고, 이후에 실행 시간을 다시평가하겠습니다.

import jax

jitted_kernel = jax.jit(kernel)

# 웜업 호출
# jitted_kernel(x)

%timeit jitted_kernel(x).block_until_ready()
82.5 µs ± 1.9 µs per loop (mean ± std. dev. of 7 runs, 10,000 loops each)
속도 향상:  29배

JIT 함수에 대한 웜업 호출은 일반적으로 속도를 평가하기 전에 컴파일하고 최적화하는 목적으로 실행됩니다. 함수 구현이 직관적하기 때문에 이 단계를 생략했습니다.

컴파일된 함수는 JIT 컴파일을 통해 심각한 성능 향상을 이루며, 컴파일되지 않은 버전보다 29배 빠르게 실행됩니다. 이 JAX 기능은 고성능 Python 함수를 작성할 수 있도록 돕습니다.

II. 자동 미분

자동 미분은 함수의 도함수를 자동으로 계산하는 계산 기술입니다. 유한한 차이를 사용하여 도함수를 근사하는 수치 미분이나 표현식을 조작하여 도함수를 찾는 기호 미분과는 달리, 자동 미분은 미분을 정확하고 효율적으로 평가하기 위해 미적분의 연쇄 법칙을 체계적으로 적용합니다. 요즘에는 자동 미분이 PyTorch, TensorFlow 및 JAX와 같은 딥 러닝 프레임워크에서 중요한 역할을 합니다. 효율적인 기울기 계산을 가능하게 하기 때문에 기울기 하강과 같은 최적화 알고리즘에 필수적인 기울기의 효율적인 계산이 허용됩니다.

자동 미분은 JAX의 핵심 기능으로, 기울기를 계산하는 프로세스를 단순화하고 가속화합니다. JAX는 여러 가지 함수를 제공하여 미분을 수행하며, 가장 두드러진 함수는 입력 변수에 대한 스칼라 값 함수의 기울기를 계산하는 jax.grad입니다.

이전 예제 커널을 고려해 봅시다. jax.grad를 사용하여 다음 코드를 통해 간단히 각 입력에 대한 출력의 기울기를 계산할 수 있습니다.

import jax

gradient_kernel = jax.grad(kernel)

kernel(x)
# Array(2401043.5, dtype=float32)

gradient_kernel(x)
# Array([-25.491356 , -21.069756 ,  15.582619 , ...,   1.7687505,
#        42.92778  ,   5.35899  ], dtype=float32)

%timeit gradient_kernel(x).block_until_ready()
56.3 ms ± 7.11 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)

게다가, JAX의 조합 가능한 기능 덕분에 jax.grad를 jax.jit과 원활하게 결합하여 커널의 기울기를 자동으로 계산하는 최적화된 함수를 만들 수 있습니다. 이를 통해 JAX의 자동 미분 기능을 활용하여 효율적으로 그래디언트를 계산하는 동시에 JIT 컴파일을 통해 성능을 향상시킬 수 있습니다.

import jax

jitted_gradient_kernel = jax.jit(gradient_kernel)

%timeit jitted_gradient_kernel(x).block_until_ready()
192 µs ± 37.7 µs per loop (mean ± std. dev. of 7 runs, 1 loop each)

분자 시뮬레이션 맥락에서, 물리적 시스템 내 이차력은 총 포텐셜 에너지 함수의 그래디언트에서 얻어집니다. 이 관계는 자동 미분의 중요성을 강조하는데, 이를 통해 힘의 구성요소를 정확하고 효율적으로 계산할 수 있는 수단을 제공합니다. 자동 미분을 사용함으로써, 포텐셜 에너지 함수의 필요한 도함수를 정확하게 계산하여 힘의 구성요소가 고정밀로 결정되도록 할 수 있습니다.

III. 자동 벡터화

벡터화된 계산은 개별 요소가 아닌 전체 배열에 작업을 적용하는 과정을 말합니다. 이는 현대 CPU 및 GPU의 가능성 (즉, SIMD)을 활용하여 연산을 병렬로 수행함으로써 전통적인 루프 기반 접근법에 비해 실행 시간이 크게 단축됩니다. Python에서 효율적인 코드를 작성하기 위해서 대부분의 경우 루프 사용을 피하고 배열에 작용하는 범용 함수의 효율적인 구현에 의존해야 합니다. 제 경험 상, 숫자 Python으로 전환하면 사고 방식 변화가 필요할 수 있습니다. C/C++와 같은 저수준 프로그래밍 언어는 여러 개의 루프를 일반적으로 사용하나, 숫자 Python의 접근 방식은 루프를 피하고 논리를 벡터 함수로 변환하는 것이 강조됩니다. 벡터화된 계산을 활용하면 전체 성능이 크게 향상됩니다. NumPy는 함수와 벡터화된 계산을 통해 혜택을 얻으며, 실제로 이는 그 성능과 효율성의 핵심 요소 중 하나입니다.

jax.vmap 변환은 함수의 벡터화된 구현을 자동으로 생성하여 배열에 대해 함수를 병렬 및 효율적으로 적용하는 것을 쉽게 만듭니다. 또한 명시적인 루프가 필요 없어지므로 코드를 간소화시킵니다.

위의 예시를 통해 위치 벡터 배열 간의 거리를 계산하는 방법이 얼마나 중요한지 살펴보겠습니다. 원자들 간의 거리를 결정하는 것은 분자 시뮬레이션에서 잠재 에너지를 평가하는 데 필수적입니다. 두 개의 배열 x와 y가 있다고 가정해보겠습니다. 각각은 일련의 원자들을 위한 위치 벡터를 포함하고 있습니다. 두 배열 모두 차원이 (natoms, 3)인데, 여기서 natoms은 원자의 수를 나타내고 배열의 각 벡터는 원자의 3D 좌표를 포함합니다. 우리의 목표는 이러한 배열에서 각각의 벡터 쌍 간의 거리를 포착하는 거리 행렬을 계산하는 것입니다. 아래 함수는 두 입력 배열 간의 이러한 거리 행렬을 반환합니다:

import jax.numpy as jnp

def calculate_distances(x, y):
    distances = []
    nrows, _ = x.shape
    for i in range(nrows):
        distances_from_single_point = jnp.sqrt(((x[i] - y)**2).sum(axis=1))
        distances.append(distances_from_single_point)
    return jnp.array(distances)

여기서 배열 계산을 사용하여 배열 x에 있는 각 지점에서 배열 y의 모든 지점까지의 거리를 효율적으로 계산했습니다. 예를 들어, 브로드캐스트된 항목 x[i] — y를 사용하여 명시적인 루프 없이 요소별 뺄셈을 수행할 수 있어 계산 효율성과 명확성을 높였습니다.

이 프로세스는 JAX에서 자동적으로 효율적으로 vectorize될 수 있습니다. jax.vmap을 사용하면 입력 배열의 첫 번째 인덱스를 효율적으로 처리하도록 일관되게 작동하는 함수로 단일 특정 지점에서 작동하는 함수를 변환할 수 있습니다. 이러한 기능을 실행하기 위해 먼저 한 지점을 처리하는 함수를 정의한 다음 jax.vmap을 사용하여 입력 배열의 첫 번째 인덱스에 대해이 함수를 일괄 처리하도록 일반화하여 루프 없이 일괄 처리에 대한 효율적인 계산을 가능하게 합니다. 이 방식은 코드를 단순화하는 데 도움이 되며 빠른 실행을 위해 JAX의 최적화 기능을 활용합니다.

import jax

def calculate_distances_from_single_point(xi, y):
    return jnp.sqrt(((xi - y)**2).sum(axis=1))

vmapped_calculate_distances = jax.vmap(
calculate_distances_from_single_point,
in_axes=(0, None)
)

in_axes=(0, None)는 벡터화된 함수의 입력 축을 지정합니다. 이 경우 첫 번째 인자 (xi)가 첫 번째 축 (0)을 따라 매핑되고, 두 번째 인자 (y)는 변경되지 않습니다(None). 이것은 모든 연산에서 동일하게 유지됨을 나타냅니다.

두 구현 모두 동일한 결과를 생성합니다. 아래 단언문은 루프를 사용한 구현으로 계산된 거리와 벡터화된 구현으로 계산된 거리가 동일함을 보장합니다.

import jax

# shape=(natoms, dim)의 무작위 배열 생성
x = jax.random.normal(jax.random.key(2024), shape=(100, 3))

assert jnp.allclose(
  calculate_distances(x, x),
  calculate_distances_vmap(x, x)
)

그럼에도 불구하고, 매핑된 함수의 성능은 벡터화가 더 잘 되어있기 때문에 크게 향상되었습니다. 또한 구현이 더 읽기 쉽습니다. 시간 프로필링 결과는 다음과 같이 이러한 차이점을 분명히 보여줍니다:

%timeit calculate_distances(x, x).block_until_ready()
93.5 ms ± 6.04 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)
Speed up:  1x

%timeit vmapped_calculate_distances(x, x).block_until_ready()
2.54 ms ± 147 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
Speed up:  36x

우리는 이제 다시 JIT 컴파일을 jax.vmap과 결합하여 더 나은 성능을 달성할 수 있습니다.

jitted_vmapped_calculate_distances = jax.jit(vmapped_calculate_distances)

%timeit jitted_vmapped_calculate_distances(x, x).block_until_ready()
60.3 µs ± 1.59 µs per loop (mean ± std. dev. of 7 runs, 10,000 loops each)
Speed up: 1558x

이 조합은 JAX의 고급 최적화 기법을 최대한 활용하여 계산의 효율성을 극대화합니다. 이 글에서 이에 대해 논의하고자 합니다.

다음 섹션에서는 JAX가 실제 문제 해결과 파이썬에서 고성능 애플리케이션을 개발하는 믿을 수 있는 프레임워크가 될 수 있는 분자동역학 쇼케이스를 소개할 것입니다.

분자동역학 쇼케이스

문서에서 명확하고 명확하게 정의된 코드 예제는 종종 복잡한 문제에 대처할 때 단점이 됩니다. 더욱 심각한 문제와 상호작용하는 것은 항상 우리의 이해력을 향상시키고 최적화된 응용 프로그램을 개발하기 위해 고급 기능을 활용할 수 있게 만들어줍니다. 분자 시뮬레이션의 복잡한 세부 사항에 심취하지 않아도 이 쇼케이스가 도움이 되었으면 좋겠습니다. 그 세부 전문 지식을 요구하는 분야에 대한 이해를 강조하기 위해 간단한 원자 시스템에 초점을 맞추어 JAX 스크립트 최적화에 필요한 주요 기능을 강조하기로 결정했습니다. 이 예는 기본 도메인 지식에 대한 더 명확한 이해를 용이하게 하기 위해 일부러 단순하게 유지되었습니다.

MD 시뮬레이션이란?

분자동력학(MD) 시뮬레이션은 원자와 분자의 물리적 움직임을 연구하는 데 사용되는 강력한 계산 방법입니다. 이는 이러한 입자들의 움직임을 시뮬레이션하여 복잡한 시스템의 물리적 및 화학적 특성에 대한 세부적인 통찰력을 제공합니다. MD 시뮬레이션은 물리학, 화학, 재료과학과 같은 다양한 분야에서 널리 사용되며 실험적으로 포착하기 어려운 현상의 미시적인 관점을 제공합니다.

MD 시뮬레이션의 중요한 부분은 힘 필드(force field)입니다. 이는 분자 시스템의 잠재 에너지를 정의하는 수학적 함수와 매개 변수들의 모음입니다. 이는 원자들이 서로 상호작용하는 방식을 결정하며, 이들의 움직임을 이끄는 힘을 제공합니다. 원자들은 뉴턴의 운동 방정식에 따라 움직이며, 이는 입자의 위치와 속도가 어떻게 시간이 지남에 따라 변하는지를 설명하며, 그들에게 작용하는 힘에 반응합니다. Verlet 알고리즘은 뉴턴의 운동 방정식을 해결하기 위한 흔히 사용되는 수치 적분 방법입니다.

초기 구조

MD 시뮬레이션을 시작하려면 일반적으로 원자의 위치와 속도가 실험 구조나 무작위로 생성된 배열과 같은 특정 구성을 기반으로 초기화됩니다. 따라서 아래 코드는 ASE 패키지를 사용하여 헬륨 원자들의 간단한 입방격자 구조를 생성하고, JAX 배열에서 원자 좌표 및 관련 정보를 저장하는 컨테이너인 Pantea에 해당 구조를 만듭니다:

from ase import Atoms
from ase.visualize import view
from pantea.atoms import Structure

d = 6  # Angstrom 단위의 원자 간 거리
unit_cell = Atoms('He', positions=[(d/2, d/2, d/2)], cell=(d, d, d))
initial_structure = Structure.from_ase(unit_cell.repeat((10, 10, 10)))

view(atoms=initial_structure.to_ase(), viewer='ngl')

레너드-존스 힘장력

두 원자 간 상호 작용을 설명하기 위한 간단한 힘장 중 하나는 Lennard-Jones (LJ)입니다. 이는 약한 분자간 인력과 척력을 모델링하는 데 특히 유용합니다. 우리는 주어진 입력 구조에 대해 총 Lennard-Jones 포텐셜 에너지와 힘 성분을 계산하는 잠재 클래스를 정의해 보겠습니다.

import jax
import jax.numpy as jnp
from jax import Array
from pantea.atoms import Structure
from typing import NamedTuple, Optional

class LJPotentialParams(NamedTuple):
    epsilon: Array
    sigma: Array

class LJPotential:
    """Lennard-Jones 포텐셜의 간단한 구현입니다."""
    def __init__(
        self,
        sigma: float,
        epsilon: float,
        r_cutoff: float,
    ) -> None:
        self.sigma = jnp.array(sigma)
        self.epsilon = jnp.array(epsilon)
        self.r_cutoff = jnp.array(r_cutoff)
    def __call__(self, structure: Structure) -> Array:
        """총 포텐셜 에너지를 계산합니다."""
        return _compute_total_energy(
            LJPotentialParams(self.epsilon, self.sigma),
            structure.positions,
            structure.lattice,
            self.r_cutoff,
        )
    def compute_forces(self, structure: Structure) -> Array:
        """모든 원자에 대한 힘 성분을 계산합니다."""
        return _compute_forces(
            LJPotentialParams(self.epsilon, self.sigma),
            structure.positions,
            structure.lattice,
            self.r_cutoff,
        )

LJPotentialParams는 Lennard-Jones 포텐셜을 위해 두 가지 필수 매개변수를 저장하는 네임드 튜플입니다.

LJPotential 클래스는 입력 구조를 가져와 필수 인자를 두 내부 커널 함수인 _compute_total_energy와 _compute_forces로 전달하여 원하는 물리적 양을 계산하고 반환하는 역할을 실제로 담당합니다.

여기서 흥미로운 부분은 JAX 기능을 활용하여 함수를 최적화하는 것입니다. 다음으로, 에너지와 힘 계산의 핵심인 커널에 대해 별도로 설명하겠습니다.

위치 에너지

이론 두 원자 간의 레너드-존스 포텐셜은 다음 방정식으로 정의됩니다:

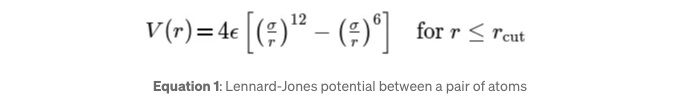
equation

V(r)은 두 입자 간의 거리 r의 함수로 표현되는 포텐셜 에너지이다. ε 매개변수는 인력의 강도를 나타내는 포텐셜 우물의 깊이를 의미한다. σ 매개변수는 상호작용하는 입자 간의 포텐셜이 제로가 되는 유한 거리로, 원자의 유효 지름을 나타낸다. 첫 번째 항은 보통 더 긴 범위에서 우세한 인력적 반 데르 발스 힘을 설명하고, 두 번째 항은 매우 짧은 거리에서 겹치는 전자 궤도 때문의 폴리 원자간 척반을 설명한다. rcut은 포텐셜이 제로로 간주되는 거리 범위를 나타내는 절단 반경이다. 일반적으로 상호작용 범위를 제한하여 효율성과 물리적 정확성을 향상시키기 위해 절단이 사용된다.

N 입자로 이루어진 시스템의 총 포텐셜 에너지 U는 모든 입자 쌍에 걸친 쌍별 상호작용의 합으로 다음과 같이 나타낼 수 있다:

[테이블 태그를 마크다운 형식으로 변경합니다.]

여기서, rij는 입자 i와 입자 j 사이의 거리이다. 각 입자 쌍이 한 번만 고려되도록 해야 하며 (중복 계산 없음), 자기 상호작용은 무시해야 한다.

구현 아래의 Python 코드는 원자 쌍 간의 Lennard-Jones 포텐셜 에너지를 계산하는 함수를 정의합니다.

def _compute_pair_energies(params: LJPotentialParams, r: Array) -> Array:
    term = params.sigma / r
    term6 = term**6
    return 4.0 * params.epsilon * term6 * (term6 - 1.0)

_compute_pair_energies 함수는 주어진 거리 (r)에 따른 원자 쌍의 Lennard-Jones 포텐셜 에너지를 계산합니다. 이 함수는 포텐셜 매개변수 (params)를 사용하고 계산 (식 1)을 수행하여 포텐셜 에너지의 배열을 반환합니다.

다음으로, 우리는 아래와 같이 원자 시스템의 총 Lennard-Jones 포텐셜 에너지를 계산하기 위한 JIT 컴파일된 함수를 정의합니다:

import jax
import jax.numpy as jnp
from pantea.atoms.neighbor import _calculate_masks_with_aux_from_structure

@jax.jit
def _compute_total_energy(
    params: LJPotentialParams,
    positions: Array,
    lattice: Optional[Array],
    r_cutoff: Array,
) -> Array:
    masks, (rij, _) = _calculate_masks_with_aux_from_structure(
        positions, r_cutoff, lattice
    )
    pair_energies = _compute_pair_energies(params, rij)
    pair_energies_inside_cutoff = jnp.where(masks, pair_energies, 0.0)
    return 0.5 * jnp.sum(pair_energies_inside_cutoff)

_calculate_masks_with_aux_from_structure 함수는 불리언 배열(masks)을 계산하여 각 원자 쌍이 cutoff 거리 내에 있는지를 나타내는데, 자기 상호작용은 제외됩니다. 또한 원자 쌍 간의 거리를 담은 배열(rij)을 반환하여, pair potential 평가를 위해 이 거리를 재계산하는 것을 피합니다. 이 함수는 Pantea에서 가져온 것이며, 이를 통해 토론을 간소화합니다. 거리를 계산하기 위해, 시뮬레이션 상자의 주기적 경계 조건(lattice)도 고려됩니다.

이전에 설명한 대로, _compute_pair_energies 함수는 잠재 에너지 매개변수와 거리(rij)를 사용하여 각 원자 쌍의 LJ 포텐셜 에너지를 계산합니다.

jnp.where는 masks를 적용하여 cutoff 거리 밖에 있는 원자 쌍에 대한 에너지를 0으로 설정하는 데 사용됩니다. 이 메서드는 루프를 사용하지 않고 배열에 조건부 논리를 효율적으로 적용합니다. np.where는 내부적으로 고도로 최적화된 C 코드로 구현되어 있습니다. 한꺼번에 전체 배열에 작용하여 벡터화된 작업을 수행할 수 있는 JAX의 능력을 활용합니다.

총 에너지는 jnp.sum을 사용하여 반환됩니다. 각 쌍의 상호 작용이 두 번 계산되기 때문에 0.5를 곱하여 계산합니다. 각 쌍이 두 번 고려되기 때문에 0.5를 곱해서 각 쌍의 상호 작용을 총 에너지로 계산합니다.

간단히 말해서 _compute_total_energy 함수는 원자 시스템의 전체 Lennard-Jones 포텐셜 에너지를 계산합니다. 먼저, 두 원자 쌍이 cutoff 거리 내에 있는지를 결정하기 위해 부울 마스크를 생성합니다. 그런 다음, rij를 사용하여 모든 쌍에 대한 레너드-존스 에너지를 계산하고, cutoff 내부의 쌍 에너지를 필터링하여 cutoff 거리를 고려한 쌍 에너지를 합산합니다. 이 함수는 원자 위치에 기초하여 총 상호 작용 에너지를 제공하는 MD 시뮬레이션에서 중요한 역할을 합니다.

원자별로 쌍 에너지를 계산해야 한다면 비효율적으로 보일 수 있습니다. 과거에는 이를 피하기 위해 if 문을 추가했지만, 이 구현에 비해 성능이 상당히 떨어지는 것을 발견했습니다. 이 구현은 벡터화된 계산을 사용하며, 전통적인 저수준 언어 접근 방식에서 벗어나 핵심 계산을 위해 배열 계산에 중점을 둘 필요가 있음을 강조합니다. C/C++로 모든 것을 최적화하려면 몇 일이 걸릴 수 있지만, Python의 이 방법을 통해 벡터화를 통해 훨씬 더 나은 성능을 달성하고 개발 시간을 크게 단축할 수 있습니다. 게다가, JAX 작업은 내부적으로 병렬화되어 있으며 실행 시간을 더 최적화하기 위해 여러 스레드를 활용합니다.

아래 예시 코드는 1000개의 원자를 포함하는 입력 구조체에 대한 총 포텐셜을 계산하는 방법과 예상 실행 시간을 보여줍니다:

ljpot(initial_structure)
# Array(-0.00114392, dtype=float64)

%timeit ljpot(initial_structure).block_until_ready()
5.12 ms ± 38.9 µs per loop (mean ± std. dev. of 7 runs, 100 loops each))

Force vector

이론 레너드-존스 시스템 내 두 입자 사이의 힘은 포텐셜 에너지에서 유도될 수 있습니다. i 입자에 대한 입자 j로 인한 힘 벡터 Fij는 레너드-존스 포텐셜 V(rij)의 음의 그래디언트로 주어집니다:

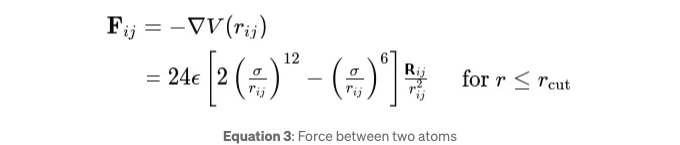
rij = ri — rj은 j 입자에서 i 입자를 가리키는 벡터를 나타냅니다. 우리는 힘에 대한 cutoff도 적용합니다. 입자 i에 작용하는 총 힘을 계산할 때, 다른 모든 입자 j로부터의 기여를 합산합니다:

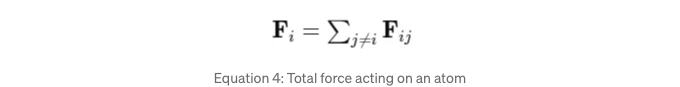
이는 시스템 내의 다른 모든 입자들로 인해 입자 i에 작용하는 순 힘을 제공하면서 자기 상호작용은 제외합니다.

구현 아래 코드는 Equation 3을 사용하여 원자 쌍 간의 힘을 계산합니다:

def _compute_pair_forces(params: LJPotentialParams, r: Array, R: Array) -> Array:
    term = params.sigma / r
    term6 = term**6
    coefficient = -24.0 * params.epsilon / (r * r) * term6 * (2.0 * term6 - 1.0)
    return jnp.expand_dims(coefficient, axis=-1) * R

_compute_pair_forces 함수는 레너드-존스 포텐셜을 사용하여 원자 쌍 간의 힘을 계산합니다. 이 함수는 잠재력 정의 매개변수, 원자 쌍 간의 거리 및 상대적인 위치 벡터를 입력으로 받습니다.

jnp.expand_dims(factor, axis=-1) * R: 상대적인 위치 벡터 R을 계산된 힘 인자로 확장하고, 곱셈 방송에 적합한 차원을 보장하기 위해 expand_dims를 사용합니다. 결과 배열은 각 원자 쌍 간의 힘을 나타냅니다.

다음으로, 우리는 다음과 같이 방정식 4를 사용하여 총 힘을 계산합니다:

@jax.jit
def _compute_forces(
    params: LJPotentialParams,
    positions: Array,
    lattice: Optional[Array],
    r_cutoff: Array,
) -> Array:
    masks, (rij, Rij) = _calculate_masks_with_aux_from_structure(
        positions, r_cutoff, lattice
    )
    pair_forces = _compute_pair_forces(params, rij, Rij)
    pair_forces_inside_cutoff = jnp.where(
        jnp.expand_dims(masks, axis=-1),
        pair_forces,
        jnp.zeros_like(Rij),
    )
    return jnp.sum(pair_forces_inside_cutoff, axis=1)

_compute_forces 함수는 최적화를 위해 JIT 컴파일로 각 원자에 작용하는 총 힘을 계산합니다.

_calculate_masks_with_aux_from_structure 함수는 cutoff 불리언 마스크를 계산하고 더불어 페어와이즈 거리 (rij) 및 상대적인 위치 벡터 (Rij)를 반환합니다.

jnp.where 함수는 마스크가 True일 때에만 계산된 페어 힘을 적용합니다. jnp.expand_dims(masks, axis=-1)는 브로드캐스팅을 위해 마스크 차원이 Rij와 일치하도록 합니다. 마스크가 False일 때는 0 힘 벡터를 할당합니다 (jnp.zeros_like(Rij)). 또한 JAX는 오버헤드를 줄이기 위해 메모리 풀을 사용하므로 제로 크기 벡터를 할당하는 것은 계산적으로 비용이 크지 않습니다. 배열에 대한 참조 재할당은 OS로부터 실제 메모리 할당이 포함되지 않기 때문입니다.

마지막으로, jnp.sum(pair_forces, axis=1)를 반환하면 각 원자에 작용하는 총 힘을 계산하여 모든 다른 원자를 고려합니다.

상자 내 모든 원자의 힘 구성 요소를 계산하고 실행 시간을 측정하는 유사한 예제 코드:

ljpot.compute_forces(initial_structure)
# Array([[ 1.11173074e-21,  1.11173074e-21,  1.11173074e-21],
#       ...,
#       [-1.87935435e-21, -1.87935435e-21, -1.87935435e-21]],  dtype=float64)

%timeit ljpot.compute_forces(initial_structure).block_until_ready()
6.71 ms ± 4.63 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)

지금까지 잘 진행되고 있어요! 여기까지 우리는 MD 시뮬레이션에 필요한 Lennard-Jones 포텐셜의 JAX 버전을 구현했습니다. 다음 단계는 이 포텐셜과 초기 구조를 사용하여 시스템을 시간에 따라 시뮬레이션하는 것입니다.

분자동력학 시뮬레이션

시스템을 시뮬레이션하기 위해 Pantea에 있는 MDSimulator 모듈을 사용합니다. 이 모듈은 시뮬레이션이 어떻게 진행될지를 정의하며, 적분 알고리즘, 열장치 및 필요한 기타 시뮬레이션 설정을 포함합니다. 시스템을 일정한 온도에서 시뮬레이션하므로 온도조절기를 정의하는 것이 필요합니다.

다음 매개변수를 사용하여 MD 시뮬레이터를 초기화해 봅시다:

from pantea.simulation import MDSimulator, BrendsenThermostat

time_step = 0.5 * units.FROM_FEMTO_SECOND      # 0.5e-15 초
thermostat = BrendsenThermostat(               # 온도 제어
  target_temperature=300.0,                    # 26도의 상온
  time_constant=100 * time_step                # 온도 조절 속도
)
simulator = MDSimulator(time_step, thermostat)

다음으로, 우리는 사실 원자들과 그들 사이의 상호 작용을 단순히 표현한 시스템을 만들 것입니다. 이 시스템은 원자의 위치, 속도, 그리고 상호 작용 매개 변수와 같은 정보를 포함합니다. 입력 구조로부터 시스템을 다음과 같이 생성할 수 있습니다:

from pantea.simulation import System

system = System.from_structure(
  initial_structure,   # 원자의 초기 위치
  potential=ljpot,     # 상호 작용을 LJ로 설정
  temperature=300.0    # 온도에 기반하여 원자 속도 초기화
)

마지막으로, MD 시뮬레이션을 실행하기 위해 simulate 함수를 호출합니다.

from pantea.simulation import simulate

# simulate(sys, simulator) # 워밍업 단계
simulate(system, simulator, num_steps=10000, output_freq=1000)

num_steps=10000: 이 매개변수는 수행할 총 시뮬레이션 단계의 수를 설정합니다. 각 단계는 일반적으로 시뮬레이션된 시간의 작은 증가에 해당하며 해당 기간 동안 원자의 위치와 속도가 업데이트됩니다.

output_freq=1000: 이 매개변수는 시뮬레이션 결과를 얼마나 자주 출력할지 지정합니다. 이 경우 데이터는 1000개의 시뮬레이션 단계마다 저장되거나 출력됩니다.

결과적으로 각 1000단계 후에 단계, 온도, 포텐셜 에너지 및 압력과 같은 물리적 특성을 출력합니다.

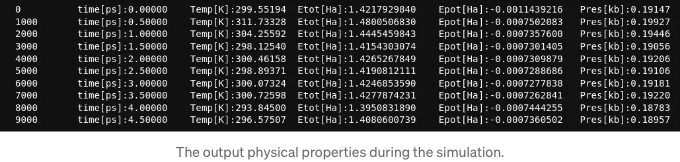
링크 텍스트

아래 그림은 주기 상자 내의 1000개 헬륨 원자를 사용한 MD 시뮬레이션의 시간 진화를 설명합니다:

성능 아래 그래프에서 볼 수 있듯이, 우리의 JAX 커널은 GPU (장치 1)의 거의 전체 용량을 효율적으로 활용하여 시뮬레이션을 수행합니다. 이 높은 수준의 자원 이용은 GPU의 계산 성능이 최대화되어 시뮬레이션의 속도와 성능이 크게 향상되는 것을 보장합니다.

저는 노트북 CPU와 더 강력한 GPU인 A100에서 동일한 MD 시뮬레이션을 수행했습니다. 결과는 GPU 계산으로 인한 상당한 속도 향상을 보여줍니다. GPU 하드웨어 사용의 중요성을 강조하기 위해 원자가 2000개인 시스템을 시뮬레이션했습니다. JAX의 훌륭한 기능 중 하나는 원본 코드를 수정하지 않고 CPU에서 GPU로 코드 실행을 원활하게 전환할 수 있다는 것이며, 이는 상당한 시간과 노력을 절약할 수 있습니다.

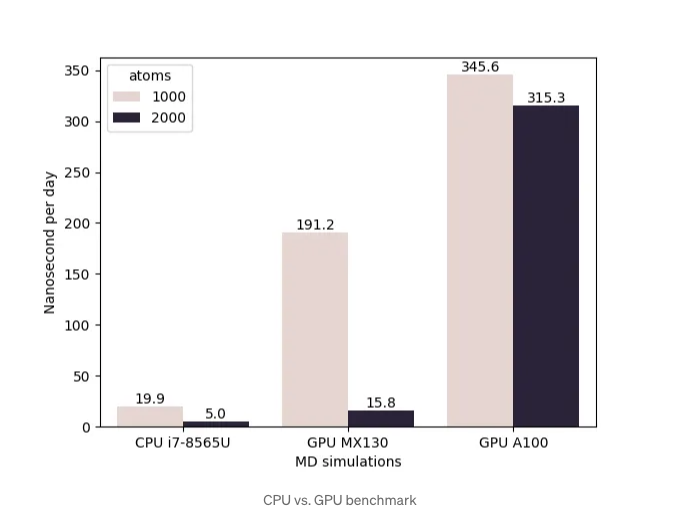
나노초당 일은 MD 시뮬레이션의 성능과 효율성을 나타내는 일반적인 측정 지표로, 시뮬레이션이 얼마나 빠르게 진행되는지를 보여줍니다. 그림에서 나타나듯이 GPU 가속 컴퓨팅은 코드의 성능을 수십 배 향상시킬 수 있습니다. 대규모 시뮬레이션의 경우, 도메인 분해를 사용하여 시스템을 병렬화하는 것이 최적의 접근 방식입니다. 이 방법을 사용하면 각 도메인은 제한된 GPU 메모리 요구 사항을 가지고 힘을 계산하고 원자 상태를 업데이트하는 데 사용할 수 있습니다.

마무리

이 게시물이 여러분의 호기심을 자극하고 JAX를 탐구하고 배우며 여러분의 프로젝트에 적용하는 데 도움이 되기를 바랍니다.

아래 링크된 저장소를 통해 JAX와 함께 하는 내 Pantea 프로젝트에 대해 더 알아보실 수 있습니다. 거기서는 JAX의 자동 미분 기능을 널리 활용하고 있습니다. 이 작업은 아직 진행 중이며 피드백이나 의견을 환영합니다.

읽어주셔서 감사합니다. JAX를 더 깊이 파고들어 작업에 최대한의 잠재력을 발휘하도록 장려합니다!

JAX를 배워야 하는 이유 분자동역학 적용 사례 소개